Curvelet变换是基于傅里叶变换和小波变换的一种改进,其特点是有高度的各向异性,具有良好表达图形沿边缘的信息的能力,对于恢复形状的沿边缘的主要结构和抑制周边噪声有其特有优势。
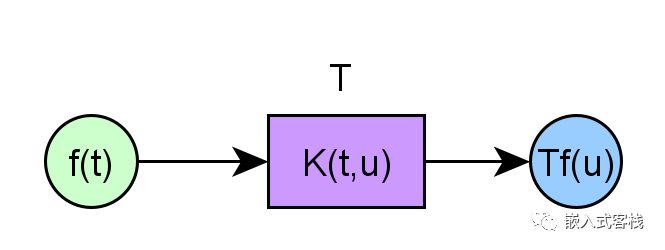
其过程为
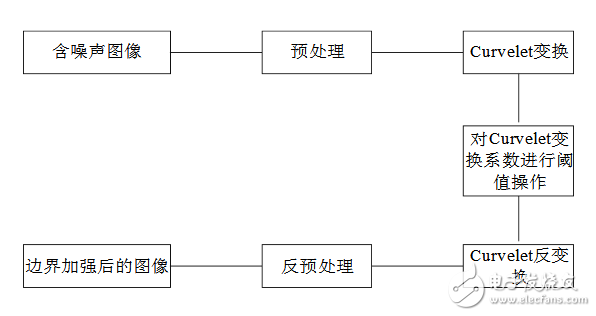
这和传统的DFT及小波变换的处理过程类似,把图表中的curvelet换成DFT和wavelet就可以了。
Curvelet变换是最近图像处理较新的一种多尺度几何变换算法。其发展历程在短短十年间:
1999年,Candès和Donoho在Ridgelet变换的基础上提出了连续曲波(Curvelet)变换——第一代Curvelet变换中的Curvelet99。
2002年,Strack、Candès和Donoho提出了第一代Curvelet变换中的Curvelet02。
2002年,Candès等人提出了第二代Curvelet变换。
2005年,Candès提出了两种基于第二代Curvelet变换理论的快速离散实现方法:
1)非均匀空间抽样的二维FFT算法(Unequally-Spaced Fast Fourier Transform,USFFT);
2)Wrap算法(Wrapping-Based Transform)
与小波变换类似,Curvelet变换同样有其对应公式。Curvelet系数可由下式得到,即信号与小波函数内积:
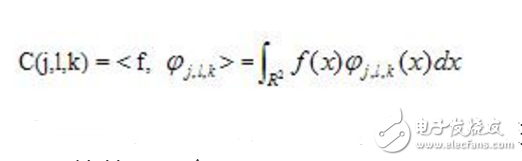
这里j表示尺度,l表示方向,k表示位移。变换的推导以及原理是个十分复杂的过程,这需要有相当强的数学功底。
Curvelet变换原理
Curvelet 变换通过对Radon 域内的每一个投影轴作一维小波分析,并由局部脊波分析得到多尺度结构。设参量θ是常数,平移量1是变量,脊波系数R,(a,b,θ)为


然后对每个分块用式(1,2)进行脊波分析。上面每步均可逆,经过逆变换可得重建图像。
通过Radon域的多角度投影,Curvelet变换明显加强了目标边界。同时由于Curvelet变换是多尺度脊波变换的子集,它可以用投影切片定理来实现:一幅n×n的图像可表达成2n条径向线的积分结果,对每条线的投影数据计算一维小波变换,就得到脊波系数。这样的Curvelet变换冗余因子达到16J+1。由于经典算法中分块的径向抽样角度恒定,直角坐标与极坐标的转换将导致在同一块内数据的非均匀抽样,当块中心附近的抽样值满足奈奎斯特抽样定理要求时,在块的边界部分将出现欠抽样;而当块边界部分满足抽样定理要求时,块中心部分数据将会过抽样,而且块的尺寸越大,非均匀抽样的影响就越明显。因此,在原算法中尽管离散Curvelet变换的实现较简单,但是为了无失真地重构图像,保证块边界周围的抽样值足够多,它在块的中心部分实施了过抽样,因此耗时和冗余度也相应增大。
 电子发烧友App
电子发烧友App














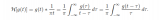













评论