前奏
19世纪的英帝国国力昌隆,在科学领域,英国同样也群星璀璨,在麦克斯韦震古烁今的电磁理论酝酿诞生的同时,查尔斯·巴贝奇(Charles Babbage)也在不断失败的处境中尝试着完成差分机和分析机,尽管至死都没有完成设备的组装和完整运行,但是,这些能够通过逻辑化的运作进行复杂数学运算的设备雏形却使得人们认识到通用计算机的可能性。
1936年,阿兰·图灵提出了现代计算机的概念。 (来源:NPL/Science Museum)
1936年,阿兰·图灵(Alan Turing)在论文《论数字计算在决断难题中的应用》(On Computable Numbers, with an Application to the Entscheidungsproblem)里提出了现代计算机的概念,天才的图灵是如此描述这样的设备的:“发明一台用来计算所有可计算数列的设备是完全可能的。”
1944年,世界上第一台电子数字可编程计算机巨人(Colossus)在英国问世,它的用途就是为了破解德军通信密码,在冷战期间,为了掩盖英国有能力破解洛伦兹密码机(Lorenz Cipher)的事实,丘吉尔下令销毁绝大部分巨人计算机。1946年,ENIAC在美国曝光,在战时,这台设备设计之初的主要目的就是来计算火炮射表,而它最早承担的项目还包括计算热核武器的可行性。
随着战争结束以及社会各行各业的复兴需求,体积庞大但在运算上有着惊人优势的计算机从战争期间的隐蔽战线开始越来越多地出现在民用和商业领域。
1951年,费朗替(Ferranti)公司为曼彻斯特大学开发出了世界上第一台商用计算机Ferranti Mark 1,同年,美国人口调查局采购了UNIVAC I,这是世界上第一台被大规模制造的计算机,仅仅3年之后,IBM 推出了“相对”而言更小更便宜的计算机IBM 650 ,这台设备净重超过900千克,算上电力供应装置之后则在1.35吨以上,售价高达50万美元或者每月租金为3500美元。
1947年,双体性晶体管问世,并逐渐取代真空管在以往计算机设计中的位置,1953年,世界上第一台可运行的晶体管计算机在英国问世,两年后,另一台包含200个晶体管、1300个固态二极管的晶体管计算机问世。相比真空管,晶体管的体积更小、耗能更少、更稳定而且寿命更长,但是最重要的是,它能容纳数以万计的逻辑电路。在1952年,集成电路概念首次被杰弗里·达莫(Geoffrey W.A. Dummer)提出,6年后,世界上第一个可运行的集成电路问世。晶体管和集成电路的出现意味着计算机有了更快的运行速度和更强大的计算能力。
1965年,英特尔联合创始人戈登·摩尔(Gordon Moore)在文章中提出了被后人补充进而成型的摩尔定律,10年后,摩尔本人再次对此定律做出调整:“在这10年末期,倾斜程度(半导体芯片上集成的晶体管和电阻数量)将每2年增加大约1倍。”
计算机的发展轨迹按照摩尔的预言波澜不惊地前行着,大众继续享受着计算机小型化、廉价化和性能提升带来的种种便利优势。但是,科学界却异常焦急,大量新的议题和项目迫切需要计算能力更加强大的计算机设备帮助,Altas、CDC6600、Cray 两代以及90年代面世的富士“数值风洞”(Numerical Wind Tunnel)、Hitachi SR2201等超级计算机尽管已经在一定程度上解决了科学家的需求,但是,他们对当时计算机的能力依然感到不满足而迫切地需要一种新的更加强大、速度更快的计算机设备。
匣中的失乐
数学上,算法是对函数进行有效计算的方法,算法研究的一个重要的切入点是寻找可以有效计算的函数,这类函数叫做递归函数。
1931年,哥德尔(Kurt Friedrich Gödel)提出并证明了后来被统称为哥德尔不完备定理的两条定理,而根据哥德尔不完备定理,一些函数在数学上是不能被算法计算的。
哥德尔对“计算”(computation)做出了清晰的定义,尽管在论文里这些定义看上去不尽相同,但它们最后都归于同一类可计算函数里。而邱奇-图灵假想(Church-Turning thesis)做出这样的判断,任何在算法上可计算的函数都能被图灵机计算。
计算机科学家把一个运行时间随着输入大小而像多项式展开那样增长的算法叫做“多项式时间”(polynomial-time),如果一个问题用多项式时间就能解决的话,大家就把它称作复杂类度为P的问题——绝大多数P类问题都用有效的算法解决,然而,大多数不属于P类的问题无论花多少时间也解决不了。
按照强邱奇-图灵假想(Strong Church-Turing Thesis)进一步推演的话,就是说,如果在物理计算机上计算一个可计算函数的时间是 T 的话,那么在图灵机上的时间则是O(Tc),而这里的常数 c 仅仅由计算机使用的函数类型决定。
随着数字计算机的出现,由于机器本身的容量和时间有限,这就使得可计算和不可计算之间的差别在计算机的实际应用上显得越来越重要,皮特·休尔(Peter Williston Shor)这样评价道,“如果所有计算机跑完一个可计算函数的时间里,太阳都燃烧殆尽了,这在实用方面可一点都不好。”
于是,一种新的迥异于传统算法的计算机呼之欲出。
1970年,斯蒂文·威斯纳(Steven Wiesner)就设想量子信息处理是解决密码逻辑认为较好的一种方式,这是量子计算最早的火花。在10多年后,在爱德华·福莱德金(Edward Fredkin)的可逆计算理念的启发下,费曼为大家开辟了那条新路。
费曼相信,一台基于量子力学现象的计算机在模仿量子力学现象上有着近水楼台先得月的先天优势。
“自然不是经典的,如果你想interwetten与威廉的赔率体系 自然的话,那你最好去用量子力学。”
在1982年发表的一篇论文中,诺贝尔奖得主费曼认为,在计算机上模拟量子力学内在地就需要指数级增长的投入,而他给出的建议则是,使用量子计算机。费曼相信,一台基于量子力学现象的计算机在模仿量子力学现象上有着近水楼台先得月的先天优势——早在1980年,保罗·贝尼奥夫(Paul Benioff)就在论文里提到了基于图灵机制造微量子力学系统计算机模型的可能性。
1985年,牛津大学的大卫·道勅(David Deutsch)在一篇论文里给出了量子计算的抽象模型,但是,此时大家的疑问还是,量子计算机究竟能解决哪些实际问题。7年后,道勅和理查德·约饶(Richard Jozsa)在论文里给出了他们的肯定答案:
“比起任何基于确定性算法的经典计算机,量子计算机在解决问题上所花的时间要少得多;比起任何基于随机算法的计算机的预期时间,量子计算机也相对更少。”
但是仅仅有量子计算机的设想还是远远不够的,没有算法支持的计算机无疑远远都只能停留在遐想阶段,要让所有人都真正信服量子计算机的巨大先进性,他们还需要更具说服力的事实。
正是从20世纪90年代开始,量子计算的研究取得了前所未有的丰硕成果,在各大公司实验室和院校机构的共同推动下,量子计算从科学家论文中的设想、算法逐渐落实到到实际制造的机器上。
1994年,贝尔实验室的休尔发表了论文,在里面向大家展示了他的量子算法分解大数的质因数的速度如何领先于当时的已知任何计算机——分解一个1000位的数字,传统计算机大约需要耗费10京(《孙子算经》载“万万曰亿,万万亿曰兆,万万兆曰京”)年的时间,而利用量子计算机的话,只需要20分钟左右。
休尔的量子算法将会对 RSA 等在内的加密算法和系统造成了显而易见的冲击,在此以前,破解一个 RSA 129位密码需要8个月时间以及1600名计算机用户,然而用量子算法破解 RSA 140位密码也只要数秒的时间而已。
休尔的发现使得量子计算机掀起了一场的风暴,不仅席卷了物理学和计算机科学领域,让他们感受到新的计算工具蕴含的巨大潜力,亦使得包括之前一直相信使用 RSA 算法的国家部门和各公司开始认真对待关注这个概念。
量子计算机第一次从科学家的象牙塔里走到了世人面前。
1995年,舒马赫(Benjamin Schumacher)发表了论文,第一次提出了量子比特信息学上的概念,并创造了“量子比特”(qubit)的说法。
比特(bit)是传统计算机中最基础的构件,它只存在两个状态0或1之间,在量子计算机中,情况却并非如此。量子力学告诉我们,量子具有叠加态的特性,因而,量子计算机中的比特——即量子比特——同时就有了0与1的状态,它既可以是1,亦可是0。基于量子平行,我们可以将这两种状态看成是处于两个不同宇宙里,那么,当一个量子比特进行运算时,实际上是处于两个宇宙里的数值在同时执行。
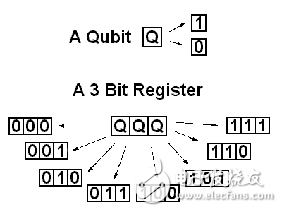
包含3个量子比特的寄存器
3个比特可以代表8种状态,但是寄存器却只能记录其中的一个结果,而3个量子比特构成的寄存器同时也具备了其线性叠加态效果,于是可以同时记录8种数值结果。通过这样一个简单的例子就能看出来量子计算机惊人的计算能力,是同数目(设为n)比特构成的经典计算机的2n倍。
理论上来说,一个量子比特可以储存的信息是无限的,当被测量时,状态满足一些特定条件的量子比特才会释出0或1那样的结果,也就是说,测量会使得量子比特从叠加态坍缩,反之,量子比特中存储的信息将始终处于动态演化过程之中,并且,通过量子门就能读取其中的信息。
假设我们取数字15来作为要分解的对象,设它作N,随机选一个数字设作X,并且1《X《N-1,将X当做寄存器A中内容的指数然后对N进行模除,余数则置于寄存器B中,即:

我们将这个运算结果列表如下:
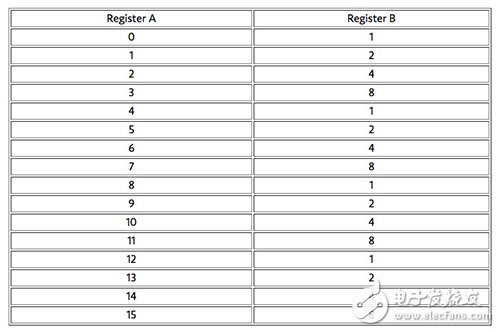
我们会发现上述取值的运算结果呈现出(1,2,4,8,1,2,4,8……)的重复数列,我们将重复的频次命为 f,那么这个运算中,f 的取值就是4。
通过寄存器B中一系列复杂的运算执行,上述的f可以在量子计算机中获得,得出的f值会带入下列公式计算出一个可能的因数。得出的结果不会一定就是正确的,但是生成f值的量子干涉会反复尝试对x进行代换从而筛选出正确的结果并排除错误的答案。

这就是休尔的量子算法的整体思路,它向科学界和大众真正展示了量子计算的强大威力。
计算机科学中一个最基本的问题就是非结构化搜索,1996年,贝尔实验室的拉夫·格罗夫(Lov Kumar Grover)在论文里提出了针对这一问题的量子算法。假设有 N 个黑箱,每个箱中包含确定的1或0,每次打开一个箱子记为一次搜索请求,那么如果我们想要寻找到包含1的箱子,那么最多讲需要进行N次请求,而格罗夫的算法则将其减少到了次。
量子计算机固然拥有众多优势,但是这些基于量子力学上的特性也使得它本身较之经典计算机更加不稳定。和经典计算机的设计、硬件并不一样,量子计算机的设计制造首先需要保证量子比特处于稳定的相干叠加态的之中。
量子计算机强大的能力是建立在量子相干态带来的量子平行上的,一旦相干态中的量子比特在和外部环境发生量子纠缠之后会陷入退相干状态,那么,此时的量子比特和传统比特一样只能表示一种状态,也就是说,不稳定状态下的量子计算机和经典计算机相比丧失了最大的优势——1995年,休尔和安德鲁·斯迪恩(Andrew Steane)分别独立发表了量子纠错的规划,试图以此来解决量子计算机在退相干上的隐患。
无论是休尔还是格罗夫的量子算法实际上都是建立在量子线路基础上的,而量子线路和经典计算机一样也包含导线——这里的导线在广义上还包括粒子、光子乃至地域传送、时间演化等——和逻辑门,前者用来传输信息,后者则负责操作。
 电子发烧友App
电子发烧友App




























评论