matlab概率统计实验
9.1 实验(I):Galton钉板试验
9.1.1 实验与观察: Galton钉板模型和二项分布
1. 动画interwetten与威廉的赔率体系
Calton钉板试验
【 rand('seed',1), u=rand(1,6) 】
【 rand('seed',2),u=rand(1,6) 】
观察程序zxy9_1.m
【 clear,clf, m=100;n=5;y0=2; %设置参数。
ballnum=zeros(1,n+1);
p=0.5;q=1-p;
for i=n+1:-1:1 %创建钉子的坐标x,y 。
x(i,1)=0.5*(n-i+1);y(i,1)=(n-i+1)+y0;
for j=2:i
x(i,j)=x(i,1)+(j-1)*1;y(i,j)=y(i,1);
end
end
mm=moviein(m); % 动画开始,模拟小球下落路径。
for i=1:m
s=rand(1,n); %产生n个随机数。
xi=x(1,1);yi=y(1,1);k=1;l=1; % 小球遇到第一个钉子。
for j=1:n
plot(x(1:n,:),y(1:n,:),'o',x(n+1,:),y(n+1,:),'.-'), % 画钉子的位置 。
axis([-2 n+2 0 y0+n+1]),hold on
k=k+1; % 小球下落一格 。
if s(j)>p
l=l+0; %小球左移 。
else
l=l+1; %小球右移 。
end
xt=x(k,l);yt=y(k,l); %小球下落点的坐标。
h=plot([xi,xt],[yi,yt]);axis([-2 n+2 0 y0+n+1]) %画小球运动轨迹。
xi=xt;yi=yt;
end
ballnum(l)=ballnum(l)+1; %计数。
ballnum1=3*ballnum./m;
bar([0:n],ballnum1),axis([-2 n+2 0 y0+n+1]) %画各格子的频率 。
mm(i)=getframe; %存储动画数据。
hold off
end
movie(mm,1) %播放动画1次。 】
2. 用二项分布描述Galton钉板模型
【 X = binornd(5,0.5,1,10) 】
3. 数学期望和平均收益
【 n=5;p=0.5; m=5000;
rand('seed',5); R = binornd(n,p,1,m); %模拟投球。
f=[5, 1, 0.2, 0.2, 1, 5]; %奖品的价值向量。
s=[];
for k=1:n+1 %计算第0~n格奖品价值。
u=[];
u=find(R==(k-1)); %计算落入第k-1格的小球下标,并存于向量u中。
s=[f(k)*length(u),s]; %计算相应的奖品价值,并存于向量s中。
end
mean_return=sum(s)/m %计算一次抽奖的平均回报 。 】
{ mean_return = 0.7506 }
【 f=[5, 1, 0.2, 0.2, 1, 5]; x=[0:1:n]; pu=binopdf(x,n,p);EF=sum(f.*pu) 】
9.1.2 应用、思考和练习
1. 二项分布的应用模型
◆电力供应问题 。
提示:
【 x=linspace(90,160,10); r = binornd(200,0.6,1,960); hist(r,x) ;
[n,x]=hist(r,x); 】
◆ 废品问题。
下面的程序可作为参考 。
【 clear,clf ,n=50;r=linspace(0,1,n);s=linspace(0,10,n);
[R,S]=meshgrid(r,s); x=[0 1 2 3 4 5];p = binopdf(x,5,0.5);
for k=1:n
f=[S(k,l) S(k,l)*R(k,l) S(k,l)*R(k,l)^2 S(k,l)*R(k,l)^2 S(k,l)*R(k,l) S(k,l)];
for l=1:n
z(k,l)=sum(f.*p);
if z(k,l)>=1 z(k,l)=NaN; end
end
end
contour(R,S,z) 】
3. 单服务台定长服务时间排队系统的计算机模拟
4. 随机变量的模拟:逆概率法
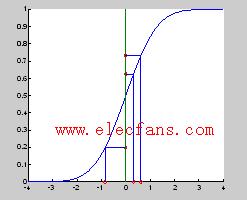
图9.4 逆概率法模拟随机数原理。
【 clf
mu=0;sigma=1;a=mu-4*sigma;b=mu+4*sigma;
t=linspace(a,b,30);
f1=normcdf(t,mu,sigma);
for i=1:3
hold on
u=rand(1);
f=norminv(u,mu,sigma);
plot(t,f1,[0 0],[0,b]),hold on,
plot(0,u,'rO'),plot([0,f],[u,u]);plot([f,f],[u,0]);
plot(f,0,'rO'), axis([-4 4 0 1])
end 】
9.2 实验(Ⅱ) :热轧机的调整
9.2.1实验与观察: 控制粗轧的浪费
1. 用正态分布描述热轧机模型
2. 调整额定长度使浪费最小
.观察程序
zxy9_2.m
【 clf,clear, m=20;l=3;mu=3.5;sigma=0.3; mu1=3.5;sigma1=0.9;
a=0; b=max([mu+4*sigma,mu1+4*sigma1]); %设定坐标的范围。
subplot(2,2,1),
for k=1:m
rand('seed',1), x=normrnd(mu,sigma);
plot([0,x],[k,k],'linewidth',5),hold on, axis([0 mu+4*0.6 -2 m+5])
end
plot([l,l],[-2,m+5],'r-');hold on,axis([a b -2 m+5])
subplot(2,2,3),
t=linspace(a,b,50);f=normpdf(t,mu,sigma);
y0=max(f)+0.1;plot(t,f),hold on,axis([a b 0 y0]),
plot([l,l],[0,y0],'r-',[mu,mu],[0,y0],'r:');hold on
t=linspace(a,b,30);f=normpdf(t,mu,sigma);plot(t,f)
subplot(2,2,2)
for k=1:m
rand('seed',1),x=normrnd(mu1,sigma1);
plot([0,x],[k,k],'linewidth',5),hold on,axis([a b -2 m+5])
end
plot([l,l],[-2,m+5],'r-');hold on
subplot(2,2,4),
t=linspace(a,b,50);f=normpdf(t,mu1,sigma1);y0=max(f)+0.1;
plot(t,f),hold on,axis([a b 0 y0])
plot([l,l],[0,y0],'r-',[mu1,mu1],[0,y0],'r:');hold on 】
下面是观察与实验程序zxy9_3.m,对照上一节给出的算法,这一程序也是不难理解的。
zxy9_3.m
【 clf,clear
l=2;sigma=0.2;
n=10000;m=50;a=2.2;b=3;
mu=linspace(a,b,m);
for k=1:m
x=normrnd(mu(k),sigma,1,n); %模拟轧钢。
k_chenpin=find(x>=l); %求可轧制的成品材的下标。
k_feipin=find(x<l); %求整根报废钢材的下标。
w_chenpin=x(k_chenpin)-l; %计算浪费量。
w_feipin=x(k_feipin); %计算浪费量。
if length(k_chenpin)==0
waste(k)=NaN;
else
waste(k)=(sum(w_chenpin)+sum(w_feipin))/length(k_chenpin);
end
end
[wmin,i]=min(waste); %求最小浪费量及其下标。
[mu(i) wmin]
plot(mu,waste,'.-',mu(i),wmin,'ro'),set(gca,'fontsize',15)
text(mu(i),wmin,['\bullet\leftarrow The Min Value is ',num2str(wmin),' at \it{mu}= ',num2str(mu(i))]); 】
9.2.2应用、思考与练习
1. 随机优化:确定热轧机的额定长度
2. 二维正态分布: 如何制定胖和瘦的标准?
题的思路,这种思路在实践中经常被采用,真正要确定正常体重标准可能要复杂得多。
◆。
【 clear,clf
n=1000;x=normrnd(170,4.5,1,n);
y=0.36*x+normrnd(0,7,1,n);
a=min(x);b=max(x);c=min(y);d=max(y);xx=linspace(a,b,20);
yy=0.36*xx;plot(x,y,'ko'),hold on,
plot(xx,yy,'k-','linewidth',5),grid,
axis([a b c d]),axis('equal'),
xlabel('身高X');ylabel('体重Y'); 】
◆ (2)观察
程序zxy9_4.m (画图9.8)
【 clear,clf,n=1000;m=15;x=normrnd(170,4.5,1,n);
y=0.36*x+normrnd(0,7,1,n);a=min(x);b=max(x);c=min(y);d=max(y);
h1=(b-a)/m;h2=(d-c)/m;
xx=linspace(a-h1,b+h1,m);yy=linspace(c-h2,d+h2,m);
[X,Y]=meshgrid(xx,yy);
for k=1:m %计算频数。
for l=1:m
j=find(x>=(X(k,l)-h1)&x<=(X(k,l)+h1));
h=find(y(j)>=(Y(k,l)-h2)&y(j)<=(Y(k,l)+h2));
z(k,l)=length(h)/n;
end
end
mu=[170 0.36*170]; %计算二维正态分布密度。
C=[4.5^2 0.36*4.5^2; 0.36*4.5^2, (0.36*4.5)^2+7^2];
detC=det(C);
for k=1:m
for l=1:m
u=[X(k,l),Y(k,l)]'-mu';s=2*pi*sqrt(detC);
z1(k,l)=s^-1*exp((-0.5)*u'*C^-1*u);
end
end
subplot(2,2,1),surf(X,Y,z),axis([a b c d 0 0.15]),
set(gca,'fontsize',15);
subplot(2,2,2),contour(X,Y,z),axis([a b c d ]),axis('equal'),
subplot(2,2,3),surf(X,Y,z1),axis([a b c d 0 0.005]),
subplot(2,2,4),contour(X,Y,z1),axis([a b c d ]),axis('equal')】
3.用线性回归方法确定正常体重标准
观察:
◆(1)参考程序 zxy9_4.m中的模拟部分,。
【 alpha=0.01; polytool(x',y',1,alpha) 】
◆(3) 用 多元线性回归指令regress做体重预测。
◆对模拟的100对身高体重数据,运行下面的程序,了解指令regress 的用法。
【 [b,bint,r,rint,stats] = regress(y',[ones(100,1) x']);
b,bint,stats
rcoplot(r,rint),set(gca,'fontsize',15) 】
9.3实验(Ⅲ)参数估计和假设检验
9.3.1实验与观察: 极大似然估计
1.极大似然估计原理: 如何决定废品率?
观察
◆(1)
【 clear,p=0.04; n=10; %设定产品的档次,抽样次数。
for k=1:n %抽样n次。
r(k)=rand(1,1); %产生随机数。
if r(k)<=p
x(k)=1; %抽样得到废品。
elseif r(k)>p
x(k)=0; %抽样得到正品 。
end
end
I=[1:n];[I;x] 】
◆ (2)
2.实验观察的参考程序
实验观察的主要程序为zxy9_5.m,其源代码如下,该程序是不难读懂的。
zxy9_5.m
【 clear,clf,n=50;
p=0.04;
rand('seed',1),r=rand(1,n);
k=+find(r<=p);
x=zeros(1,n);
x(k)=ones(1,length(k));
p_estimate=sum(x)/n,
t=[0.01 0.02 0.03 0.04 0.05 0.06];
%t=linspace(0.01,0.5,40)
Lt=t.^sum(x).*(1-t).^(n-sum(x));
%lnLt=sum(x)*log(t)+(n-sum(x))*log(1-t);
set(gca,'fontsize',16),
plot(t,Lt,''),
[Lmax,I]=max(Lt);
tmax=t(I);
text(t(I),Lmax,['\fontsize{16}\leftarrow\it Lmax=' ,num2str(Lmax)])
text(t(I),0.95*Lmax,['\fontsize{16}\it{ at p}= ',num2str(tmax)])
xlabel('p','fontsize',16);ylabel('L(p)','fontsize',16); 】
9.3.2 应用、思考与练习
1. 用Matlab符号演算求解极大似然估计
◆ 练习:用Matlab符号演算指令求解9.3.1节中废品问题的似然方程获得极大似然估计。
【 syms p %未知参数为p,所以作为符号变量处理,用syms指令说明。
clear,clf,n=50; %产生50个样本。
p=0.04; %设定真实参数。
x=zeros(1,n); %令x全为0 。
rand('seed',1),r=rand(1,n);
k=+find(r<=p); %找出废品的下标。
x(k)=ones(1,length(k)); %在废品下标处改x为1;x为50个样本观察值。
%观察似然函数和似然方程的一般表达式。
L=sym('p^sx*(1-p)^(n-sx)') %正确写出似然函数,L是符号p的函数。
likely_equ=diff(L,'p') %对p进行符号求导,得到似然方程。
%观察含具体数值的似然函数和似然方程
sx=sum(x), p='p'; %代入sx的具体数值。
Lp=subs(L) %将具体的数值代入似然函数中 。
likely_equ=diff(Lp,'p') %求似然方程 。 】
【 %求似然方程的符号解,得到极大似然估计
s=solve('p^sx*sx/p*(1-p)^(n-sx)-p^sx*(1-p)^(n-sx)*(n-sx)/(1-p)=0','p')
sx,n %看看具体的数值。
sp=subs(s) %对已获得的样本,观察极大似然估计的具体数值。 】
2. 水库入库径流的分布估计
7月上旬径流数据
356 258 222 208 163 342 501 501 782 225 630 2305
931 485 503 501 422 101 280 1807 922 390 466 211
922 444 233 370 788 802 219 524 470 1097 1160 702
566 222 630
7月中旬径流数据
98 262 117 1687 291 1318 292 716 254 519 270 273
275 274 374 147 345 70 940 440 2839 141 699 324
900 311 870 596 187 2231 111 949 303 888 328 459
370 1360 1320
7月下旬径流数据
69 133 392 596 4518 1051 336 867 541 1733 149 266
324 1365 891 918 1751 219 513 438 1033 1217 1290 247 2360 1023 453 1622 1272 1383 1217 1530 1724 703 299 638
548 1200 1220
zxy9_6.m
【 clear,clf,
Q=[ 98 262 117 1687 291 1318 292 716 254 519 270 273 275 274 374 147 345 70 940 440 2839 141 699 324 900 311 870 596 187 2231 111 949 303 888 328 459 370 1360 1320];
m=50;
as=linspace(0.6561, 2.2477,m);
bs=linspace(215.4687, 637.4421,m);
[A B]=meshgrid(as,bs);
for i=1:m
for j=1:m
ax=A(i,j);bx=B(i,j);
y(i,j) = sum(log(gampdf(Q,ax,bx)));
end
end
[y0,s]=max(y); [y00,s0]=max(y0);
a_est=A(s0,s(s0));b_est=B(s0,s(s0)); meshc(A,B,y),hold on
plot3(a_est,b_est,y00,'.','markersize',25);
text(a_est,b_est,y00+0.06*abs(y00),['(a_e_s_t,b_e_s_t,L_m_a_x)=']);
text(a_est,b_est,y00+0.03*abs(y00),['(',num2str(a_est),',',num2str(b_est),',',num2str(y00),')'])
figure(2)
[h,n0]=hist(Q,5); h0=max(h); a=min(Q)-100;b=max(Q);
x=linspace(a,b,30); hist(Q,5); hold on
y = gampdf(x,a_est,b_est);
plot(x,h0*y/max(y),'r-','linewidth',5); 】
3. 数学建模竞赛: 零件的参数设计
zxy9_7.m
【 clear,clf, n=1000; A=0.01/3;B=0.05/3;C=0.1/3;
%x=[0.075,0.375,0.125,0.1198,1.252,12.5,0.77];%A=[B B B C C B B];
x=[0.1 0.3 0.1 0.1 1.5 16 0.75]; %设置标定值。
A=[B C C C C C B]; %设置容差。
X1=normrnd(x(1),A(1)*x(1),n,1); %模拟零件参数。
X2=normrnd(x(2),A(2)*x(2),n,1);X3=normrnd(x(3),A(3)*x(3),n,1);
X4=normrnd(x(4),A(4)*x(4),n,1);X5=normrnd(x(5),A(5)*x(5),n,1);
X6=normrnd(x(6),A(6)*x(6),n,1);X7=normrnd(x(7),A(7)*x(7),n,1);
Y=z9_5fun(X1,X2,X3,X4,X5,X6,X7); %模拟y的样本。
k=find(imag(Y)==0);Y1=Y(k); %如果产生了复数,剔除复数。
histfit(Y1) %直方图和正态密度拟合。
dh=0.001; %求数值导数。
for i=1:7
for j=1:7
xx(:,j)=x(j)*ones(2,1);
end
xx(:,i)=linspace(x(i),x(i)+dh,2)';
F(:,i)=z9_5fun(xx(:,1),xx(:,2),xx(:,3),xx(:,4),xx(:,5),xx(:,6),xx(:,7));
g(:,i)=diff(F(:,i),1)/dh; %求数值导数。
end
mu=F(1,1),EY=mean(Y1), %均值对比。
R=(A.*x).^2;
sigma=sqrt(sum((g.^2).*R)),DY=std(Y1), %均方差值对比.
[h,p,ci]=ttest(Y1,mu,0.01,0) %均值的t-检验 。 】
zxy9_6fun.m(计算函数的子程序)
【 function y=zxy9_5fun(x1,x2,x3,x4,x5,x6,x7)
y1=174.42*(x1./x5).*(x3./(x2-x1)).^0.85;
y2=(1-0.36*(x4./x2).^(-0.56)).^(1.5) ;
y3=(1-2.62*y2.*(x4./x2).^1.16)./(x6.*x7);
y=y1.*sqrt(y3);
 电子发烧友App
电子发烧友App




















评论