一、引言
中频PCM/DPSK遥测信号全软化解调器就是采用软件的方法对直接中频采样的数字信号进行解调。中频采样的结果使得数据量大大增加,从而给后续的数字信号处理带来了压力。为了解决这个问题,在全软化解调器中,对下变频到基带后的高采样率信号进行抽取滤波,在满足奈奎斯特定律的前提下尽量减少基带信号数据量,之后再对抽取后的基带信号进行运算处理工作。本文将针对中频PCM/DPSK遥测信号全软化解调器中数字级联抽取滤波器的设计及软化实现进行研究。?
二、基本原理
由于窄带数字中频处理中输入信号的抽样率很高而且要求抽取滤波器的通带带宽和传输带很窄,这将使滤波器的节数很大,运算效率很低。因此,为了有效地实现抽样率转换,本文将采用多级抽取的方法。由于将滤波器分解成了多级,采用不同形式的数字滤波器进行抽取,使每一级滤波器的相对过渡带大大增加,相应每一级滤波器的节数大为减少,因而可大大减少滤波的运算量与滤波器系数的存储量。
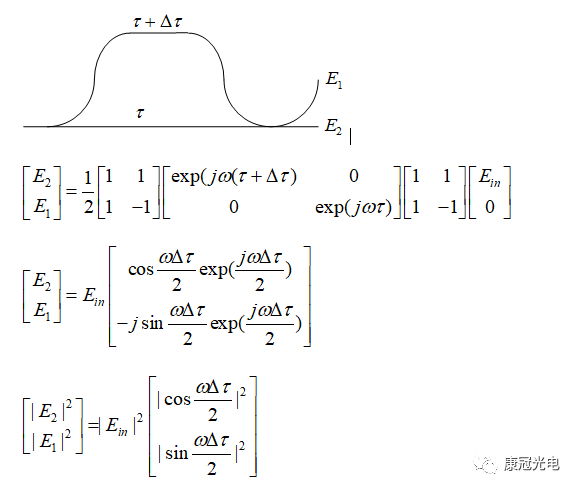
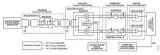
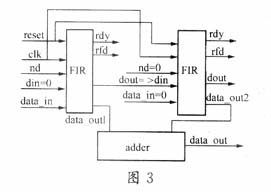
中频PCM/DPSK遥测信号全软化解调器中数字级联抽取滤波器根据抽取比为10的要求分成3级:梳状抽取滤波器实现5倍信号抽取,半带抽取滤波器实现2倍信号抽取以及一般低通滤波器完成补偿滤波。其组成结构框图如图1所示。其中H1(z)、H2(z)和H3(z)分别表示的是梳状滤波器、半带滤波器和一般低通滤波器的频响,fs为输入抽样率,f1=fs/5为经过梳状抽取滤波器后的输出采样率,f2=fs/10。
???
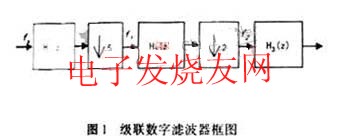
三、滤波器设计
抽取滤波器是由滤波器和抽取器组成,所以无论是何种形式的抽取滤波器实际上都是数字低通滤波器,因此本文采用等波纹法设计各级FIR抽取滤波器,并利用Matlab完成了该级联抽取滤波器的设计。 1.梳状抽取滤波器(CIC)
由于采样后的数字信号频谱是原interwetten与威廉的赔率体系 信号频谱按照采样率为周期进行延拓,为了保证信号在抽取的过程中不会造成基带频谱混叠,所以要对有可能混进基带频谱的部分进行滤除。鉴于这种考虑,在多级滤波器的第一级采用梳状滤波器,而对位于基带和阻带之间的过渡带则通过后面的滤波器进行滤除。
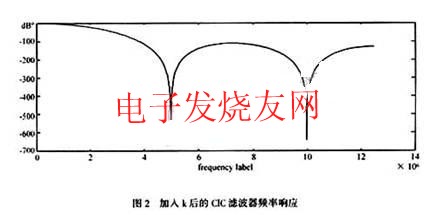
CIC滤波器是一种线性相位低通FIR滤波器,其系数均为1,实现起来较为简便,但研究表明,这样得出的滤波器的阻带衰减较小,不能满足实际需要。为了提高滤波器的阻带衰减,采用CIC滤波器的修正形式:?
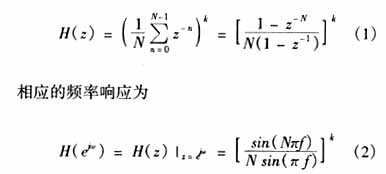
图2所示的是N=5,k=4时的梳状滤波器的频率响应图。从图中可以看到,频率响应得到了明显的改善,其阻带衰减达到80 dB,滤波器的长度为p=17。此时,梳状滤波器频响H1(z)为?
2.半带抽取滤波器
半带滤波器是一种特殊的线性相位滤波器,它将近有一半的系数精确为零,因此其实现滤波的运算量与同样长度的其它线性相位滤波器相比减少将近一半。根据半带滤波器的频率特性和运算量少的优点,可用它来作为变换因子为2的抽取或插值滤波器。
但若直接采用等波纹滤波器的设计方法来设计半带滤波器,滤波器的将近一半系数为零的条件无法加以利用,滤波器的设计过程将需要较长的时间。所以,先用等波纹法设计一个满带线性相位滤波器原型,再在这个原型的基础上进行半带滤波器的设计[3]。设计中,通带边频ωp=(2e+6)Hz,阻带边频ωc=(2.5e+6)Hz,通带波纹δp=1 dB,得到g(n)的阶数为m=19。然后再根据m=(N-1)/2的关系求出半带滤波器的阶数N=39,最后得到半带滤波器的系数h2为
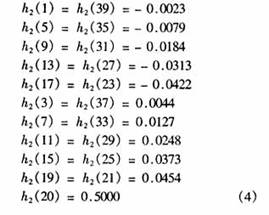
其余偶数位置系数均为零。
用上述方法设计半带滤波器,仅利用了设计长为 (N-1)/2=(39-1)/2=19的滤波器的代价设计出了长为N=39的半带滤波器,因此对于大的N值,这就大大节约了设计时间并可获得较高的设计精度。半带滤波器的频率响应如图3所示。
3.一般低通滤波器
虽然CIC滤波器具有低通特性,但通带内并不平坦,而是有一定的滚降,从而使信号频谱产生失真。信号的带宽越宽,则产生的失真越严重。因此,需要用普通FIR滤波器进行补偿。CIC滤波器的频率响应为H1(z),则补偿滤波器在通带内的频率响应为

四、结束语
本文采用级联抽取滤波的原理和方法实现了中频PCM/DPSK遥测信号解调中的数字抽取滤波器的设计,可用于高采样率情况下数字信号的抽取滤波,使采样时刻由基带提前到了中频,减少了前端的硬件电路,降低了系统的复杂度,提高了系统的精度。
 电子发烧友App
电子发烧友App





















评论