混合叠压电机的齿槽转矩分析

正文部分

电机铁心是电机内的关键部件，其性能的改善对电机整体性能的提升具有重要意义。永磁电机本身性能较为优异，同时与一般的电机设计相比，再制造电机还受到原有铁心结构的限制，因此其性能难以提升。传统电机铁心材料一般选用冷轧硅钢片，而非晶合金材料与硅钢片相比，其加工过程更加环保，且具有更低的铁心损耗，应用于电机铁心可以使电机铁耗显著降低，从而提高效率。

1 电机参数及混合叠压方法

1.1 定子材料

原电机所用的硅钢材料牌号为B35AV1900，所用非晶合金材料牌号为Metglas2605SA1。图1为由湖南联众MATS-2010S软磁测量装置测得的硅钢材料和非晶合金试样的磁化曲线。对比两者磁化曲线可知，硅钢材料的饱和磁通密度（简称“磁密”）约为1.80 T，非晶合金的饱和磁通密度约为1.44 T，在相同磁场强度情况下，非晶合金对应的磁通密度小于硅钢材料的磁通密度。

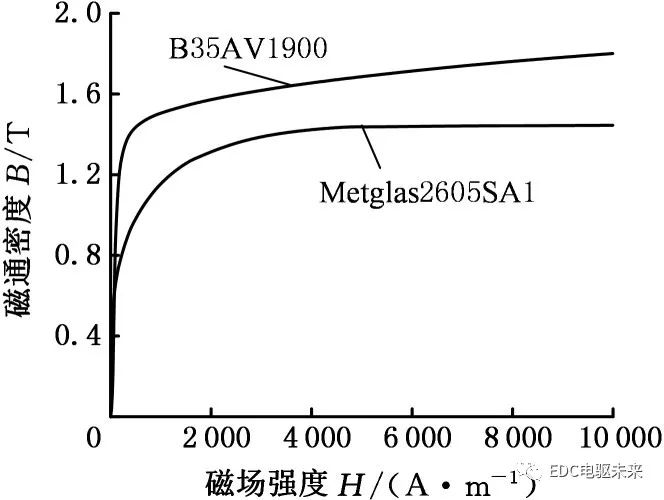
图1 硅钢和非晶合金的磁化曲线
Fig.1 Magnetization curves of silicon steel and amorphous alloy

1.2 电机参数

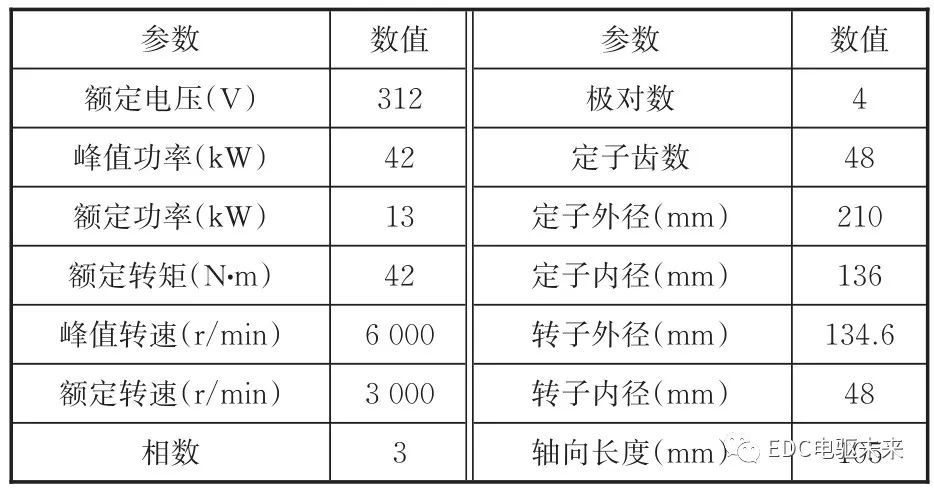
以一台8极48槽内置式永磁同步电机为例进行定子混合叠压再制造。电机的参数见表1。

表1 电机主要参数
Tab.1 Main parameters of motor

1.3 混合叠压方法

受到原铁心材料和结构的限制，再制造的电机铁心性能较差。利用性能优异的非晶材料替换原铁心，可以显著降低铁心的损耗，但非晶材料饱和磁密较小，且成本较高。通过合理选择材料比例，将非晶材料与硅钢材料组合使用，既能降低电机损耗、提升电机综合性能，又能充分利用零部件，降低再制造成本。定子混合叠压是将不同材料沿电机轴向间隔叠压制成定子铁心，规定相同材料的每段叠片段长度相等。再制造时，不同叠片段除材料不同外，铁心结构与尺寸均相同，并保持与原电机一致。混合叠压定子见图2，其中A和B代表不同的材料。

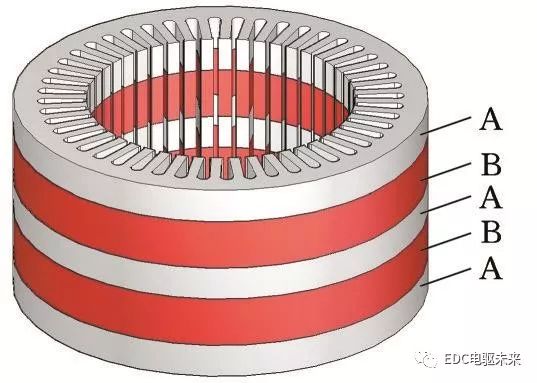
图2 混合叠压定子铁心
Fig.2 Hybrid laminated stator core

2 混合叠压电机的齿槽转矩分析

由文献［13］可知，对于使用同种材料的永磁同步电机，根据能量法，齿槽转矩可以定义为空载时电机内部磁场能量与定转子相对位置角的负导数，即

式中，Tcog为齿槽转矩；W为磁场能量；α为定转子相对位置角。

在混合叠压电机中，定子由不同的材料组合而成，材料本身的磁导率不同，对电机内部与气隙中磁场的分布具有一定影响；同时非晶材料饱和磁密较小，对材料交界面区域处的磁场分布具有一定的影响，但通常而言，其影响范围与程度不会很大。考虑到定子混合叠压电机的特征，若不计材料间的相互影响，可通过各材料段对应区域能量的叠加得到电机内部的总能量，进一步便可得到定子混合叠压电机的齿槽转矩：

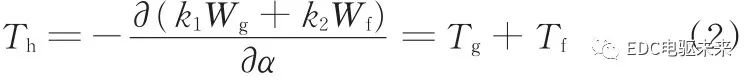
式中，Th为混合电机的齿槽转矩；Wg为硅钢段区域对应的磁场能量；Wf为非晶段区域对应的磁场能量；k1、k2分别为硅钢和非晶的分段数；Tg为硅钢叠片段的齿槽转矩之和；Tf为非晶叠片段的齿槽转矩之和。

由式（2）可知，在忽略材料间相互影响的情况下，混合叠压电机的齿槽转矩可以由对应材料各自齿槽转矩的叠加得到。若引入材料混合比，并以电机轴向长度为基准，则混合电机齿槽转矩近似计算为

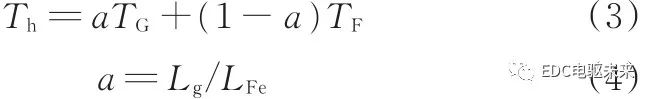
式中，TG、TF分别为纯硅钢定子电机和纯非晶定子电机的齿槽转矩；a为硅钢材料所占的比例；Lg为硅钢材料所有叠片分段的轴向长度之和；LFe为定子轴向长度。

由式（2）和式（3）可知，利用对应材料的二维有限元计算结果近似叠加可得到混合电机的齿槽转矩，可避免复杂的解析推导和三维分析，这为混合电机齿槽转矩的优化设计和研究提供了便利。

3 再制造电机齿槽转矩分析

3.1 混合叠压电机模型的建立

考虑到三维仿真时间长，占用资源多，本文利用Ansoft内部计算软件Rmxprt生成原电机1/8模型。在此基础上将定子铁心删除，替换为混合叠压定子铁心，即得到定子混合叠压再制造电机的仿真模型。

齿槽转矩的仿真对网格要求较高，因此将绕组删除，减少网格数量，采用气隙分层的方法加密网格，同时电机转速设置成低转速，以保证分析结果的准确性。剖分结果见图3。

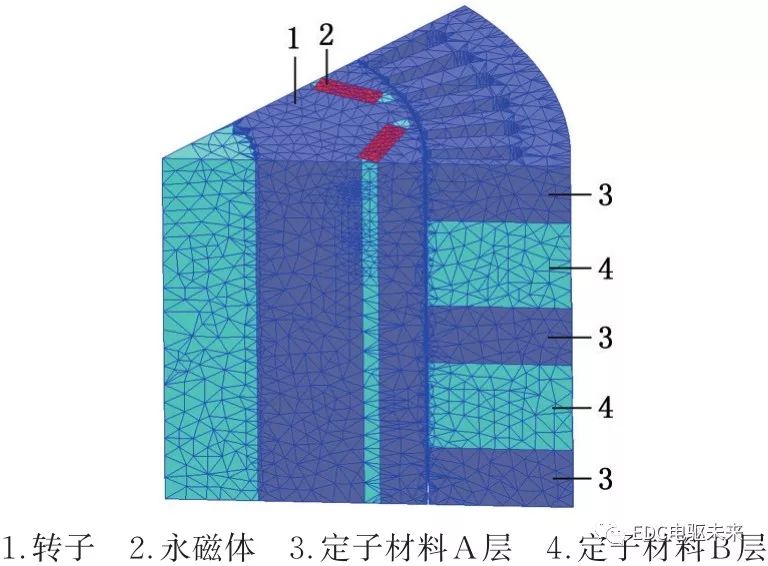
图3 电机网格剖分
Fig.3 Mesh generation of motor

3.2 材料对齿槽转矩的影响

定子混合叠压再制造电机的定子由两种材料混合叠压制成。两种材料的磁性能不同，在研究不同材料的混合比例和叠压方式对齿槽转矩的影响规律之前，有必要对不同材料本身对电机齿槽转矩的影响规律进行研究。再制造电机所用材料为非晶材料和硅钢材料，对图3所示模型中定子的所有分层同时赋予硅钢或非晶材料，得到两种材料的齿槽转矩波形图，见图4。

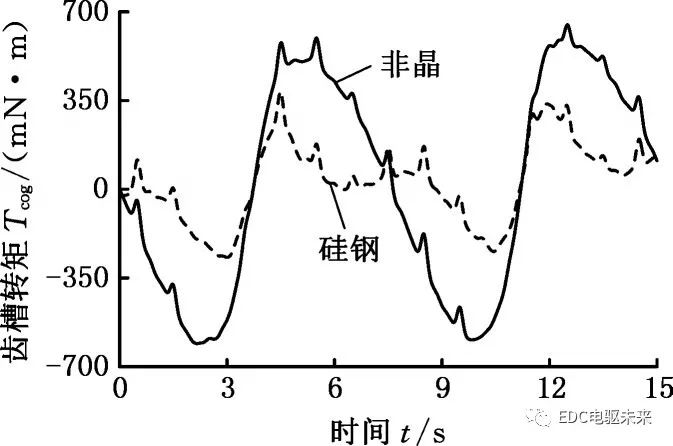
图4 不同材料的齿槽转矩
Fig.4 Cogging torque of different materials

由图4可以看出，两种材料齿槽转矩波形不同，幅值相差较大。对其波形进行傅里叶分解，得到谐波幅值图，见图5。

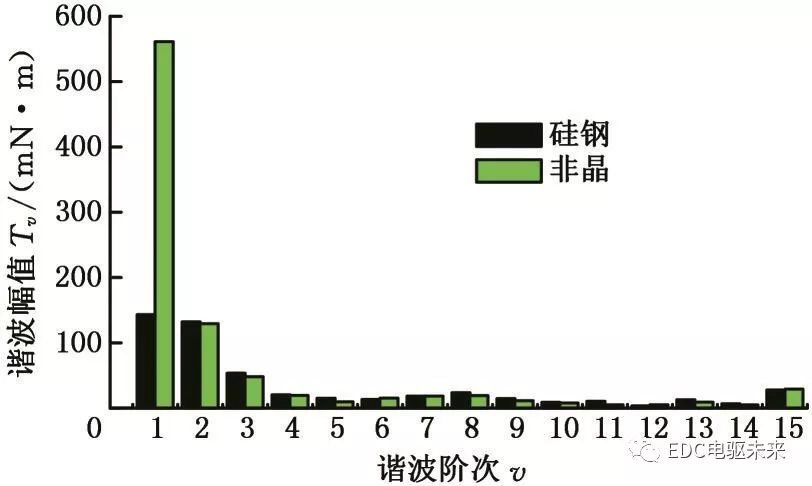
图5 不同材料齿槽转矩的谐波分析
Fig.5 Harmonic analysis of the cogging torque of different materials

对比各次谐波的大小可知，非晶电机基波幅值为561 mN·m，硅钢电机基波幅值为143 mN·m，非晶电机基波幅值大约是硅钢电机的4倍；其他各次谐波幅值大小基本相同，最大差值为10 mN·m。结果表明，对替换定子而言，硅钢与非晶两种材料磁性能的差异对齿槽转矩的影响主要体现在基波幅值上，对其他各次谐波的影响较小。对于定子由这两种材料混合叠压而成的电机，两种材料混合使用引入的相互间的影响情况以及不同叠压方式带来的附加影响情况还有待研究。

3.3 叠压方式对齿槽转矩的影响

以50%比例混合为例（硅钢与非晶材料以1∶1的比例混合叠压制成再制造电机定子铁心）研究不同叠压方式对混合电机齿槽转矩的影响规律。对图3所示定子中3、4对应的分段分别以硅钢-非晶和非晶-硅钢的顺序赋予材料，得到两种混合叠压定子；其叠压顺序不同，对应材料的分段数也不同。用这两种定子替换原电机定子，进行有限元仿真，得到两种叠压方式下电机的齿槽转矩，见图6。

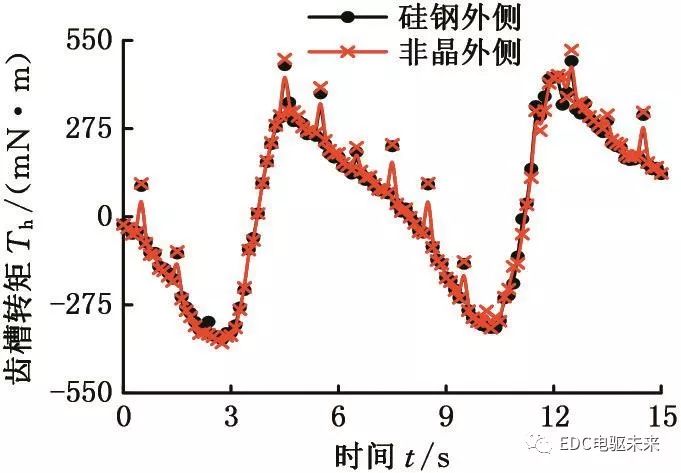
图6 不同叠压方式的齿槽转矩
Fig.6 Cogging torque with different stacking modes

从图6中可以看出，不同叠压方式下电机的齿槽转矩波形基本一致。对这两种叠压方式下电机齿槽转矩波形进行傅里叶分解，得到两者各次谐波幅值，见图7，可以看出，不同叠压方式下，电机的基波与各次谐波幅值相差较小，最大差值为11 mN·m。分析结果表明，随着材料分段数和叠压顺序的变化，电机齿槽转矩没有明显的变化。可以认为在空载的情况下，当混合比例与总的分段数一定时，各材料的分段数和叠压顺序不会改变电机内部磁场能量的变化规律，因此对齿槽转矩的影响较小。

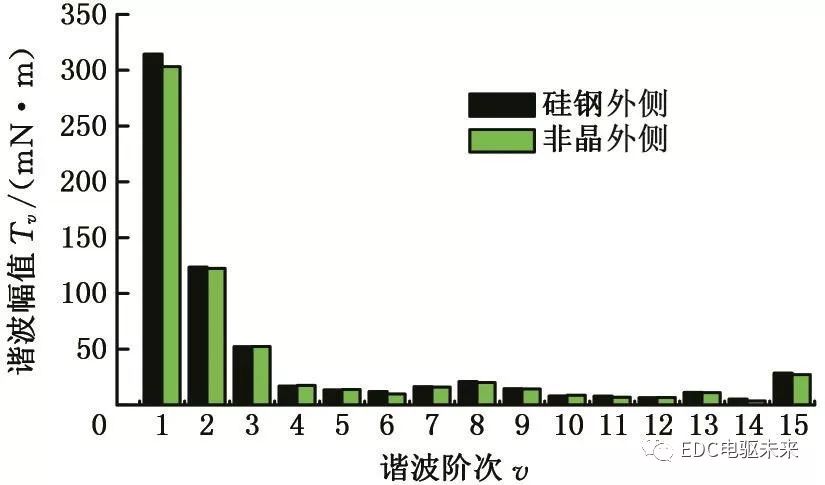
图7 不同叠压方式的齿槽转矩谐波分析
Fig.7 Harmonic analysis of cogging torque with different stacking modes

3.4 齿槽转矩的分段叠加

由于电机铁心内部磁场分布较为复杂，混合电机的磁场分布规律尚不明确，故解析计算较为困难。现以硅钢与非晶材料以1∶1、1∶5、5∶1比例进行混合叠压为例进行研究。通过二维仿真得到定子由纯硅钢材料和纯非晶材料组成的电机的齿槽转矩，并根据式（3）按照相应的材料混合比例进行叠加近似计算。叠加结果与三维整体仿真所得齿槽转矩进行对比。结果如图8～图10所示。

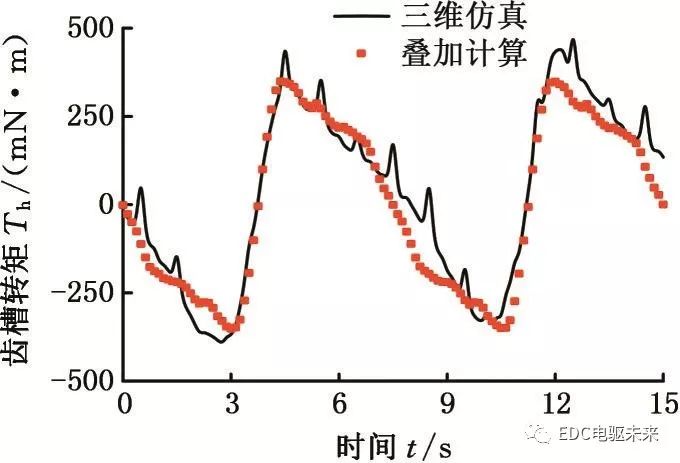
图8 硅钢非晶1∶1混合时的齿槽转矩
Fig.8 Cogging torque of silicon steel and amorphous material when mixed with 1∶1 ratio

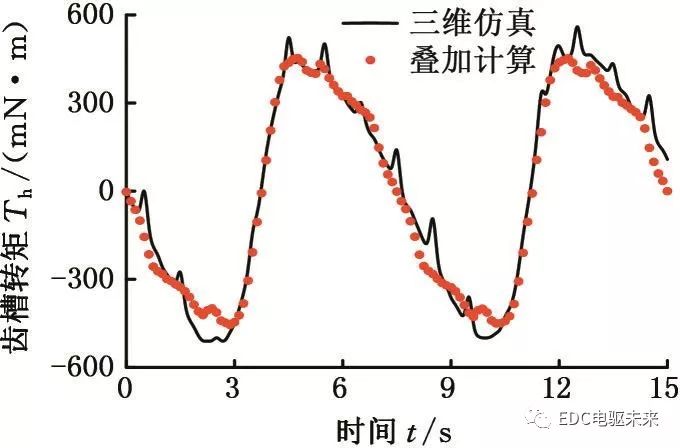
图9 硅钢非晶1∶5混合时的齿槽转矩
Fig.9 Cogging torque of silicon steel and amorphous material when mixed with 1∶5 ratio

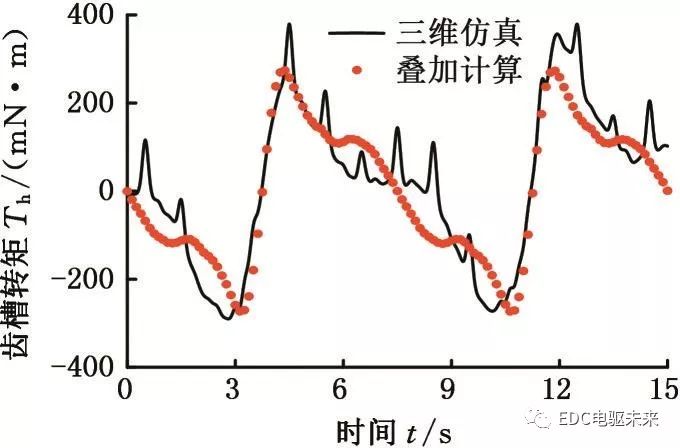
图10 硅钢非晶5∶1混合时的齿槽转矩
Fig.10 Cogging torque of silicon steel and amorphous material when mixed with 5∶1 ratio

分别对比两者齿槽转矩波形可知：由于二维计算无法考虑端部效应以及材料之间的相互影响，故叠加所得齿槽转矩与三维仿真结果存在一定的差异；不同比例下叠加计算所得齿槽转矩幅值与三维仿真所得齿槽转矩幅值相差不大，且波形基本一致。对比分析验证了分段叠加近似计算混合叠压电机齿槽转矩的有效性，节约了时间和资源，为齿槽转矩的优化分析提供便利。

4 混合比例的选取与齿槽转矩的优化

由非晶合金与硅钢材料的磁化曲线可知：一方面，同一外磁场作用下，非晶合金的磁密较小，应用于定子铁心，能显著降低电机的铁心损耗，但非晶材料的饱和磁密较小，在同样磁场激励下，非晶材料更容易饱和，导致其磁导率下降，对气隙磁密和电机各项性能造成一定影响；另一方面，通过不同比例下齿槽转矩的对比可知，混合叠压之后得到的电机齿槽转矩大于原硅钢电机的齿槽转矩，且会随着非晶材料比例的增大而增大；此外，由于非晶合金本身脆硬的特性，其加工较为困难，成本也相对较高。结合文献［8］给出的再制造成本特征，混合叠压时，应综合考虑再制造成本与电机性能，选取合适的材料比例。

4.1 不同比例下电机性能分析

不同比例下混合叠压电机与原硅钢电机各项性能参数见表2。

对比不同混合比例下电机与原电机的各项参数可知：空载时混合叠压电机与原硅钢电机相比，磁链与电动势基本不变，电动势的谐波畸变率变小，气隙磁密幅值略有降低，且非晶段的气隙磁密幅值明显低于硅钢段的气隙磁密幅值，同时随着非晶材料比例的增多，齿槽转矩逐渐增大；额定工况下，由于非晶材料优越的低损耗特性，电机损耗明显下降，电机效率略有提升，但由于非晶材料的饱和磁密较小，因此输出转矩略有收缩，且收缩率随着非晶材料比例的增大而增大。

由对比分析结果可知，混合叠压电机相比于原电机，空载性能基本不变，电机损耗明显降低，但也存在齿槽转矩增大，输出转矩减小的问题。为综合考虑混合叠压电机损耗降低与转矩收缩的影响，选择合适的材料比例，现以定子材料为纯非晶合金作为基准，将不同混合比例下电机效率的提升值进行换算，换算公式为

表2 电机性能参数对比
Tab.2 Comparison of motor performance parameter

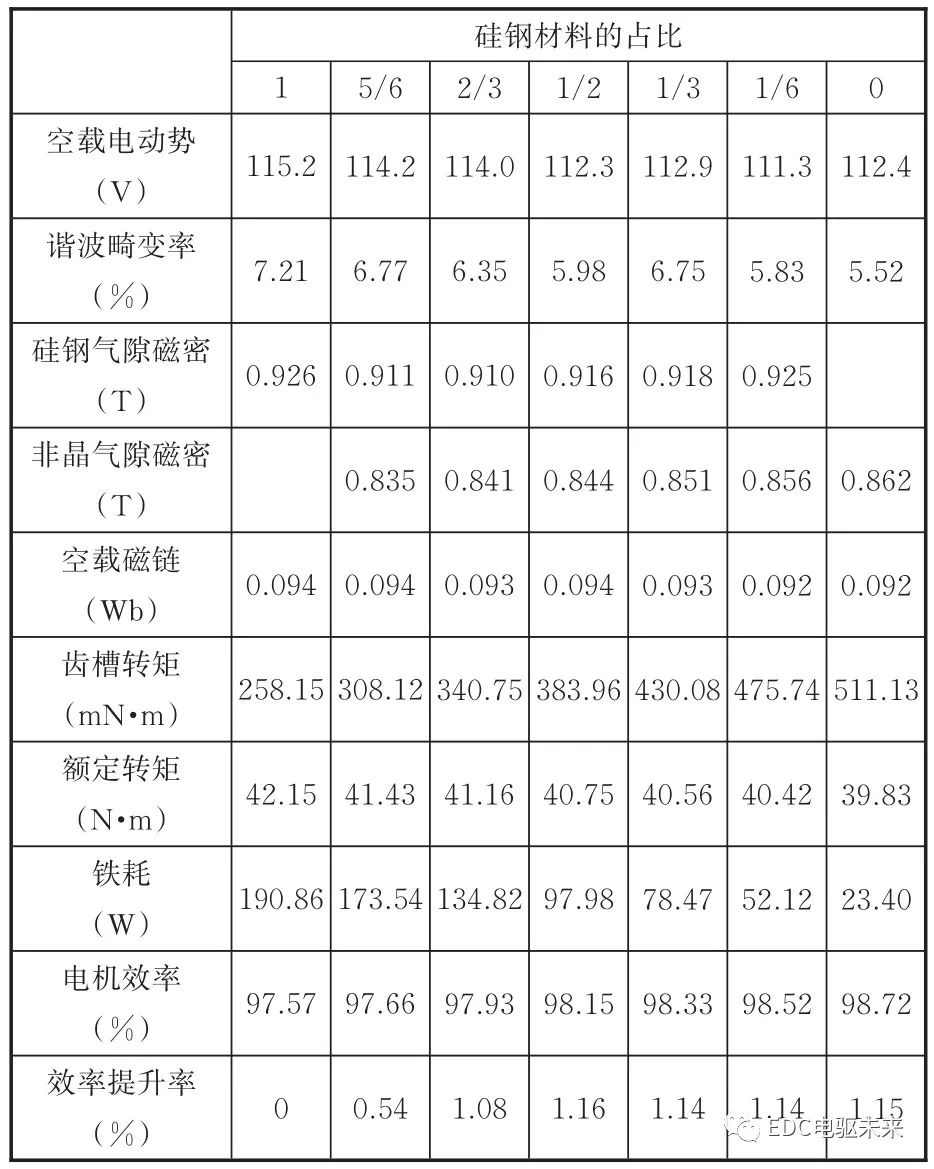
注：除输出转矩与铁耗为平均值外，其余参数均为幅值。其中气隙磁密为空载时电机气隙中间位置处的磁密幅值；转矩与铁耗为额定工况下仿真所得的数据。

式中，Δη为电机的效率提升率；ηi为不同混合比例时电机的效率；ηn为纯硅钢电机的效率。

由计算结果得到不同比例下非晶合金对电机效率的提升率，见图11。由图11可见，随着非晶合金比例的增大，电机效率的提升率增大，在非晶占比高于50%后，提升率趋于稳定。从再制造成本考虑，对于本款电机，非晶合金与硅钢材料以1∶1比例混合较为合适。

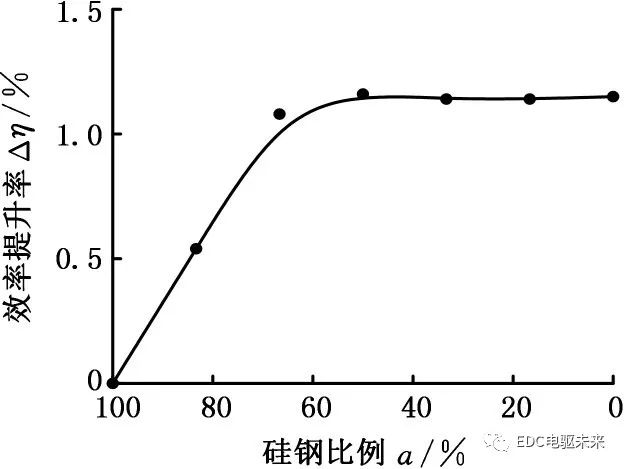
图11 电机效率提升率
Fig.11 Efficiency improvement rate of motor

4.2 齿槽转矩的分段斜槽优化

传统的斜槽工艺中，通过将定子在整个轴向长度上倾斜不同的角度，以减少对应的齿谐波，达到减小齿槽转矩的目的，但定子的倾斜角度不宜过大。基于分段叠加近似计算方法，本文提出了分段设置反向斜槽的方法，即对每段叠片段进行斜槽处理，通过减小每段叠片段的齿槽转矩来减小整体的齿槽转矩。分段反向斜槽示意图见图12。图中竖直方向为电机轴向；粗实线表示沿轴向槽的倾斜方向与倾斜程度的变化；Ns表示每段的斜槽数。

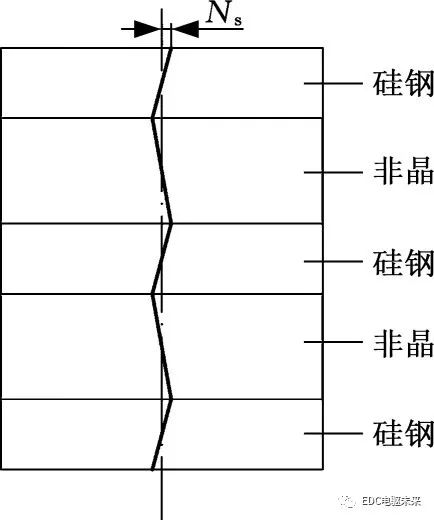
图12 分段斜槽示意图
Fig.12 Segmented reverse skewed slots diagram

通过多层分段二维有限元法，将每一段叠片段分为5层，每一层近似为直槽电机，通过设置不同的转子初始角度interwetten与威廉的赔率体系 三维斜槽结构，并将仿真结果叠加，得到1∶1混合比例下正向斜槽与反向斜槽后电机的齿槽转矩，见图13。可以看出，正向斜槽时，当每段斜槽数为0.25与0.75时，齿槽转矩的幅值较小，分别为25.05 mN·m与10.68 mN·m。这是因为，正向斜槽时，相同材料段间隔布置，其初始角度不同，对于8极48槽电机而言，齿槽转矩的周期为一个槽距，当斜槽数为0.25的奇数倍时，相同材料段，尤其是非晶材料段的齿槽转矩波形相差半个周期，出现了正负抵消的情况。反向斜槽时，随着每段叠片段斜槽数的增大，齿槽转矩幅值逐渐减小，当斜槽数为0.75时，齿槽转矩幅值达到最小，为29.12 mN∙m。

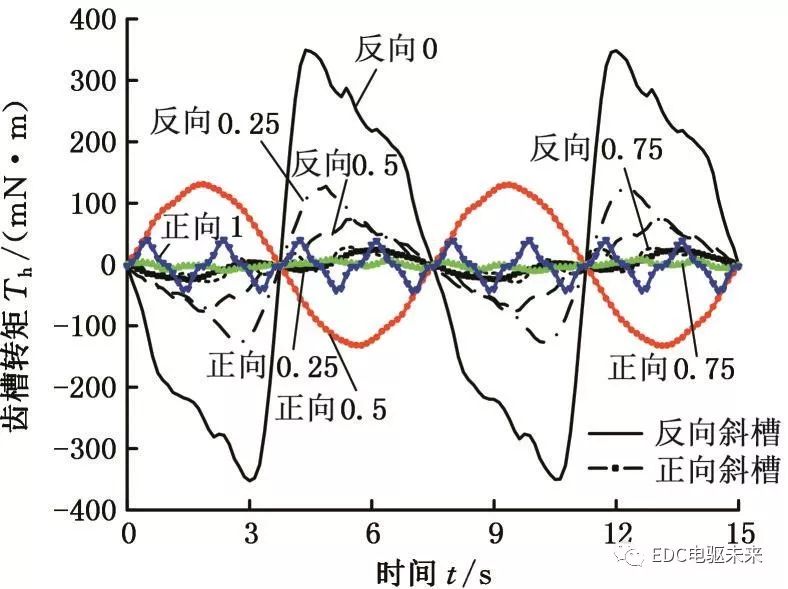
图13 混合叠压电机斜槽后的齿槽转矩
Fig.13 The cogging torque after skewed of the hybrid electric motor

由图13的分析可知，正向斜槽与反向斜槽都能有效减小电机的齿槽转矩，在不考虑定子轴向总的倾斜角度时，正向斜槽的效果较好。定子斜槽时，尤其是正向斜槽时，若轴向总的倾斜角度过大，会对电机的电动势造成较大的影响。选取正向斜槽数为0.25与0.75，反向斜槽数为0.75，通过分段二维有限元法，得到电机的电动势，见图14。其中原电机的空载电动势幅值为115.20 V，谐波畸变率为7.21%。正向斜槽数为0.25和0.75时，电机的空载电动势幅值分别为108.18 V和99.23 V；反向斜槽数为0.75时，电机的空载电动势幅值为110.33 V；通过傅里叶分解计算空载电动势的谐波畸变率，正向斜槽数为0.25、0.75与反向斜槽数为0.75时，电动势谐波畸变率分别为5.30%、1.28%和4.16%。可见相比于原电机，斜槽后空载电动势的谐波畸变率均得到一定优化，但当正向斜槽数为0.75时，空载电动势相比原来明显减小。反向斜槽数为0.75与正向斜槽数为0.25相比，齿槽转矩略小，空载电动势幅值较大，谐波畸变率较小，因此反向斜槽在有效减小电机齿槽转矩的同时，能保证更好的电机性能。

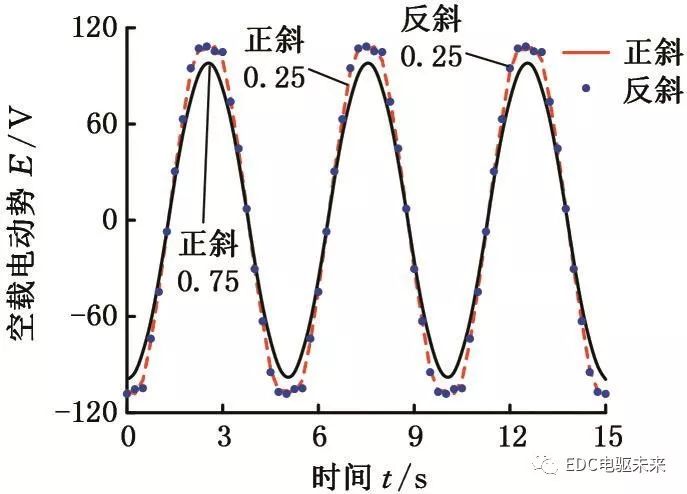
图14 空载电动势对比
Fig.14 Comparison of No-load EMF

5 结论

（1）基于能量法提出用二维分段叠加近似替代三维计算的定子混合叠压电机齿槽转矩计算方法，并通过仿真分析验证了二维叠加近似计算混合叠压电机齿槽转矩的可行性，简化了齿槽转矩的优化分析。

（2）对比分析了不同混合比例下电机的各项性能参数。随着非晶比例的增大，混合叠压再制造电机的空载性能基本不变；额定工况下电机损耗降低、效率提高的同时，齿槽转矩增大，输出转矩减小，电机效率提升率逐渐升高，当占比高于50%时趋于稳定；结合成本考虑，对于本款电机，选取再制造定子材料混合比例为1∶1。

（3）对正反斜槽后电机的齿槽转矩与空载电动势进行对比分析，正向斜槽对齿槽转矩的减小效果更好，反向斜槽对空载电动势幅值的影响较小；在确保空载电动势幅值的情况下，对于本款电机，正向斜槽数为0.25与反向斜槽数为0.75时，电机的齿槽转矩最小。

（4）对定子由纯硅钢和纯非晶组成的电机齿槽转矩进行了对比分析，研究了材料对齿槽转矩的影响。定子采用非晶材料时齿槽转矩的基波幅值大约是采用硅钢材料时齿槽转矩的基波幅值的4倍，其余各次谐波幅值相差不超过10 mN·m。定子材料对齿槽转矩的影响主要体现在基波幅值上。

（5）仿真分析了不同混合叠压方式下电机的齿槽转矩。各次谐波幅值中最大差值约为11 mN·m，在一定的混合比例和总的分段数下，材料的分段数与混合叠压顺序对电机齿槽转矩，即能量的变化规律影响较小。