摘 要: 本文介绍了一种新的复用器重构算法,能够降低FPGA实际设计20%的成本。该算法通过减少复用器所需查找表(LUT)的数量来实现。算法以效率更高的4:1复用器替代2:1复用器树。算法性能的关键在于寻找总线上出现的复用器数量。新的优化方法占用一定的逻辑,这些逻辑由总线进行分担,从而减少了总线上每个比特位所需的逻辑。 (本站编者:该算法已经集成在QuartusII4.2软件中,使用QuartusIi进行综合HDL语言时会自动调用该算法进行综合,本文介绍该算法的详情,本文适合希望深入了解算法的用户阅读)
关键词: FPGA;复用器;重构;重新编码;总线;逻辑优化;综合
1. 引言
--- 复用器是数据通道常用的构建模块,被广泛应用在处理器[1]、处理器总线、网络交换,甚至是资源共享的DSP设计中。据估计,复用器一般要占用一个FPGA设计[2] 25%以上的面积。因此,优化FPGA设计的关键在于怎样优化复用器。
--- 本文介绍了一种新的复用器重构算法,该算法减小了复用器在基于4输入查找表(4-LUT)FPGA体系结构中所占用的面积。基准测试结果表明复用器平均减少了17%,在一些设计中,4-LUT整体减少20%。
--- 2.1节阐述了复用器是如何由行为级VHDL[4]或Verilog[5]代码产生的,2.2和2.3节阐述复用器树和复用器总线在设计中是怎样生成的。2.4节说明这些结构怎样由4-LUT实现,阐述如何采用两个4-LUT有效实现一个4:1二进制复用器。
--- 第3节介绍了一种叫做压缩的新威廉希尔官方网站 ,该威廉希尔官方网站 附加一些控制逻辑,将多个2:1复用器重新组合为有效的4:1复用器,从而减少了为总线上每一个比特位实现复用器所需要的4-LUT数量,所附加的控制逻辑代价由整个总线来分担。优化复用器总线是复用器重构算法的核心。
--- 4.1节阐述复用器重构算法如何构建设计中的复用器树总线。4.2节的重构方法用于执行4.3节中定义的均衡算法。均衡增加了由压缩生成的有效4:1复用器的数量。
--- 第5节总结了在Altera Quartus II集成综合中运行的整个算法。第6节列出了来自120个Altera真实用户设计实例的基准测试结果,测试表明面积减少超过20%,平均节省了4.2%。
2. 背景知识
--- 2.1 复用器在设计中是怎样实现的
--- 行为级HDL设计中的任何条件代码通常会综合为复用器。本节阐述两个最常用的复用器生成代码实例。
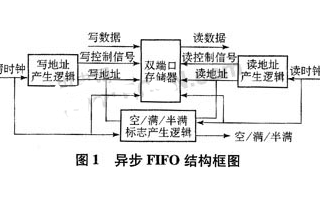
--- 图1是VHDL的case声明及其2:1复用器树的实现。采用Verilog case声明的“parallel case”指令[5]可产生相似的结果。
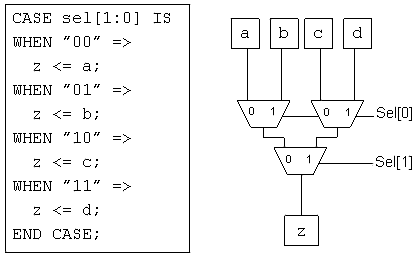
图1
--- 注意,并不是所有的case声明都能将可能的事件描述清楚,需要依靠“default”或者“others”条件来进一步说明。在这些情况下,可以继续将case声明表征为2:1复用器树,但是这种树结构可能达不到平衡。
--- 图2显示了“if-then-else”声明是怎样产生一个2:1复用器链的。Verilog的“?:”和非平行cases可同样产生相似的结构。注意,复用器链确保如果第一个if条件为“真”,将选择“a”数据输入,而复用器其他部分将被忽略。
--- 本文阐述的复用器重构算法应用于2:1复用器。综合工具由行为级代码开始通常会生成较大的复用器。较大的复用器总是被分解为2:1复用器树,如何实现这种分解已经超出本文讨论范围。
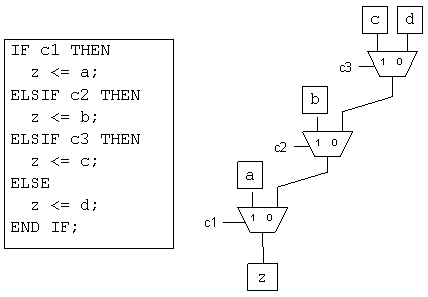
图2 if-then-else声明生成的逻辑 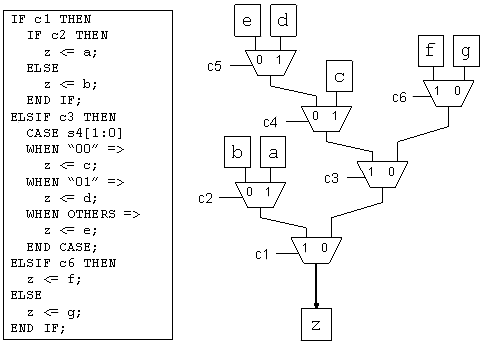
图3 HDL生成的复用器材 
图4 生成复用器总线
--- 2.2 复用器树
--- 设计中复用器之间的馈入是常见的现象。例如,在一段HDL代码中,如下面的图3所示,if-then-else声明中含有case声明就会产生这种现象。
--- 在复用器重构算法中,识别出较大的复用器树对于尽可能减少面积是非常重要的。
--- 2.3 复用器总线
--- VHDL信号或Verilog线宽通常会超过一个比特位。当采用if-then-else和case声明时,将会生成大量具有不同数据输入的相同复用器树,图4是一个实例。一组具有相同结构的复用器称为复用器树总线。
--- 本文阐述的复用器重构威廉希尔官方网站 采用了新的对整个复用器总线进行优化的方法,它通过由4.1节中进一步阐述的总线识别和形成威廉希尔官方网站 来实现。
--- 2.4 复用器代价
--- 在许多情况下,每个2:1复用器都需要一个单独的4-LUT。这样,图1和图2中的复用器结构都需要三个4-LUT。尽管这些结构控制编码不同,但是它们都具有4个不同的数据输入,因此可以当作4:1复用器。本节阐述如何实现只需要两个4-LUT的4:1复用器。
--- 图5是控制输入S0低电平时,一个有效的4:1复用器是如何工作的。4:1复用器由两个链接在一起的4-LUT(阴影框所示)构成。每个4-LUT被设置为含有阴影框中的逻辑功能。如白框所示,复用器含有四个输入——a、b、c和d,以及两个控制输入——S0和S1。

图5
--- S0低电平时,低位控制比特S1在输入c和d中进行选择,其结果通过第二个4-LUT,将a或者b输入旁路。

图6
--- 图6是控制输入S0高电平时,一个有效的4:1复用器是如何工作的。低位控制比特S1旁路c和d输入,直接进入第二个4-LUT,对a或者b输入进行选择,其结果成为第二个4-LUT的输出。
--- 第3节描述的压缩算法采用这种有效的4:1复用器,重新实现复用器结构,达到了减小面积的目的。
3. 压缩
--- 压缩是将低效的4:1复用器实现转换为高效实现的过程。复用器重构算法的面积节省由压缩实现。但是,在不同的复用器表征中进行转换,通常需要附加控制逻辑。实际上,由于附加逻辑结构抵消了使用高效复用器结构的优势,这种转换很少能够产生真正的面积节省。而复用器重构算法采用新颖的将整个复用器总线进行转换的方法,这样,总线上的多个复用器可以共享控制逻辑,因此,改善后的复用器结构优势可通过总线上的每个复用器来实现。
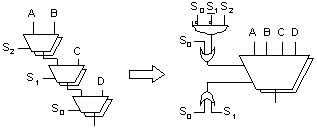
图7
--- 图7显示了如何将三个2:1复用器组成的优先级链转换为一个4:1二进制复用器。假设控制输入由不相关的逻辑馈入,那么这种转换至多需要两个额外的4-LUT控制逻辑。如果最初的复用器至少占用三个4-LUT,而4:1复用器只需要两个即可实现,那么这种转换将节省3宽度或者更宽总线的面积。
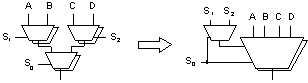
图8
--- 图8显示了如何将一组排列成树的2:1复用器转换为一个4:1复用器。在这种情况下,通过仔细为4:1复用器选择编码方式,使S0在(A、B)和(C、D)之间进行选择,限制附加控制逻辑,只加入最多一个4-LUT。此时,这种转换将节省2宽度或者更宽总线的面积。
--- 一般来讲,任何的三个2:1复用器组都可以通过图7或图8的方式转换为一个4:1复用器。但是,这两种转换必须在宽度大于2的复用器总线上进行,以减小所需4-LUT的数量,实际上,如果这两种转换不在总线上进行,将没有意义。
--- 总线上2:1复用器三联重新编码是复用器重构算法的核心。 第4节将阐述形成数量最多三联的新方法。
4. 复用器总线
4.1 “库”的构造
--- 压缩减小了其所编码的每一个2:1复用器三联面积,因此,压缩应用在较大的复用器树上最有效。本节阐述大型复用器树是如何构建的。设计中所有的总线都将被存储在一种称为“库”的数据结构中。
--- 复用器树采用下面的方法构建。设计中所有2:1复用器以反向深度顺序排列。这意味着那些离寄存器或者输出引脚最近的复用器将排在列表前面。然后从头至尾扫描列表,寻找每一个2:1复用器,如果其输出仅与另一个2:1复用器相连,则将该复用器和与其相连的复用器一起加到复用器树中。否则,将此2:1复用器作为一个新复用器树的首复用器。以此方式来构建的复用器树含有最大数量的复用器。
--- 如果复用器树中复用器的所有数据输入均不是由同一个树中其他的2:1复用器馈入,则称此复用器为初级输入(对整个树而言)。
--- 一旦所有的复用器树已经形成,则将其合并成总线。如果两个复用器树要并入同一个总线,它们必须具有相同的结构,即2:1复用器的排列相同,并且都有完全一致的控制输入。这可以通过根据复用器结构,对所有复用器树列表排序来实现,在列表中将结构相同的树靠近排列。总线可直接由结构相同的树构成。
--- 通过规则选取来实现总线宽度最大化。宽总线可以将由压缩引入的控制逻辑开销降低到最小。
--- 4.2 重构
--- 4.3节描述均衡方法,该方法能够使压缩得到的面积减小最大化。均衡建立在重构的基础上,其概念由本节给出。
--- 通过2:1复用器所馈入的一个2:1复用器,重构移动该复用器及其一个输入。图9显示了阴影复用器与其“f”输入的重构。为保持原始复用器总线的功能,需要附加一些控制逻辑。这些控制逻辑同样可以由总线上的每一个复用器树来分担。
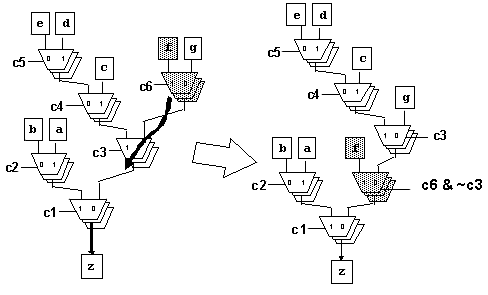
图9
--- 图9中,重新编码逻辑(c6 AND (NOT c3))必须确保当c1、c3为“假”而c6为“真”时,选择输入“f”(与转换前的情况一致)。同样,当c1、c3、c6为“假”时,选择输入“g”,即(c6 AND (NOT c3))也是“假”。
--- 重构转换将选中的复用器进一步向复用器树顶端移动。因此,不断重复重构转换,可以将任意位置的复用器向顶端移动。
--- 4.3 均衡
--- 压缩通过转换2:1复用器三联,能够减少实现复用器总线所需的4-LUT数量。但是,如果不进行复用器树重构,有些结构是不可能得到最佳三联分组的。例如,无法将图10中所有的2:1复用器进行分组,这是因为每一种可能的分组都将会剩余一个2:1复用器而无法处理。
--- 均衡的目的在于通过最少的重构得到最佳的压缩。对于图10的例子,可以采用图11所示的方法,得到两组2:1复用器三联。
--- 均衡算法由图12的递归定义。由首复用器开始,算法首先均衡复用器树左面和右面数据输入。均衡返回还没有连接为三联的2:1复用器的数量。均衡确保形成尽可能多的三联,这样只会剩余一个或者两个2:1复用器,甚至没有剩余。
--- 均衡中的任何阶段,都需要对1~5个2:1复用器进行均衡(从左侧分支开始最多两个,从右侧分支开始为两个,还要算上当前的2:1复用器本身)。1或2个复用器不会形成更多的三联,而3个复用器总是能够形成三联。4或5个复用器则需要进行重构,以免剩余无法处理的复用器,这种重构方法在图13和图14中示出。
图10 复用器树次优压缩的例子
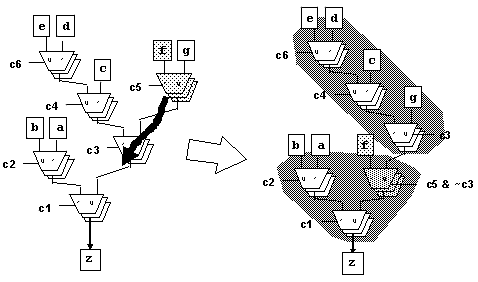
图11 由均衡未完善压缩

图12 均衡算法

图 13重构4个复用器实现均衡
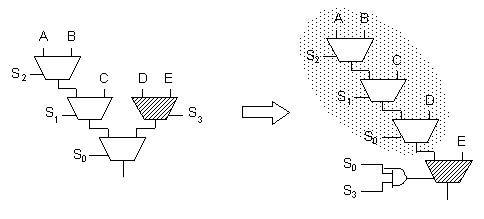
图14 重构5个复用器实现均衡
5. 算法总结
--- 本文引入了复用器树总线概念,描述了可用来提高压缩性能的均衡方法,压缩以效率更高的4:1复用器来替代2:1复用器三联。图15显示了全部复用器重构算法。
--- 复用器重构算法性能依赖于对较大复用器树总线的识别。由于复用器重构算法在整个总线上分担控制逻辑,因此,总线越宽,压缩的效果就越明显。优化会减小复用器树间的相似性,从而减小所寻找的总线宽度,因此在复用器重构之前,应尽量避免优化。
--- 复用器重构以分解大的复用器为2:1复用器开始。设计中所有2:1复用器都用于形成4.1节所描述的复用器树。结构相似的复用器树然后合并形成4.1节中的总线结构。
--- 算法的主要部分依次优化每一个总线。均衡将2:1复用器重新排列为三联,这样在压缩阶段,每个三联能够重新编码为效率更高的4:1复用器。
图16 复用器重构基准测试结果
6. 结果
--- 本文所阐述的算法已经集成到Altera Quartus II 4.2综合软件中。图16显示120个真实用户设计中,Altera基准测试的面积减小结果。
--- 结果表明,一小部分设计所需的LUT数量减小了20%,超过四成的设计面积减小了5%以上。所有设计面积平均减小了4.2%。
--- 据估算,面积减少平均4.2%意味着复用器平均减少了17%。
--- 复用器重构主要集中在减小面积上(例如,减少所需4-LUT的数量),而且对电路速率影响不大,电路平均速率仅降低1%。
7. 结论
--- 本文阐述了复用器重构算法,该算法能够将设计中实现复用器所需的4-LUT数量平均减少17%。
--- 复用器重构算法的关键在于优化复用器总线。即使附加了控制逻辑,新优化算法仍能够减小总线上每个比特位的面积。这是由于控制逻辑可以由总线共享,其面积代价可以抵消。
--- 压缩将2:1复用器三联转换为有效的4:1复用器。尽管可能需要附加LUT对4:1复用器控制线进行重新编码,这种代价可以通过采用复用器总线整体压缩方法来抵消。此外,通过构建最大的复用器树,可对大量的2:1复用器三联进行转换。
--- 本文还引入了能够提高压缩算法效率的均衡方法。本文描述了面向基于4-LUT的FPGA算法,例如Altera Stratix I和Cyclone器件。新的FPGA体系结构可使用不同大小的查找表(如Stratix II体系结构能够采用4、5、6输入LUT)。可采用本文阐述的方法来进一步减小这些体系结构的面积。
参考文献
1 A High Performance 32-bit ALU for Programmable Logic. P. Metzgen. Proceedings of the 2004 ACM/SIGDA 12th international symposium on Field Programmable Gate Arrays. Pp 61-70. 2004.
2 Logic Optimization Techniques for Multiplexers. J. Stephenson and P. Metzgen. Mentor User2User Conference 2004, www.mentor.com\user2user
3 The Stratix Device Handbook (Vol 1). Altera Corporation, 2004.
4 1076(tm) IEEE Standard VHDL Language Reference Manual. IEEE Computer Society. IEEE Std 1076(tm)-2002.
5 IEEE Standard Verilog(r) Hardware Description Language. IEEE Computer Society. IEEE Std 1364-2001.
 电子发烧友App
电子发烧友App























评论