摘要:作为一种常用的编码方式即哈夫曼编码,很多人在它的原理即应用方面都弄不不清楚,本文主要以哈夫曼编码原理与应用实例及算法流程图俩进一步说明。
哈夫曼编码定义
哈夫曼编码(Huffman Coding),又称霍夫曼编码,是一种编码方式,哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法,该方法完全依据字符出现概率来构造异字头的平均长度最短的码字,有时称之为最佳编码,一般就叫做Huffman编码(有时也称为霍夫曼编码)。
哈夫曼编码原理

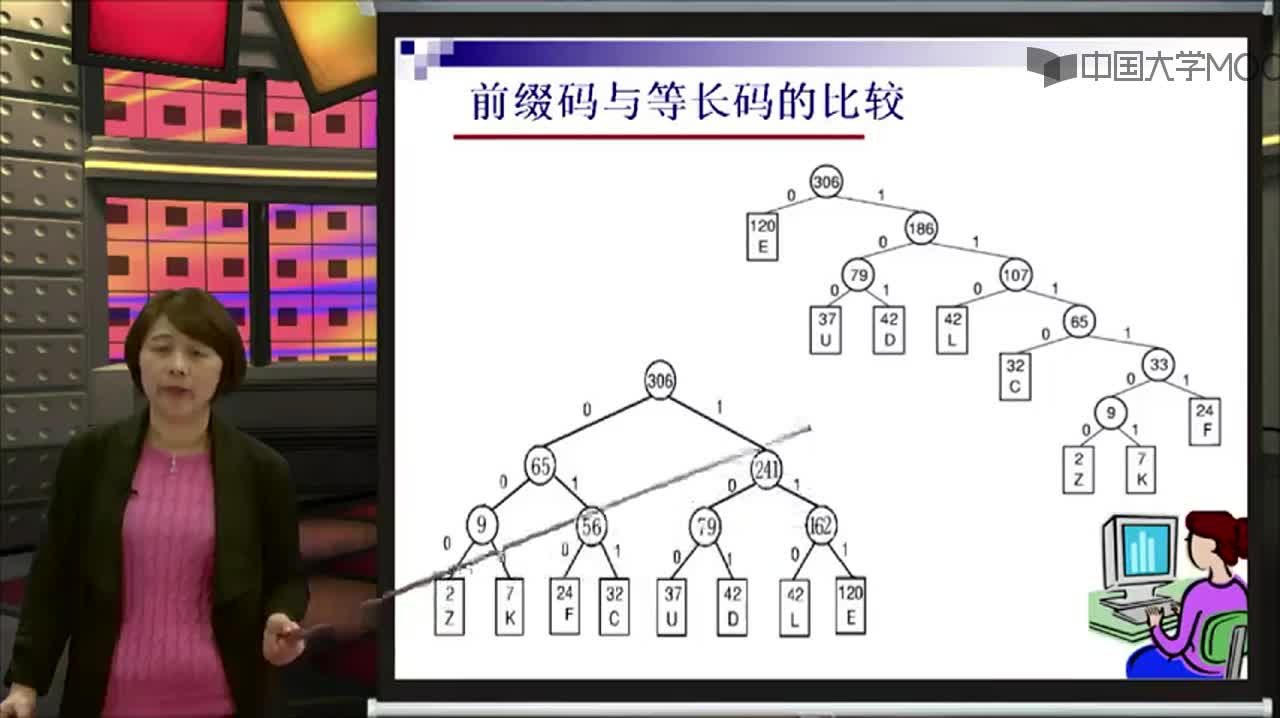
设某信源产生有五种符号u1、u2、u3、u4和u5,对应概率P1=0.4,P2=0.1,P3=P4=0.2,P5=0.1。首先,将符号按照概率由大到小排队,如图所示。编码时,从最小概率的两个符号开始,可选其中一个支路为0,另一支路为1。这里,我们选上支路为0,下支路为1。再将已编码的两支路的概率合并,并重新排队。多次重复使用上述方法直至合并概率归一时为止。从图(a)和(b)可以看出,两者虽平均码长相等,但同一符号可以有不同的码长,即编码方法并不唯一,其原因是两支路概率合并后重新排队时,可能出现几个支路概率相等,造成排队方法不唯一。一般,若将新合并后的支路排到等概率的最上支路,将有利于缩短码长方差,且编出的码更接近于等长码。这里图(a)的编码比(b)好。
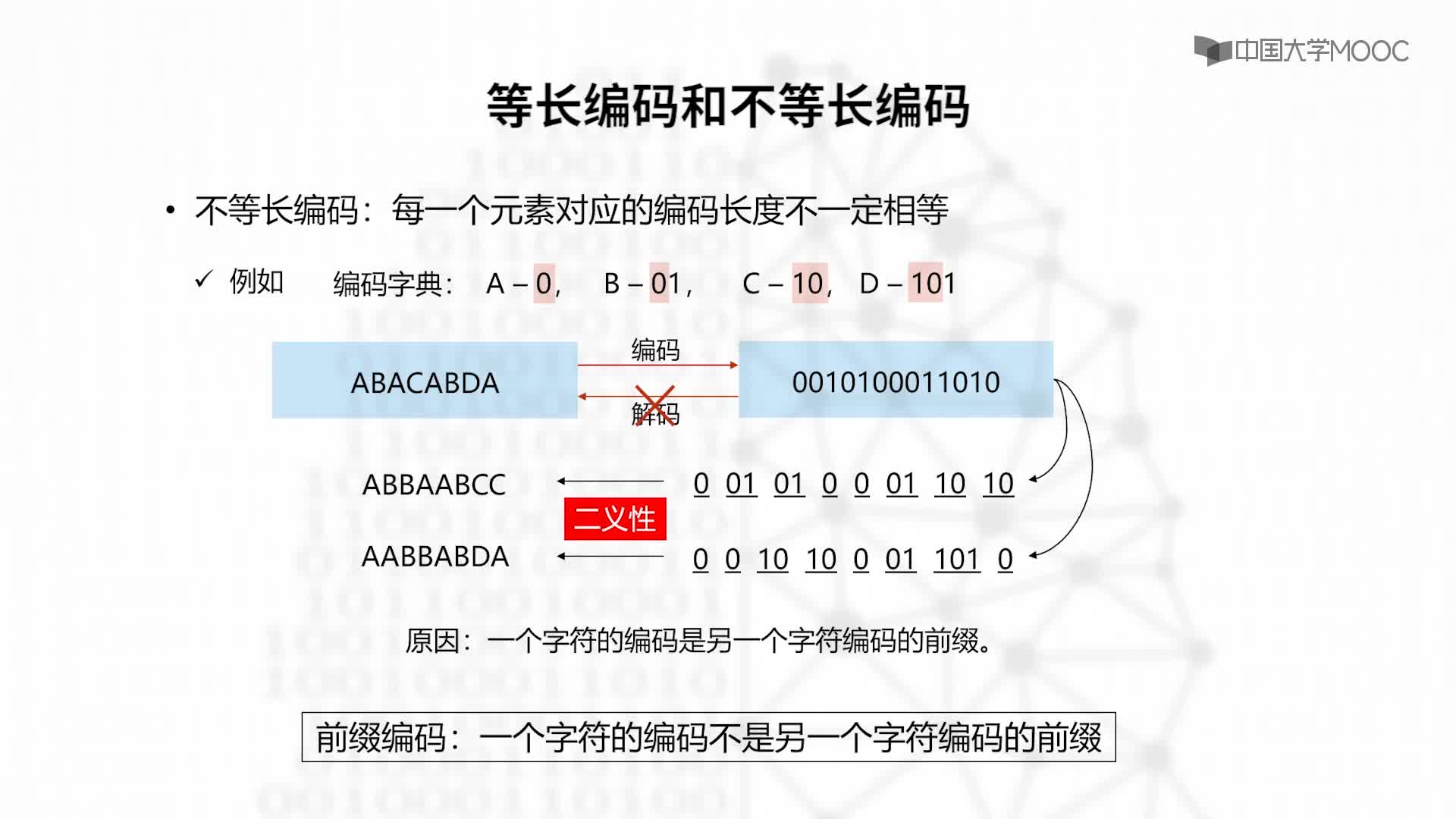
赫夫曼码的码字(各符号的代码)是异前置码字,即任一码字不会是另一码字的前面部分,这使各码字可以连在一起传送,中间不需另加隔离符号,只要传送时不出错,收端仍可分离各个码字,不致混淆。
实际应用中,除采用定时清洗以消除误差扩散和采用缓冲存储以解决速率匹配以外,主要问题是解决小符号集合的统计匹配,例如黑(1)、白(0)传真信源的统计匹配,采用0和1不同长度游程组成扩大的符号集合信源。游程,指相同码元的长度(如二进码中连续的一串0或一串1的长度或个数)。按照CCITT标准,需要统计2×1728种游程(长度),这样,实现时的存储量太大。事实上长游程的概率很小,故CCITT还规定:若l表示游程长度,则l=64q+r。其中q称主码,r为基码。编码时,不小于64的游程长度由主码和基码组成。而当l为64的整数倍时,只用主码的代码,已不存在基码的代码。
长游程的主码和基码均用赫夫曼规则进行编码,这称为修正赫夫曼码,其结果有表可查。该方法已广泛应用于文件传真机中。
哈夫曼编码算法流程图
哈夫曼编码的算法是查找最优路径的一种算法,首先在所有未分配parent域的节点中找出最小的两个节点,将他们的全值相加,组成新的节点,并且将它标记为原来两个最小节点的parent。这样调用递归,最后就能够成一颗完整的哈夫曼树。然后对 每个节点进行遍历编码,得到最终的哈夫曼编码库。流程图如下:

基于哈夫曼编码原理的压缩算法
哈夫曼算法的过程为:统计原始数据中各字符出现的频率;所有字符按频率降序排列;建立哈夫曼树:将哈夫曼树存入结果数据;重新编码原始数据到结果数据。哈夫曼算法实现流程如图3所示。

哈夫曼算法的实质是针对统计结果对字符本身重新编码,而不是对重复字符或重复子串编码。实用中.符号的出现频率不能预知,需要统计和编码两次处理,所以速度较慢,无法实用。而自适应(或动态)哈夫曼算法取消了统计,可在压缩数据时动态调整哈夫曼树,这样可提高速度。因此,哈夫曼编码效率高,运算速度快,实现方式灵活。
采用哈夫曼编码时需注意的问题:
(1)哈夫曼码无错误保护功能,译码时,码串若无错就能正确译码;若码串有错应考虑增加编码,提高可靠性。
(2)哈夫曼码是可变长度码,因此很难随意查找或调用压缩文件中间的内容,然后再译码,这就需要在存储代码之前加以考虑。
(3)哈夫曼树的实现和更新方法对设计非常关键。
哈夫曼编码应用实例
哈夫曼编码,主要用途是实现数据压缩。
设给出一段报文:CAST CAST SAT AT A TASA。字符集合是 { C, A, S, T },各个字符出现的频度(次数)是 W={ 2, 7, 4, 5 }。若给每个字符以等长编码A : 00 T : 10 C : 01 S : 11,则总编码长度为 ( 2+7+4+5 ) * 2 = 36。
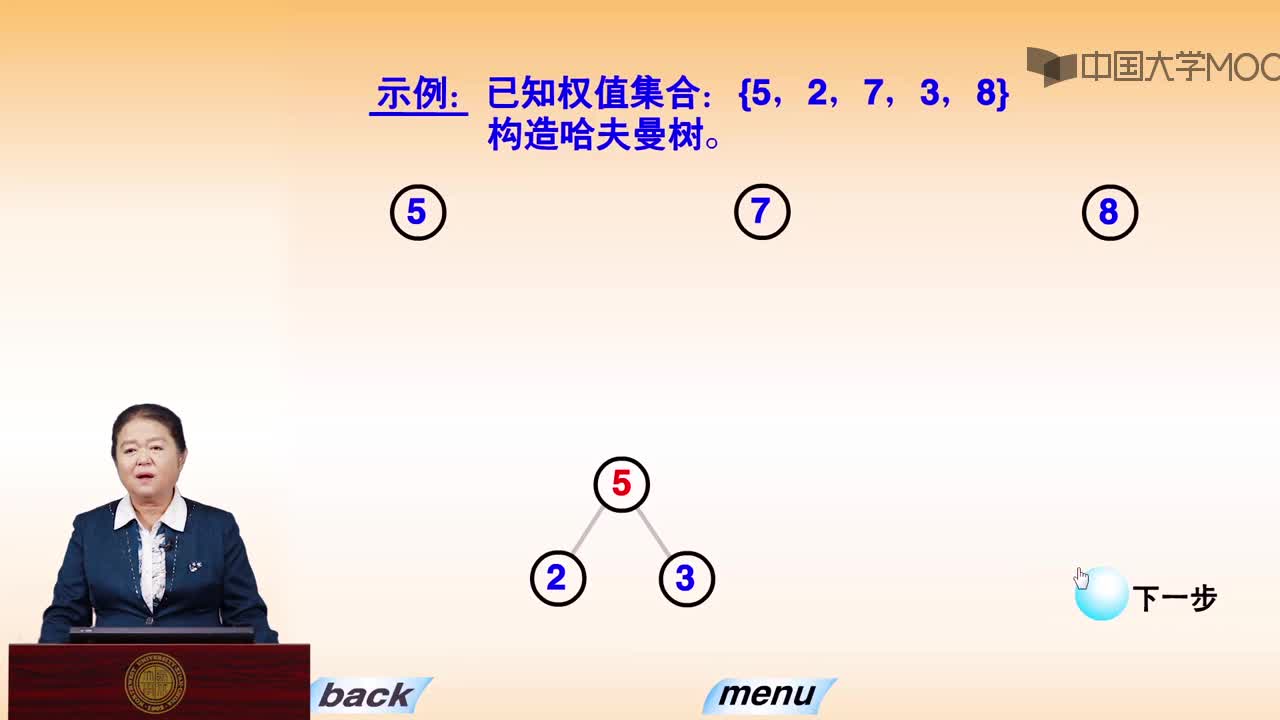
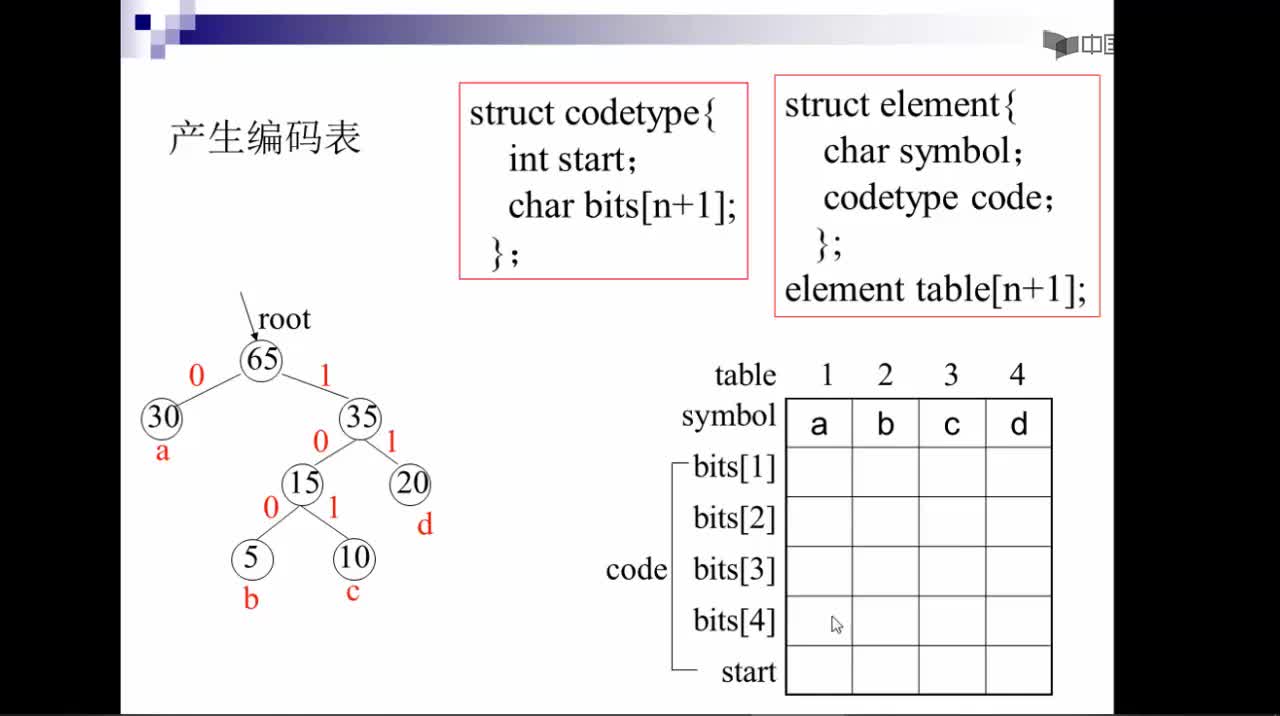
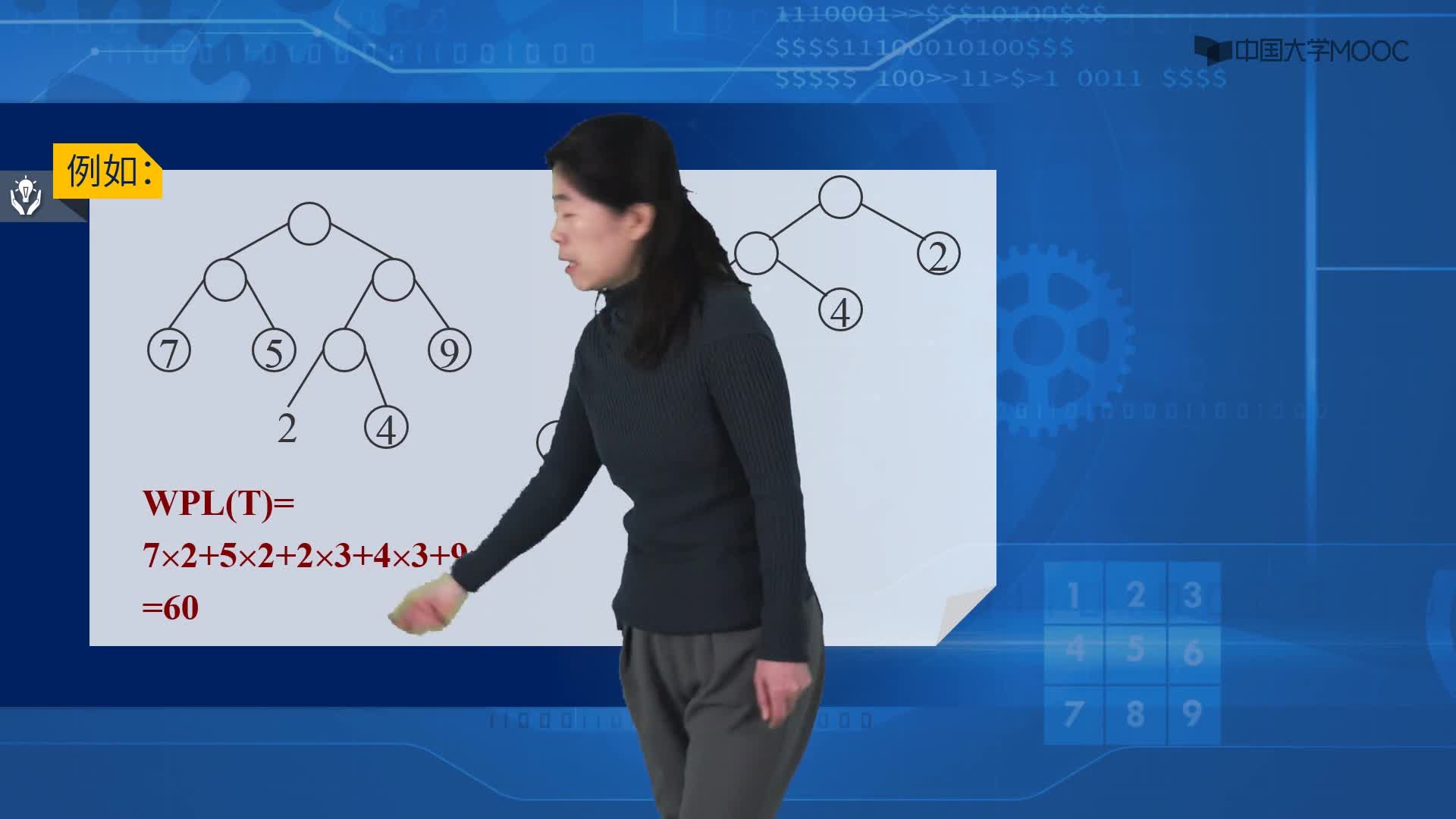
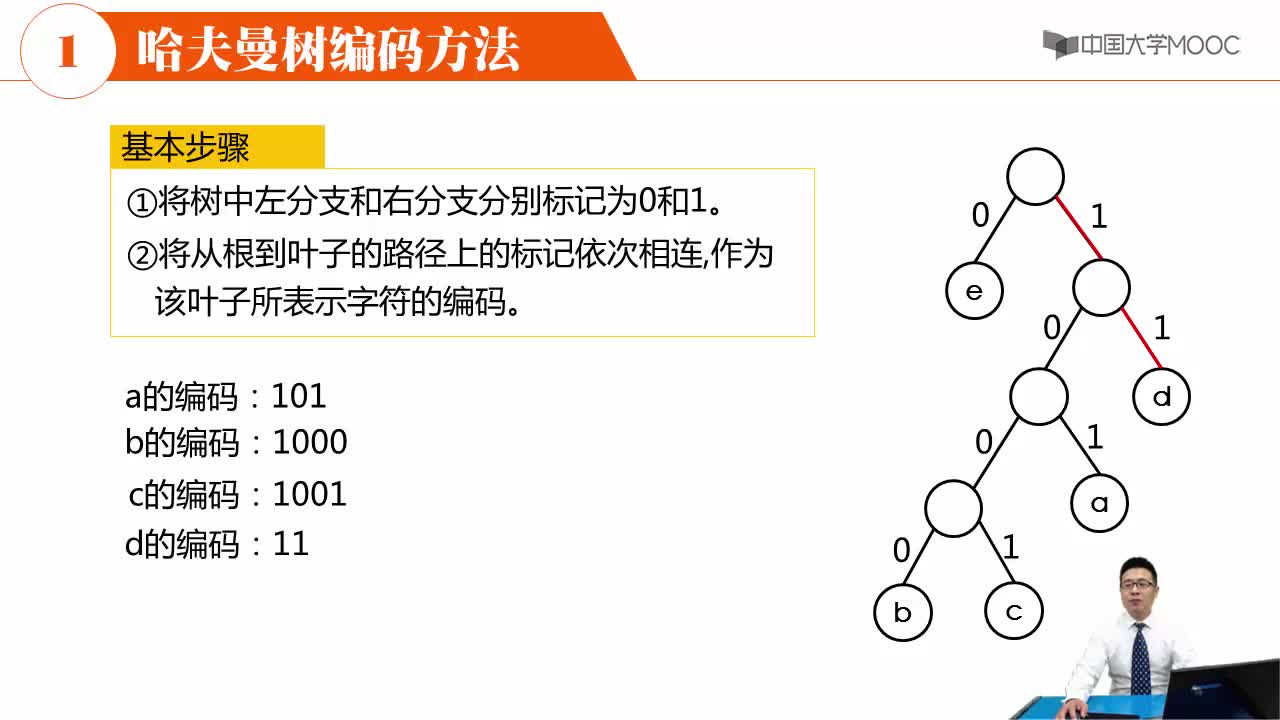
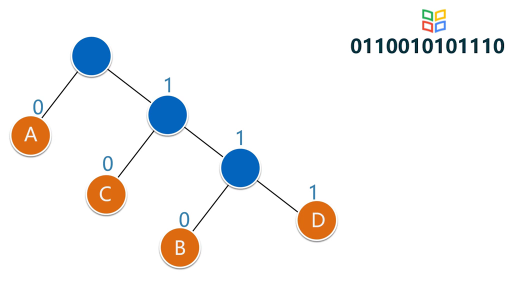
若按各个字符出现的概率不同而给予不等长编码,可望减少总编码长度。各字符出现概率为{ 2/18, 7/18, 4/18, 5/18 },化整为 { 2, 7, 4, 5 }。以它们为各叶结点上的权值, 建立霍夫曼树。左分支赋 0,右分支赋 1,得霍夫曼编码(变长编码)。A : 0 T : 10 C : 110 S : 111。它的总编码长度:7*1+5*2+( 2+4 )*3 = 35。比等长编码的情形要短。霍夫曼编码是一种无前缀编码。解码时不会混淆。带权路径长度达到最小的二叉树即为霍夫曼树。在霍夫曼树中,权值大的结点离根最近。
霍夫曼算法
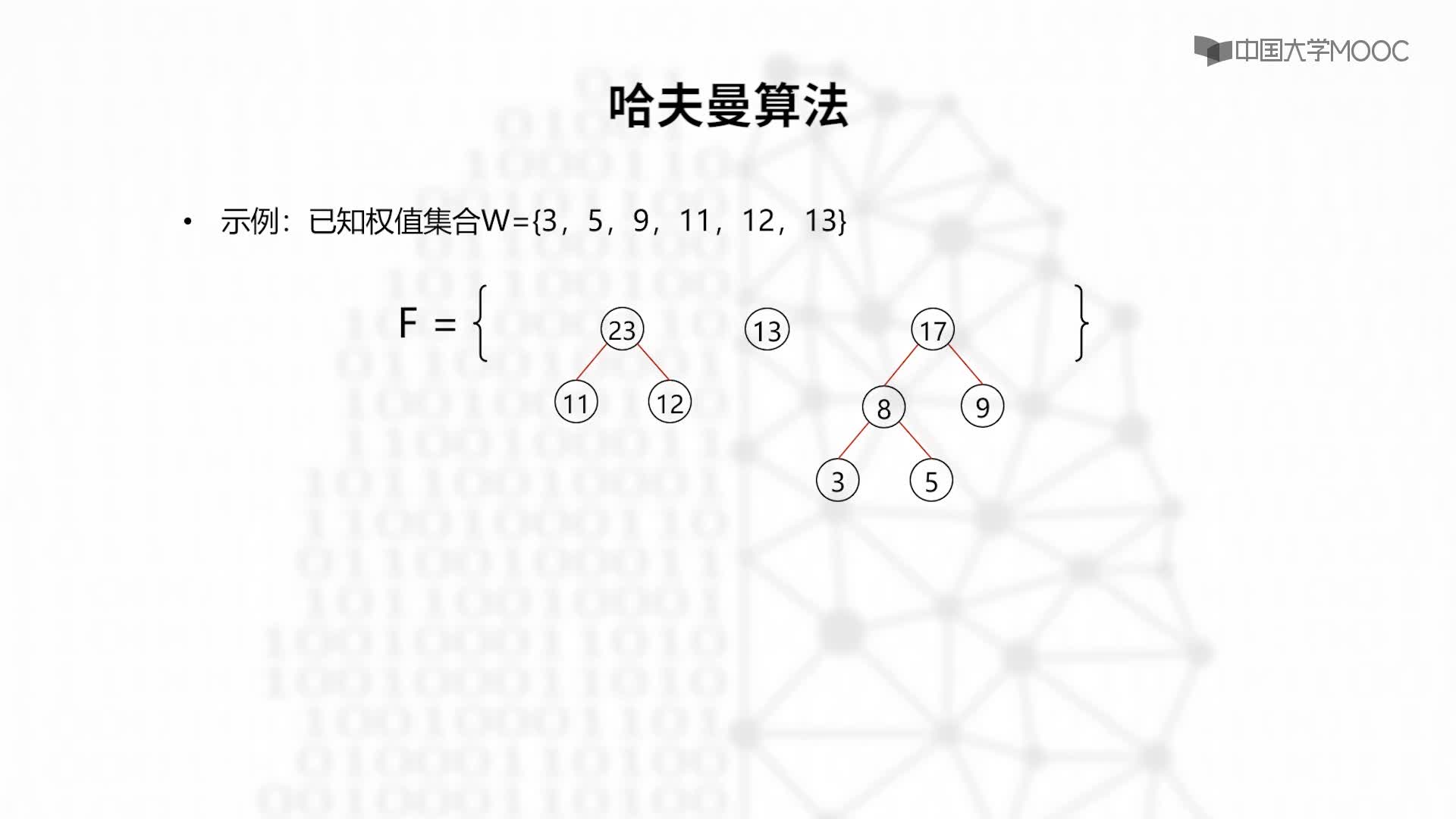
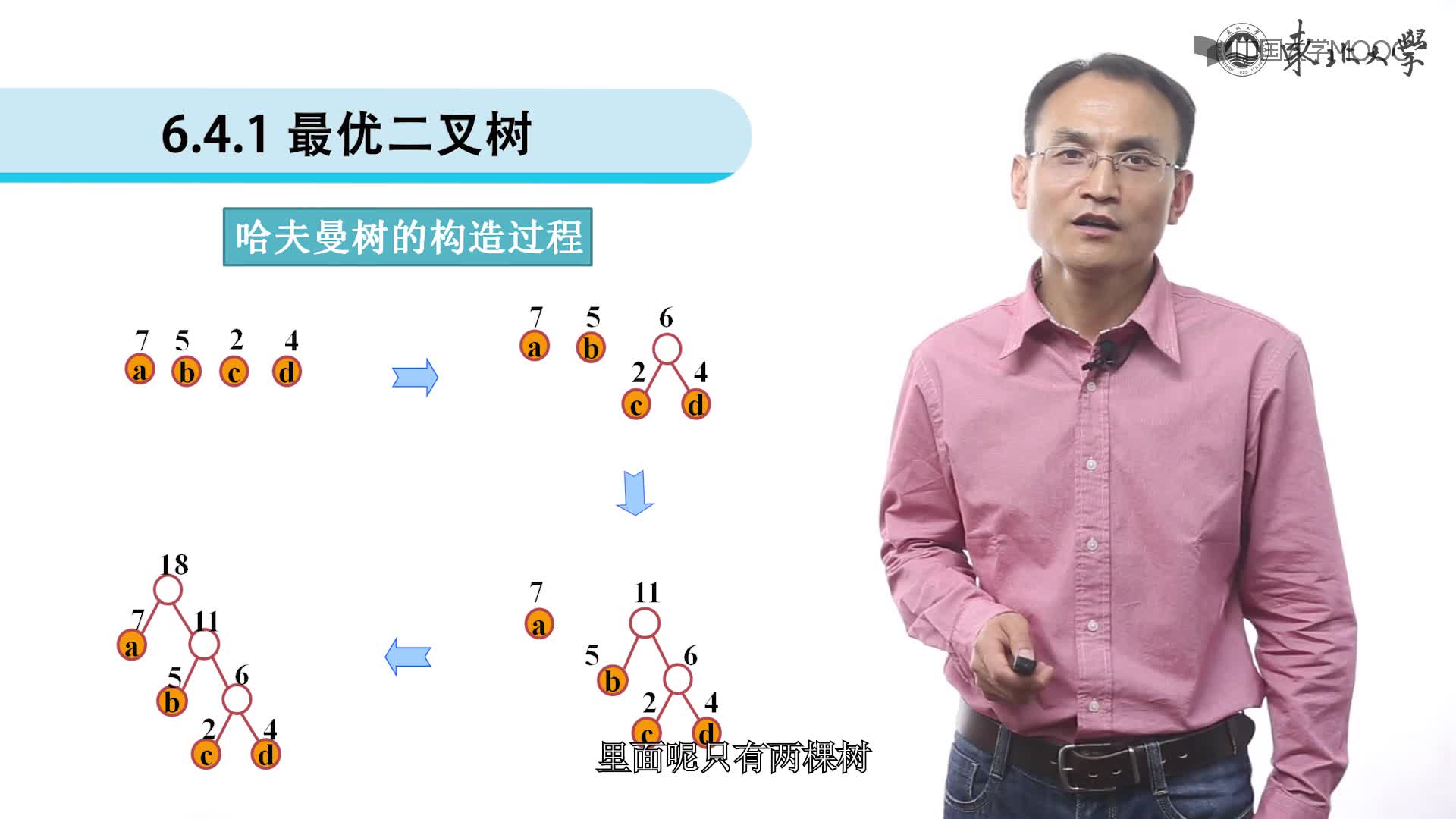
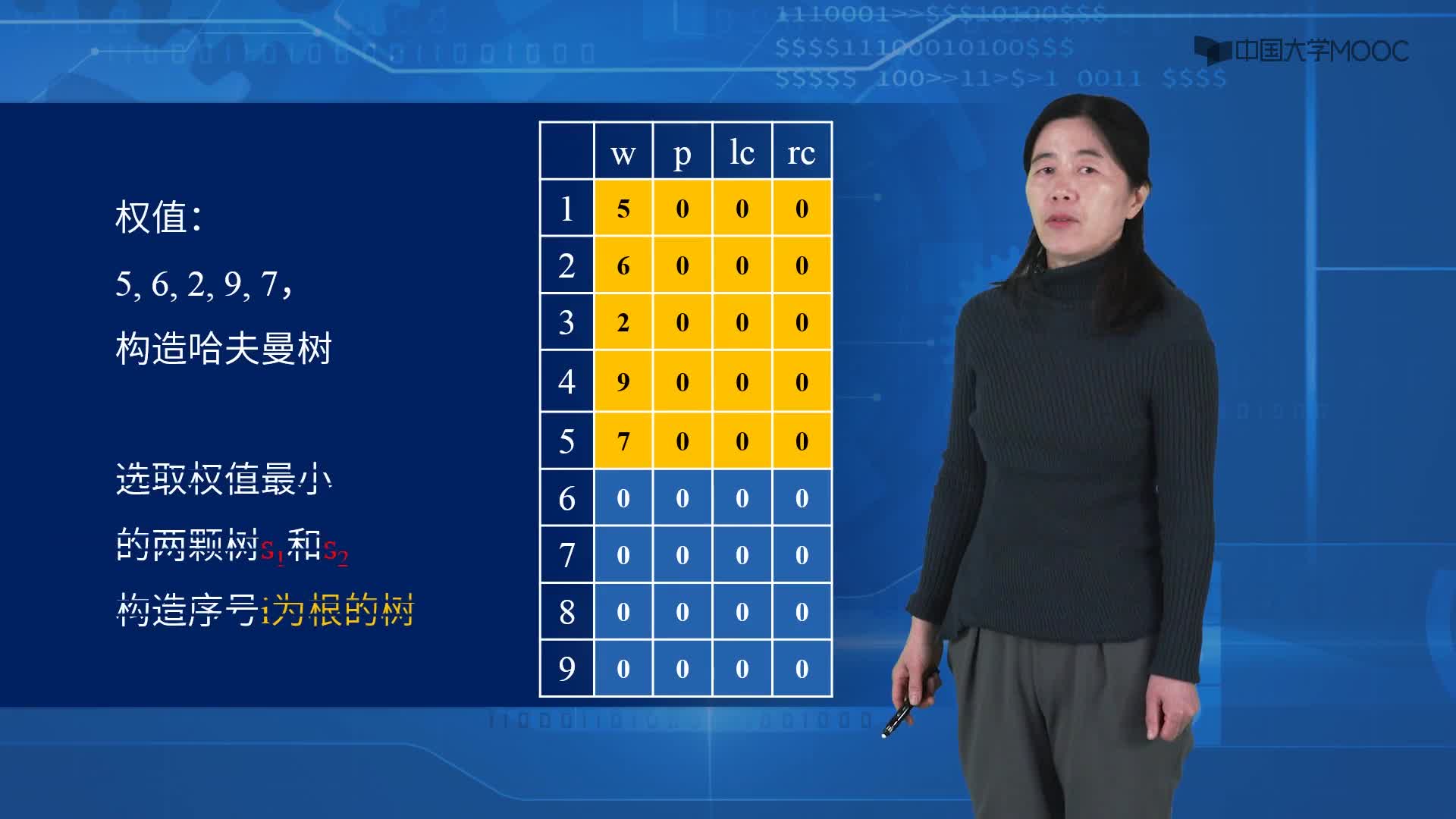
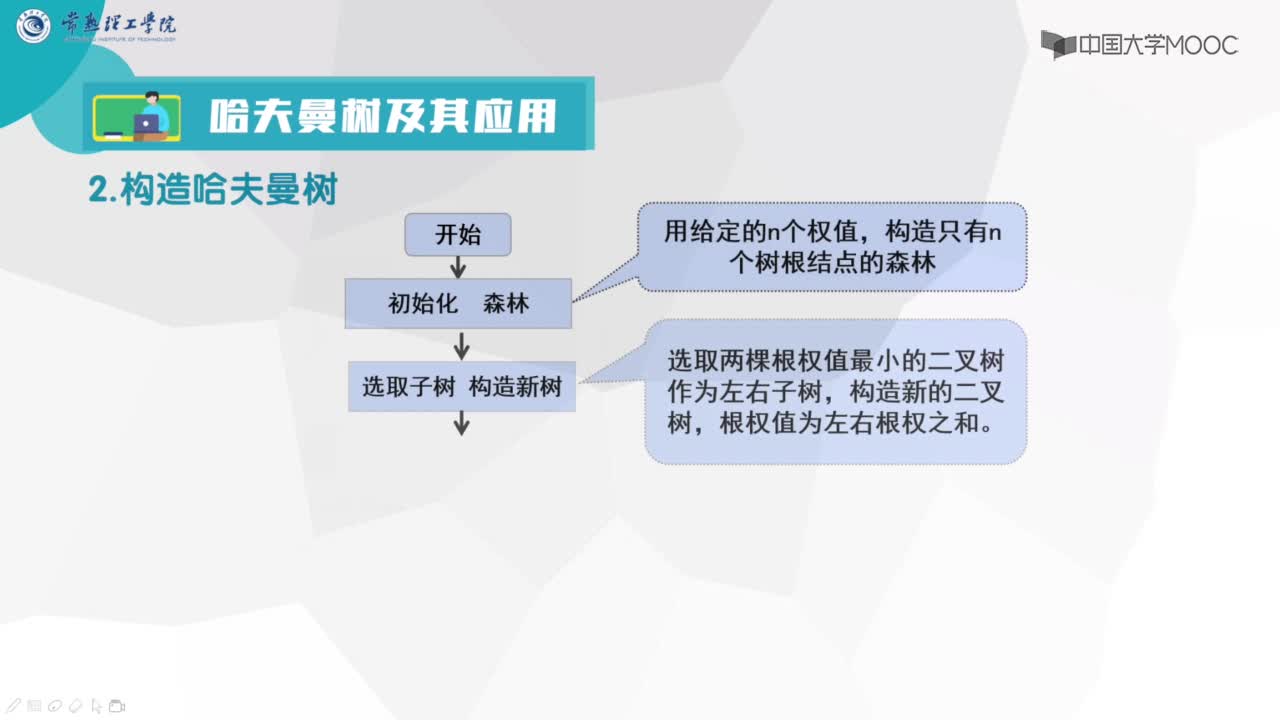
1.由给定的 n 个权值 {w0, w1, w2, …, wn-1},构造具有 n 棵扩充二叉树的森林 F = { T0, T1, T2, …, Tn-1 },其中每棵扩充二叉树 Ti 只有一 个带权值 wi 的根结点, 其左、右子树均为空。
2.重复以下步骤, 直到 F 中仅剩下一棵树为止:
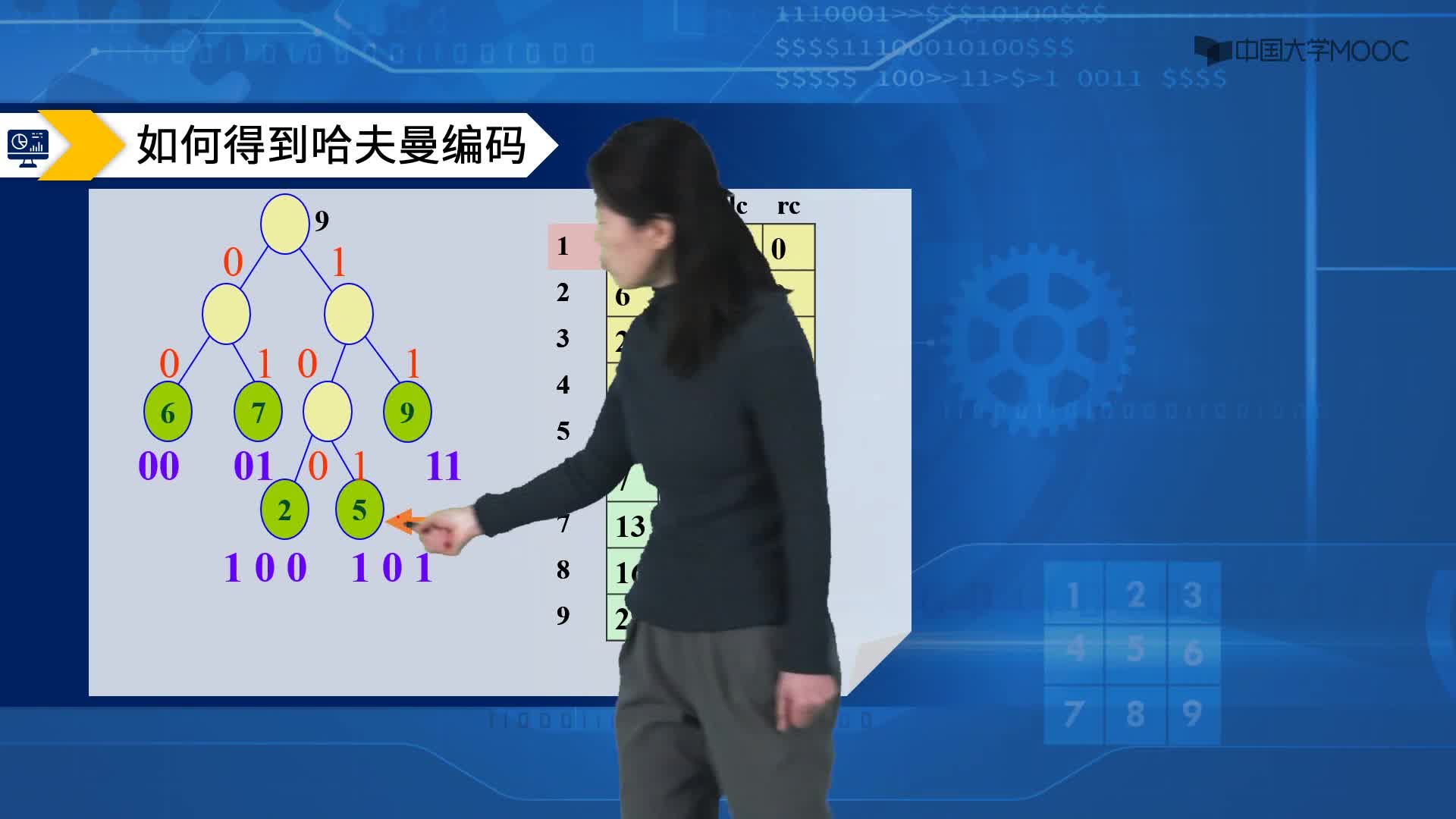
① 在 F 中选取两棵根结点的权值最小的扩充二叉树,做为左、右子树构造一棵新的二叉树。置新的二叉树的根结点的权值为其左、右子树上根结点的权值之和。
② 在 F 中删去这两棵二叉树。
③ 把新的二叉树加入 F。
#include 《stdio.h》
#include 《stdlib.h》
#include 《string.h》
#define MAX 32767
typedef char *HuffmanCode;
typedef struct
{
int Weight;//字母的权
int Parent,Leftchild,Rightchild;
}HuffmanTree;
void Select(HuffmanTree *HT,int n,int *s1,int *s2)
{
int min1=MAX;
int min2=MAX;
int pos1, pos2;
int i;
for(i=0;i《n;i++)
{
if(HT[i].Parent==-1)//选择还没有父亲的节点
{
if(HT[i].Weight《=min1)
{
pos2 = pos1; min2 = min1;
pos1 = i; min1=HT[i].Weight;
}
else if(HT[i].Weight《=min2)
{
pos2 = i; min2=HT[i].Weight;
}
}
}
*s1=pos1;*s2=pos2;
}
void CreateTree(HuffmanTree *HT,int n,int *w)
{
int m=2*n-1;//总的节点数
int s1,s2;
int i;
for(i=0;i《m;i++)
{
if(i《n)
HT[i].Weight=w[i];
else
HT[i].Weight=-1;
HT[i].Parent=-1;
HT[i].Leftchild=-1;
HT[i].Rightchild=-1;
}
for(i=n;i《m;i++)
{
Select(HT,i,&s1,&s2);//这个函数是从0到n-1中选两个权最小的节点
HT[i].Weight=HT[s1].Weight+HT[s2].Weight;
HT[i].Leftchild=s1;
HT[i].Rightchild=s2;
HT[s1].Parent=i;
HT[s2].Parent=i;
}
}
void Print(HuffmanTree *HT,int m)
{
if(m!=-1)
{
printf(“%d ”,HT[m].Weight);
Print(HT,HT[m].Leftchild);
Print(HT,HT[m].Rightchild);
}
}
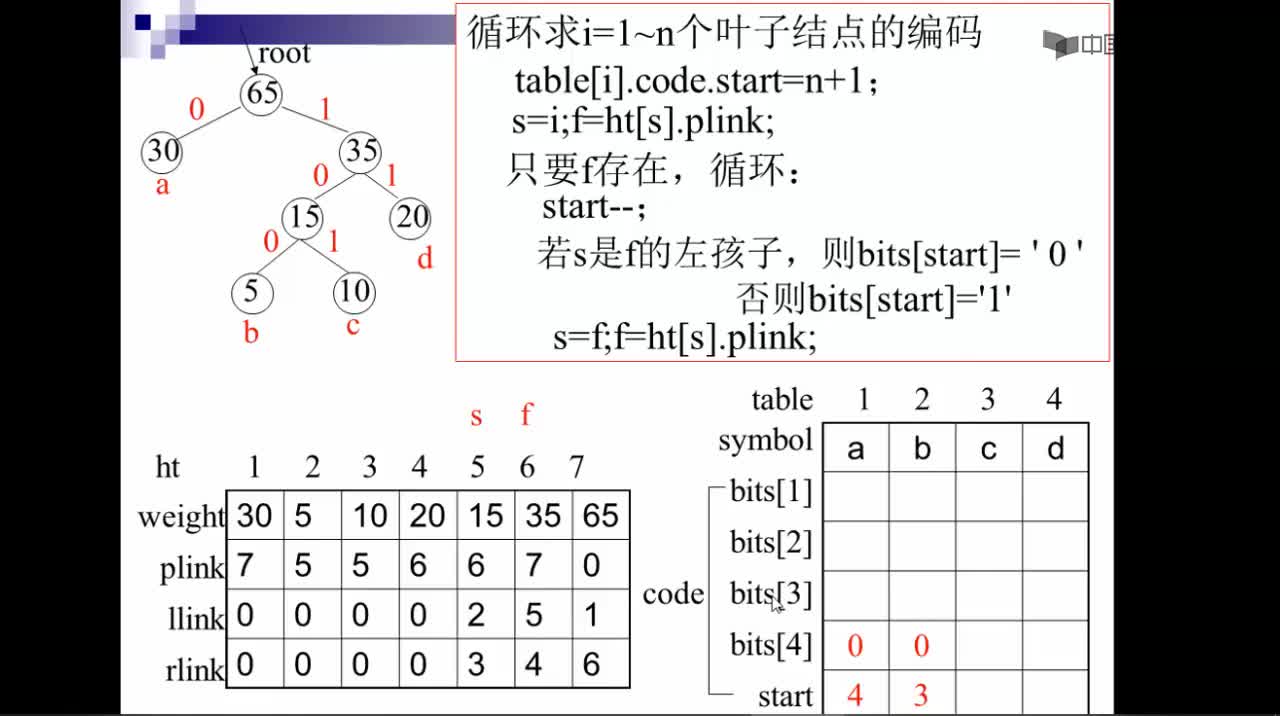
void Huffmancoding(HuffmanTree *HT,int n,HuffmanCode *hc,char *letters)
{
char *cd;
int start;
int Current,parent;
int i;
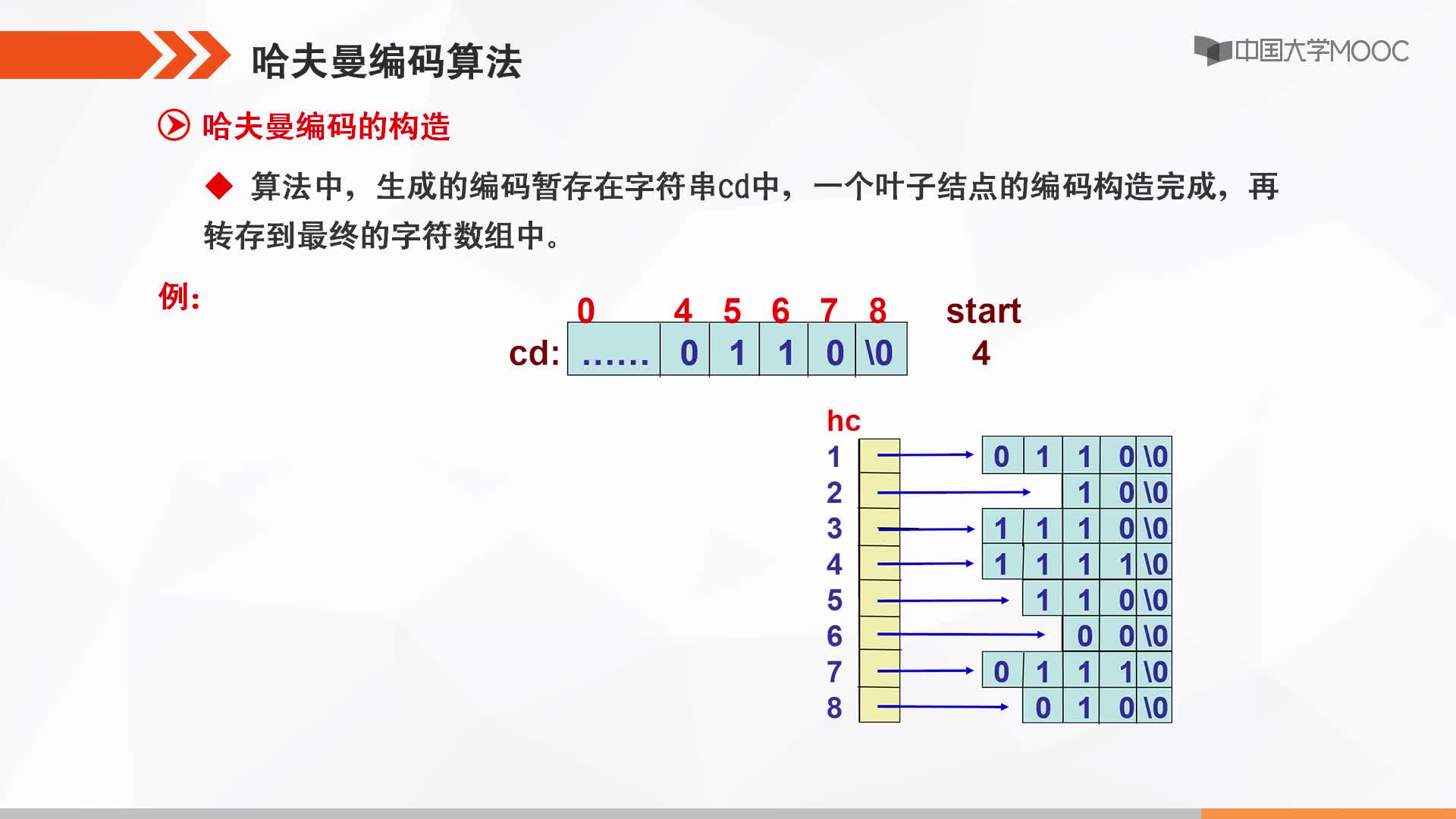
cd=(char*)malloc(sizeof(char)*n);//用来临时存放一个字母的编码结果
cd[n-1]=‘\0’;
for(i=0;i《n;i++)
{
start=n-1;
for(Current=i,parent=HT[Current].Parent; parent!=-1; Current=parent,parent=HT[parent].Parent)
if(Current==HT[parent].Leftchild)//判断该节点是父节点的左孩子还是右孩子
cd[--start]=‘0’;
else
cd[--start]=‘1’;
hc[i]=(char*)malloc(sizeof(char)*(n-start));
strcpy(hc[i],&cd[start]);
}
free(cd);
for(i=0;i《n;i++)
{
printf(“letters:%c,weight:%d,编码为 %s\n”,letters[i],HT[i].Weight,hc[i]);
printf(“\n”);
}
}
void Encode(HuffmanCode *hc,char *letters,char *test,char *code)
{
int len=0;
int i,j;
for(i=0;test[i]!=‘\0’;i++)
{
for(j=0;letters[j]!=test[i];j++){}
strcpy(code+len,hc[j]);
len=len+strlen(hc[j]);
}
printf(“The Test : %s \nEncode to be :”,test);
printf(“%s”,code);
printf(“\n”);
}
void Decode(HuffmanTree *HT,int m,char *code,char *letters)
{
int position=0,i;
printf(“The Code: %s \nDecode to be :”,code);
while(code[position]!=‘\0’)
{
for(i=m-1;HT[i].Leftchild!=-1&&HT[i].Rightchild!=-1;position++)
{
if(code[position]==‘0’)
i=HT[i].Leftchild;
else
i=HT[i].Rightchild;
}
printf(“%c”,letters[i]);
}
}
int main()
{
int n=27;
int m=2*n-1;
char letters[28]={‘a’,‘b’,‘c’,‘d’,‘e’,‘f’,‘g’,‘h’,‘i’,‘j’,‘k’,‘l’,‘m’,
‘n’,‘o’,‘p’,‘q’,‘r’,‘s’,‘t’,‘u’,‘v’,‘w’,‘x’,‘y’,‘z’,‘ ’};
int w[28]={64,13,22,32,103,21,15,47,57,1,5,32,20,
57,63,15,1,48,51,80,23,8,18,1,16,1,168};
char code[200];
char test[50]={“this is about build my life”};
HuffmanTree *HT;
HuffmanCode *hc;
HT=(HuffmanTree *)malloc(m*sizeof(HuffmanTree));
hc=(HuffmanCode *)malloc(n*sizeof(char*));
CreateTree(HT,n,w);
Print(HT,m-1);
printf(“\n”);
Huffmancoding(HT,n,hc,letters);
Encode(hc,letters,test,code);
Decode(HT,m,code,letters);
printf(“\n”);
return 0;
}
推荐阅读:
 电子发烧友App
电子发烧友App













































































评论