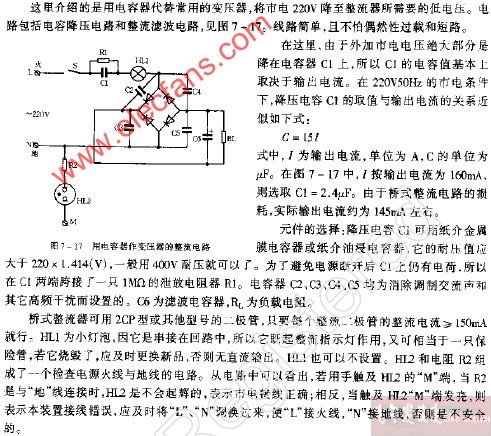
如何选用电容器

如何选用电容器

在电子电路中，尤其是与Hi-Fi有关的各种电路 包括HFIFAF 电容器使用的频度，大致上仅次于电阻器然电阻器使用虽多，而其作用 特性 种类却远较电容器为单纯，因为在一张线路图上，我们常常可以看到有关电阻规格的说明是 除特别说明外一律用碳膜1/2瓦，而电容器就没有那么方便了。

因为电容器的规格，除了电压 容量之外还有因结构不同而产生的种种形体及特性上的差异，若有选用错误，不仅电路不能工作，甚至于将发生危险包括损及其它零件和人体等 本文拟就以业余者为对象，叙述一般电容器的选用常识， 因编幅有限，是特将其较实用者优先论述。

一 电子电路中的电容器

电容器的基本作用就是充电与放电，但由这种基本充放电作用所延伸出来的许多电路现象，使得电容器有着种种不同的用途，例如在电动马达中，我们用它来产生相移，在照相闪光灯中，用它来产生高能量的瞬间放电等等，而在电子电路中，电容器不同性质的用途尤多，这许多不同的用途，虽然也有截然不同之处，但因其作用均系来自充电与放电，所以，在不同用途之间，亦难免有其共同之处，例如傍路电容实际上亦可称为平滑滤波电容，端看从哪一个角度来解释。

以下系就一般习惯的称呼做为分类，来说明电容器在不同电路中的作用和基本要求。

1.1  直流充放电电容

电容器的基本作用既是充电和放电，于是直接利用此充电和放电的功能便是电容器的主要用途之一 。

在此用途中的电容器，有如蓄电池和飞轮一般的功能，在供给能量高于需求时即予吸收并储存，而当供给能量低于需求或没有能量供给时，此储存的能量即可放出电容器充放电的作用与电池充放电的作用不一样，电池不管在充电或放电时，所需之作用时间均较长，因此，它无法在瞬间吸收大量的电能，也无法在瞬间放出大量的电能。

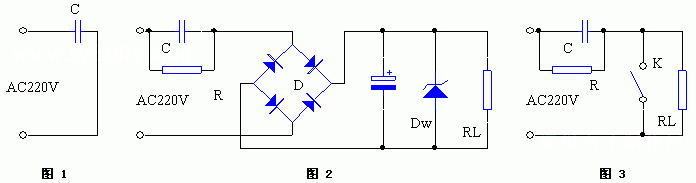
图1-1是常见的整流电路，图中二极管仅导通下半周的电流，在导通期间把电能储存于电容器上，在负半周时，二极管不导电，此时负载所需的电能唯赖电容器供给。

在此电路中，你可能想到，电容器在正半周所充之电能是否足够维持到负半迵使用 关于这个问题，有三个因素来决定 1.交流电在正半周时能否充份供应所需能量 2.电容器在正半周的充电期间，是否能够储存充份的能量 3.负载所需的平均电能是多少。

以上三个因素之中，1.2.数字若很大，而3.的需求则很小，即使在理论上亦无法获得纯粹的直流，因为电容器并非在正半周的全部时间都在充电，而只是在正半周的电压高于电容器既有的电压时，才有充电的作用在电容器不接负载时 漏电流亦不计，其充电的时间只是正半周的前四分之一周 电压上升时及至电压上升到峰值后，第二个正半周就不再充电了 当电容器接上负之后，开始放电，在不充电的时间内，放去了多少电能，在充电时才能回多少电能，正是因为这样，所以纹波是无法等于零的。

通常的整流充放电电路，都是在交流接近峰值的极短时间内充电，然后做稳定的 如前级放大器 或不稳定的 如B类放大器 放电，而放电之量亦仅占总电容量极小的部份 但也有少数电路中的电容是做长时间缓慢充电而后在瞬间大量放电的，这类电路例如照相用之闪光电路和点焊机中之放电电路等，其电容所要求的特性自与一般整流用电容不一样。

1.2  电源平滑滤波及反交连电容

前述的电源整流电路中的充放电电容，因有充电及放电时间之分，故必然会有纹波存在，为了尽可能降低纹波率，可如图1-2A另加一电容为C2，此电容即纯为平滑纹波之用，在图中A使用电感L为交连，B则为电阻交连，当使用L为交连时，有较高之效率，且设计适切时，有极佳之平滑滤波效果在图1-2中，如果整流后的负载是稳定的，例如是一只灯泡或一个蓄电池，则C2唯一之作用即为平滑滤波，然若此一电源供给器的负载并不稳定，那么在C2两端之电压，除了含有AC电源的纹波外，亦可能因负载变动而致电压有所起伏，起伏的幅度随负载变动幅度而异此时若以同一电源供给两个不同的负载，而其中又有一个负载对电压极为敏感时，那么第一个负载的电流变化，便可能影响第二个负载的动作，例如立体声两声道间的 串音，又如前后级共享电源而动作相位复为同相时可能引起之超低频振荡等为了防止类似这种来自电源的交连作用， 可在每一负载前单独加上一电容，此谓之反交连电容，如图1-2C之C2及C3。

1.3  高低通带通及分类

当电容器两端被加上极性不变的电压时，电容器就会充电，而此电压虽极性不变电压却随时改变时，电容器两端将保持最高电压值，这种现象，在前节中，我们己予叙述在本节中，我们想要讨论的乃是，当一只电容器的两被加上一电压和极性随时均在变化的压时，情况又是如何？

请看图1-3A当图中a点的电压对b点而言为正时，电容器做第一次充电，充电的方向是近a端为正，b端为负，在整个充电过程中，由于电容器内部原先无电能，而现在必须使它储存电能，所以必有电能消耗，虽然这种消耗被储存在一如蓄水池一样的电容器上，而无疑地，在电路内一定有电流流通，既有电流流通，就可以把电容器看成是导电的。

接着，当a点电压对b点而言到达正的最高值之后，又开始降低，此时由于图1-3A 的电路中没有像图1-2中一样的单向导电二极管，所以当a点对b点电压比电容器二端电压低时，电容器就开始放电，放电的方向当然和充电时的方向相反，既然有放电现象，就有电流，有电流，我们可以把电容器看成是导电的。

a点的电压一直下降，直到和b一样，，然后仍继续下降，此时a点的电压比b点的电压低，或者我们可以说a点对b点而言变成负的了于是电容器由放电动作变成反向充电，一直要延续到a对b而言到达最大的负值这整个过程 中，尽管a对b而言，经历了由正到负的变化，而对电容器的作用却只是a对b由高到低，方向并无改变，所以电容器由正向的放电一直到负向的充电，均维持着同一电流的方向当然，它也是导电的 而这个方向的导电作用一直要延续到a对b而言，越过最高的负值，使电容器做负向的放电。

在此整个状况的变化中，我们要注意三种现象 低电容器在整个电压变化的过程中所表现的，虽然都是可以导电的，然其导电的量，是否就是电源所能提供的最大的量呢这就未必了，例如电容器的容量若很小，在充电的时候，只能充少量的电，而放电时，也就将所充电能放完为止，所以可以想象电容量愈大，导电量也愈大 第二电容器充电是须要时间的，当电容量对电源所供给的能量而言，是很小的时候，电容两端的电压可以紧密地追随电源电压的变化，而电流却似乎是提前于电压变化90度，因此a由负到正时电流是一个方向，而由正的最大值到负的最大值又是一个方向，而电压则是由负到正再回到零为一个方向，越过零轴后才变换另一方向 第三也是在本节中所主要叙述的现象，也就是当电容量固定的时候，我们把电源变化的频率加快或减慢，其产生的情况将与电容量大小的变化是一样的，也就是当频率高时，相当于容量加大，所以它导电的量也愈大，反之电源频率低时，相当于容量减小，导电量也小。

导电量既有大有小，便有类于电阻的功能，但多少与电阻的导电性质有别，不同的情况是 电阻的导它仅与本身的阻值有关，而电容则除与容量有关外，还必须是交流，且与交流的频率有关我们把其中同与不同的部分综合之后，将电容的这种导电特性称之为容抗，容抗概念之确立因系来自与电阻值的对比，是故量度单位乃引用电阻值的单位 奥姆 Ohm或简作Ω。

容抗的公式是

Xc=1/2πfc

式中Xc是容抗值，单位为奥姆，f为所加交流频率，C为容量，单位为法拉。

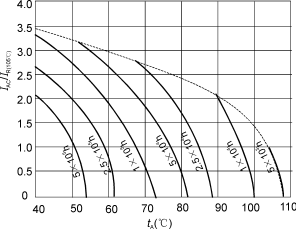
由上式，我们可以把一固定容量之电容器，求出其随频率变化的容抗，并绘成曲线，图1-3B即为0.1微法电容器的容抗曲线，我们可以发现1.容抗和频率反比 2.当频率为零 直流 时，容抗无限大 不导电。

利用电容器的这种容抗特性 如果把它串联在电路中 就可以使高频通过得多一点 而低频则通过得少一点 反之如把它并联在电路中则高频被削弱 因为短路掉了 得多一点 低频则削弱得少一点 串并联对电路发生的效果可以说正好是相反的。

但必须特别注意的是 单纯的电容虽有容抗产生 但无所表现 要使它有明确的表现 必须加入其它有别于电容的组件 例如电阻就是常加的组件之一。

我们且看图1-3C 如果AC电源之内阻非常的小 小于电容对该AC频率所呈容抗很多那么电容两端必完全呈现AC电源的它压 但假如AC电源有相当大的内阻大于电容对该AC频率所生容抗很多 则在电容两端因无足够的时间可以充电和放电 所以所呈现的AC电压几乎等于零 由以上两种极端的现象 我们发现电源的内阻将决定一既定容量之电容对一定频率的衰减情形 在实际使用中 由于电源或讯号源 的内阻并不是一项可以掌握的因子 所以通常设计时 必须将源阻设定得很低 然后以外加电阻与电容之配合 以达成控制频率之作用。

图1-3D所示为最简单之RC型高通或低通网络仔细地参看此二图 当可发现其基本结构并无不同 不同的只是电压的取出点不同而己 当电压是在电容两端取出时 频率愈高被衰减的就愈多 但电压在电阻两端取出时 频率愈高则衰减即愈少此即低通或高通网络 利用高 低通网络的混合组成 可以设计成某一特定频率范围才能通过网络 称之为带通网络 又利用高通 低通及带通的原理 将高 中 低不同的频率分别予以取出的就是分频网络。

1.4  傍路

假如在电路中 我们希望将某一频率以上或全部交流成份的信号予以去掉 那么我们便可以使用滤波电容 不过在习惯上 有少部份的电容滤波作用我们特称之为傍路电容 例如在晶体管的射极电阻或真空管的阴极电阻上并联的电容器 我们就叫它做傍路电容 因为其交流信号乃是经过此而入地之故 又如在电源电路中 除了数千微法的平滑滤波或反交连电容之外常亦用零点几微法的高频专用电容器来将高频傍路 实际上此高频傍路电容亦可视为高频滤波及反交连电容。

在1.3节中 我们曾经提到 电容器的导电情况 是在充电或放电完成以前所发生的作用所以电流先电压而产生 在电子电路中 有另外一种组件 电感 其特性正好与电容相反 也就是其电压先电流而发生 这两种特性相反的组件若予串或并联在一起 那么在某一特定频率时电容之电流导前和电感之电流落后 使两者正好重迭 于是电流变得最大 就成为电流谐振 反之电容之电流导前与电感之电流落后 使两者因互差180度而互相对消 电流就变成最小 此称为串联谐振。

串或并联谐振 通常被用于效率极高的带通或滤波网络之中。

1.6  振荡

电容器在导通交流电时 因电流和电压存在着相位差 所以在有增益的电路里 很容易产生振荡。

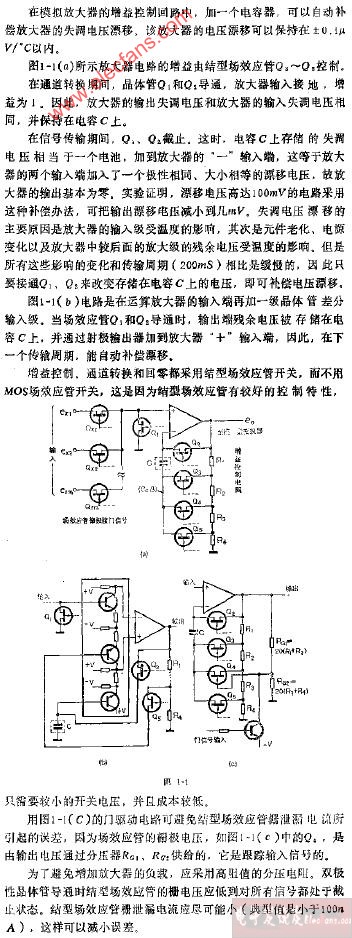
图1-6A即为一种移相振荡器图中的几个电容把 FET泄极间有增益 是故 周而复始的动作就产生了 这就是振荡。

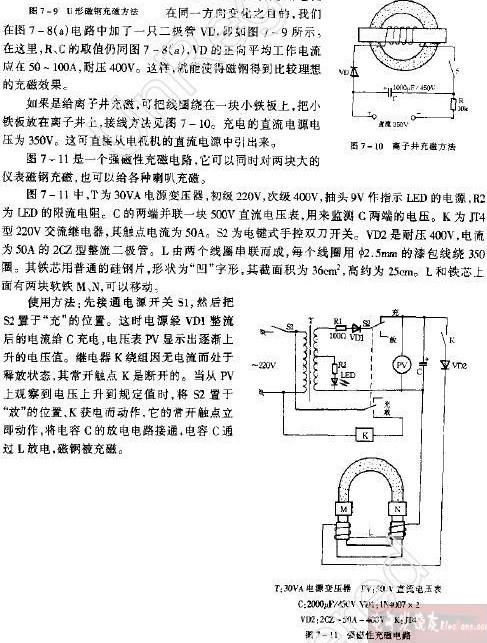
另外 使用一串联的RC接上一尼虹放电管时 也可以引发锯齿波振荡其动作的过程是 1.电源电压经由R到C充电 2. C电压逐渐升高 3.到尼虹放电管放电时电压时开始放电 4.继续放电 直到放电停止 5.又开始充电 以上动作之可能产生 其条件为 1.尼虹管之开始放电电压高于停止放电电压 2. R所能提供的持续电流小于尼虹管放电电流。

1.7  分压

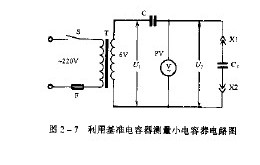
电容器对一特定频率之交流电 既会产生容抗 而容抗的性质又类于电阻 是故将两个容抗串联时 亦与电阻串联一样 会产生分压的作用由于容抗与容量成见于高频衰减器上如图1-7就是示波器或高频电压表输入电路中之衰减器 基本上乃以电阻为分压 衰减之基础 但为了减轻潜布电容对输入阻抗的影响 所以每一分压电阻均并上一电容 此电容量之间简易决定方法是使所有的R*C值均相等。

1.8  标准电容

和标准电阻一样 是被用于比较其它电容之用的特殊电容器 容量精确 质量极为安定 但售价亦非常高昂。

二 电容器的特性

2.1  电容器的构造

电容器既有如上一章所述的种种用途与功能 那么它的构造究竟如何 容量又是怎样形成的呢。

请看图2-1A设有两块金属片互相靠近但并不连接在一起 当此二金属片被加上电压时 由于正负电荷互相吸引 使得施加电压除去时 两金属片上仍维持着原有的电荷 这就是容电作用 就此简单的范例中 我们可以想象如果金属片相对的面积愈大 容纳电荷的面积就愈大 而金属片间隔愈小 电荷作用力愈强 所以以上两项因素可以决定电容量的大小。

2.2  介质与极化作用

上一节中我们所叙述的两片金属片互相靠近之后 所形成的电容 是假定两金属片间之间隙 没有任何其它物质存在 也就是以真空做为假想的。

在实际构造上 真空的结构自然是有些困难的 尤其是在真空而又必须维持一定间隙的时候 所以通常我们会在其间加入不导电的物质例如不将空气抽去时 中间便隔以空气 或如大多数的电容均使用云母 油纸或塑料膜为绝缘等。

当两极片间加上绝缘物质后 电荷是否仍然互相吸引呢 答案是仍然可以相互吸引 只是它们由直接的吸引变成了间接吸引此间接吸引之作用则来自绝缘物质内部的 极化作用 Polarization因为绝缘物质虽然不导电 但在其分子内部有等量的负电子和正电子正手 本来这些正负电子均呈杂乱无章的排列 形成平衡的局面 当此绝缘物质被介于两极片间时 极片的电荷吸引了这些电子 造成规则的同一方向的排列 一如铁分子受磁化的情形一样由是极片上的电荷作用经由这些排列整齐的电子而到达对方 使得绝缘物质在此变成了静荷的媒介体 故称此绝缘物质为介质。

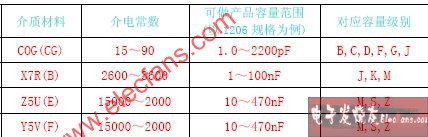
当二互相靠近的金属片间 加入介质之后其容量除受相对面积 距离影响之外 亦与介质之种类有关 如若以空气 真空 时之标准为1 不同介质对容量的影响称为介质系数 例如玻璃为4到7 石蜡为2 云母6到8 煤油2 纯水81 等等所以当我们想获得或制造一个容量很大的电容器时 必从三方面入手 一是加大相对面积 但体积会很庞大 二是缩小间隙 会造成绝缘不良 三使用介质系数较大的物质为介质 也要考虑物理及绝缘特性。

2.3  极化时间与适用频率

介质之极化作用并不是随静电场之产生而立刻发生的 换句话说 当二极片加上电压后必须等待一段反应时间 极化作用才能完成极化的时间当然很短 不过如果电容器要工作在高频率的时候 极化作用所需时间就是很重要的因素。

以不同的物质来担任介质 所需的极化时间并不一样 一般说来强极性化合物的极化时间较快 因为它在本极化前 分子己呈双极化而无极物质 Nonpo-lar Substance 则需先被诱导为双极性分子后 再极化之 不仅时间较慢 诱电率介质系数 亦低 是故不宜做为需容器之介质。

2.4  电容量

在2.1节中我们曾述及两金属片相对面积愈大或间隔愈小 均能使作用力依比例增加另外 亦能以选择适当的介质加强诱电效果 如以公式表之 即

在式中 为介质系数 是以真空时之介电常数所求出的各种介种常数 A为相对面积单位是平方公尺 d为距离 单位为公尺 C为电容量 单位为法拉 Farad简作F 又因在电子电路中 此基本单位的量太大了 所以常用微法拉或尼诺法拉或微微法拉。

一法拉的容量是指一伏特的电压加于电容器时 此电容器能储存一库伦Columb的电荷时的容量。

2.5  电容器的耐压

电容两端所施加之电压若提高 则其电荷亦增加 但是实际上此电压并不能任意加高 因为电容器二极片间之距离很小 电压升高后可能产生电昙 Corona即火花放电 而致电容遭到破坏 是故每一个电容器除了注明容量之外 工作电压也是一个非常重要的使用数据。

2.6  电容器的串并联

假如有单位面积之二金属片 形成一固定的电容量C 则此金属片之面积若增加为二单位时容量亦为2C 二单位面积之金属片未必一定是在一整大张面积 各单位间以导体互为连结 此称为电容器之并联。

电容器实施并联后 其总电容量为各并联电容量之和 亦即：

在某些特殊的情形下 电容器亦可串联使用 电容器串联使用 电容器串联时 串联容量之倒数为各容量之倒数和 亦即：

C = C1 + C2 + C3 …+ Cn

在某些特定的情形下 电容器串联使用 电容器串联时 串联容量之倒数为各容量之倒数和 亦即：

1/C = 1/ C1 + 1/ C2 + 1/C3 …+ 1/Cn

电容器实施串联后 会产生分压作用 其分压比为电容量之倒数比 因此虽施予直流电压 除非所有串联电容量均一样 否则串联后之总耐压值并非各耐压值之和。

2.7  电容器之等价电路

以上所述 均为一理想的电容器 亦即是只计电容不计其它。

 事实上电容器由于制造威廉希尔官方网站 或要求忽略等原因除了有容量之外 亦存在着并联的或串联的或串联的内电阻和串联电感 图2-7A即其等价电路。

电路中之g为漏电阻 乃因介质或封装材料之电导 绝缘电阻之倒数所引起 更清楚地说 就是介质或封装材料并不是绝对绝缘的 既非绝对绝缘 便有漏电 是故漏电流乃因漏电阻所产生 漏电流会消耗电能 并不是我们所需要的 但不同介质和结构会有不同的漏电流 在使用时 宜视实际要求而选定之。

图中之Rs为串联电阻 串联电阻值主要来自电极片和引线之实效电阻此电阻若不能忽略 那么电容器在充放电过程中 必因此而消耗一部份电能而变成熟 不仅虚耗功率 电容器本身亦易因熟而遭破坏。

计量串联电阻所产生的影响时 常以功率因子 Power factor或逸散因子 Dissipation factor的倒数来表示 然而在小容量 不做功率用途时 时 却以Q来表示 Q是逸散因子的倒数。

图中之Ls为串联电感 产生之原因主要是由于部份电容器之内部结构是由二长条的金属箔片间以介质后缠绕而成电感对交流电会产生感抗 它与容抗的相移特性正好相反 是故在高频工作时 串联电感的存在宜特别注意。