线性非时变系统定义给我们带来了许多数学工具,也包含卷积积分,傅里叶变换和拉普拉斯变换。
2023-10-17 10:31:46 122
122 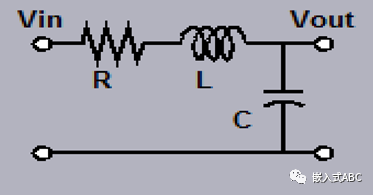
滤波器的响应可以用s域传递函数表示;变量s来自拉普拉斯变换,代表复杂的频率。
2023-09-19 16:58:07 481
481 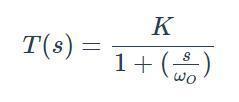
傅里叶变换与拉普拉斯变换的联系解读 傅里叶变换和拉普拉斯变换都是数学中非常重要的分析工具。它们都在不同的领域中发挥着重要作用。 傅里叶变换是一种将时间域信号转换成频率域信号的威廉希尔官方网站
。它是通过将信号
2023-09-07 17:04:19 219
219 如何用拉普拉斯变换分析电路 拉普拉斯变换是通过一种特定的方法将时域中的一个信号转化为复频域中的一个函数,从而使得复杂的微分方程等可以变得更加简单、易于求解。因此,它在电路分析中的应用非常广泛,有助于
2023-09-07 16:39:04 305
305 傅里叶变换拉普拉斯变换和z变换的区别联系 傅里叶变换、拉普拉斯变换和z变换是信号处理中重要的数学工具。傅里叶变换用于将一个连续时间信号转换为频域表示;拉普拉斯变换则用于将一个连续时间信号转换为复平面
2023-09-07 16:38:58 319
319 拉普拉斯变换公式 拉普拉斯变换公式是数学中极其重要的一种变换方式,它的应用领域非常广泛,包括在信号处理、控制论、微分方程、电路分析和量子力学等领域中都有着广泛的应用。本文将详细介绍拉普拉斯变换公式
2023-09-07 16:38:53 518
518 拉普拉斯变换的意义 拉普拉斯变换是微积分中的一种重要方法,用于将时间域函数转换为复平面的频域函数。它是工程和科学中常用的一种数学工具,尤其是电路理论、信号处理和控制理论中。 拉普拉斯变换的意义可以
2023-09-07 16:35:08 940
940 傅里叶变换和拉普拉斯变换的区别联系 傅里叶变换和拉普拉斯变换是数学中两种具有重要意义的变换方式。它们都在信号处理、传输和控制领域被广泛应用,能够将时域信号转换为频域信号或复平面上的信号。 傅里叶变换
2023-09-07 16:29:45 424
424 拉普拉斯变换的频移特性 拉普拉斯变换是一种重要的数学工具,在信号处理、控制理论、电路分析等领域广泛应用。在这些应用中,频移是一个常见的操作,即将信号在频域上移动某个频率。 拉普拉斯变换是一种复数变换
2023-09-07 16:29:43 141
141 第一部分 什么是卷积,卷积有什么用,什么是傅利叶变换,什么是拉普拉斯变换?
2023-04-12 10:58:53 923
923 之前的一阶电路和二阶电路的分析,所应用的方法是根据电路定理和元件的电压,电流关系建立线性常微分方程,通过求解微分方程的解求得电路的时域响应,这种方法又称为经典法。
2023-03-10 10:47:46 1532
1532 
所以对于高阶系统,一般采用积分变换法,将时域函数变为频域函数,从而将时域微分方程转为频域代数方程求解,求出频域解后在还原为时域解。拉普拉斯变换是一种重要的积分变换。
2023-03-02 14:19:27 591
591 
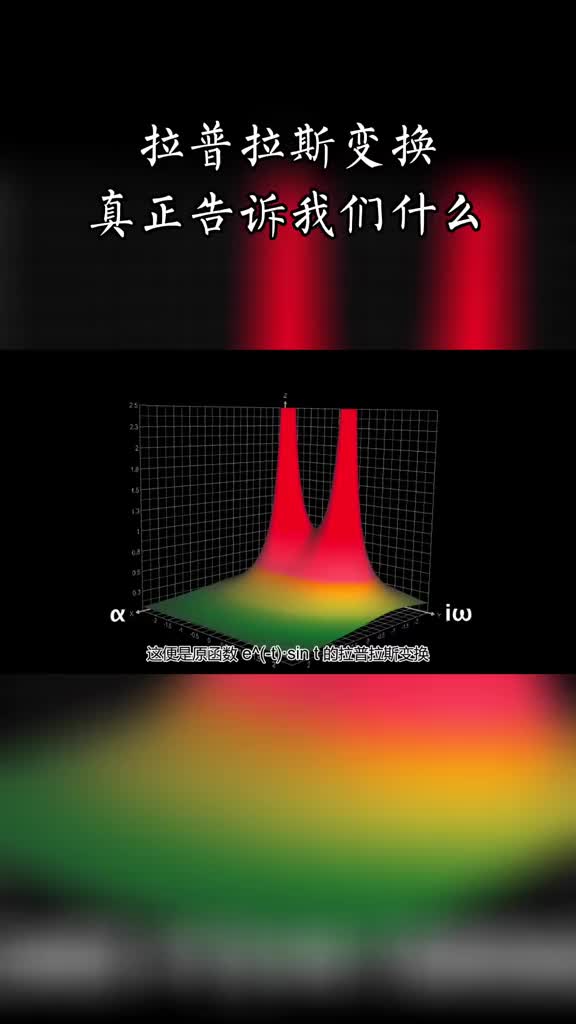
傅里叶变化只能对能量有限的信号进行变换(也就是可以收敛的信号),无法对能量无限的信号进行变换(无法收敛),因此,拉普拉斯应运而生,在原先的傅里叶变换公式中乘以一个衰减因子,使得无限能量的信号也能进行时频变换。
2022-11-28 11:00:23 1013
1013 数学变换是指数学函数从原向量空间在自身函数空间变换,或映射到另一个函数空间,或对于集合X到其自身(比如线性变换)或从X到另一个集合Y的可逆变换函数。
2022-07-23 17:45:10 1785
1785 
赫维赛德之所以这么做,是因为他的“物理直觉”告诉他这么做,就是这么硬。这显然是一种开外挂的行为,因此也受到当时的主流数学家们们的攻讦,他们认为赫维赛德就是十足的“民科”,文章没什么理论依据,自己在那空想呢。当然,赫维赛德也不是弱鸡,科学家怼起人来,也是毫不含糊:“因为我不能理解消化过程就拒绝晚餐吗?不,只要我满意这个结果。”
2022-03-15 14:08:18 1611
1611 信号与系统.PDF书,讲述了拉普拉斯变换、Z变换与傅里叶变换方便的知识,通俗易懂。
2022-01-07 09:21:05 5
5 拉普拉斯变换表下载
2021-12-30 09:47:12 4
4 从傅里叶级数、傅里叶变换推出拉普拉斯变换。
2021-06-23 16:25:27 5437
5437 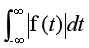
拉普拉斯变换.ppt以傅立叶变换为基础的频域分析方法的优点在于:它给出的结果有着清楚的物理意义 ,但也有不足之处,傅立叶变换只能处理符合狄利克雷条件的信号,而有些信号是不满足绝对可积条件的,因而
2009-09-16 08:35:50
电子发烧友网为你提供通俗的角度看待拉普拉斯变换资料下载的电子资料下载,更有其他相关的电路图、源代码、课件教程、中文资料、英文资料、参考设计、用户指南、解决方案等资料,希望可以帮助到广大的电子工程师们。
2021-03-30 08:47:41 6
6 在知乎上看到一个问题,傅里叶变换、拉普拉斯变换、Z 变换的联系是什么?为什么要进行这些变换?我觉得这是一个非常好的问题,貌似一下子也回答不上来,所以整理学习并分享一下。
2021-02-15 11:59:00 7844
7844 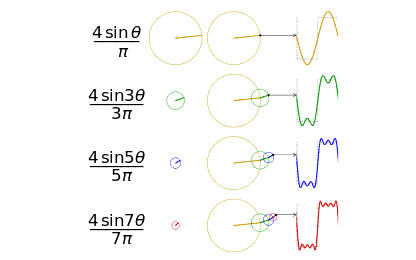
数学变换是指数学函数从原向量空间在自身函数空间变换,或映射到另一个函数空间,或对于集合X到其自身(比如线性变换)或从X到另一个集合Y的可逆变换函数。
2021-01-18 16:13:41 2976
2976 
傅里叶变换在物理学、数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学、海洋学、结构动力学等领域都有着广泛的应用(例如在信号处理中,傅里叶变换的典型用途是将信号分解成幅值分量和频率分量
2020-11-17 10:38:00 1
1 本文档的主要内容详细介绍的是拉普拉斯变换的习题与详解免费下载。
2020-09-28 08:00:00 0
0 本文档的主要内容详细介绍的是控制系统的数学模型拉普拉斯变换的详细资料说明。
2020-06-09 08:00:00 0
0 Z变换和傅里叶变换之间有存在什么样的关系呢?傅里叶变换的物理意义非常清晰:将通常在时域表示的信号,分解为多个正弦信号的叠加。
2019-09-29 07:05:00 5245
5245 傅里叶变换在物理学、数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学、海洋学、结构动力学等领域都有着广泛的应用(例如在信号处理中,傅里叶变换的典型用途是将信号分解成幅值分量和频率分量)。
2019-03-08 15:01:06 5960
5960 本文档的主要内容详细介绍的是拉普拉斯变换电路理论练习题来做作看吧。
2018-11-27 08:00:00 15
15 拉普拉斯变换是工程数学中常用的一种积分变换,又名拉氏变换。拉氏变换是一个线性变换,可将一个有引数实数t(t≥ 0)的函数转换为一个引数为复数s的函数。
2018-09-17 08:02:00 11315
11315 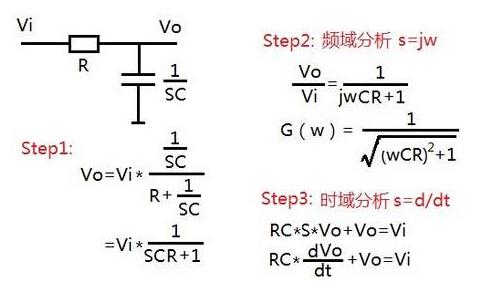
傅里叶变换与拉普拉斯变换的物理解释及区别pdf文档资料下载
2017-12-19 17:22:52 4
4 拉普拉斯变换是工程数学中常用的一种积分变换,又名拉氏变换。拉氏变换是一个线性变换,可将一个有参数实数t(t≥ 0)的函数转换为一个参数为复数s的函数。拉普拉斯变换在许多工程威廉希尔官方网站
和科学研究领域
2017-12-06 17:22:46 76342
76342 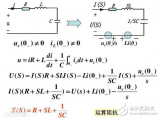
一种积分变换,它来源于函数的傅里叶积分表示。积分称为ƒ 的傅里叶积分。拉普拉斯变换是工程数学中常用的一种积分变换,又名拉氏变换。拉氏变换是一个线性变换,可将一个有参数实数t(t≥ 0)的函数转换为一个参数为复数s的函数。
2017-12-05 19:10:02 83345
83345 
有些情形下一个实变量函数在实数域中进行一些运算并不容易,但若将实变量函数作拉普拉斯变换,并在复数域中作各种运算,再将运算结果作拉普拉斯反变换来求得实数域中的相应结果,在经典控制理论中,对控制系统的分析和综合,都是建立在拉普拉斯变换的基础上的。
2017-12-05 18:30:31 234698
234698 
传递函数是指零初始条件下线性系统响应(即输出)量的拉普拉斯变换(或z变换)与激励(即输入)量的拉普拉斯变换之比。延迟环节从输入开始后在0 ~ τ时间内没有输出,但t =τ之后,输出完全等于输入。
2017-11-29 16:40:18 61938
61938 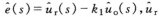
关于利用拉普拉斯变换求解系统初值问题书中只给出了一种比较简单的情况,即时域函数在零时刻有界时的求解方法。很遗憾,对于在零时刻存在冲击情况下的初值问题,这种方法并不适用。而这种问题又是大量存在的,所以
2017-11-16 11:02:22 5
5 自动化基础知识--拉普拉斯变换的概念
2017-10-26 08:53:36 1
1 拉普拉斯变换及其应用拉普拉斯变换及其应用拉普拉斯变换及其应用拉普拉斯变换及其应用
2015-10-28 11:19:28 26
26 2014-09-06 22:26:19 5
5 2013-12-18 12:07:19 1
1 2012-06-06 15:14:45 30
30 应用拉普拉斯变换分析RLC电路:应用拉普拉斯变换分析R上c 电路,不需要确定积分常数,从而避免了时域求解微分方程确定积分常数的繁琐计算。关键词:拉普拉斯变换;RLC电路
2010-04-12 08:31:44 124
124 z变换与拉普拉斯变换的关系:一.z平面与s平面的映射关系二.z变换与拉式变换表达式之对应
2009-09-30 19:40:36 46
46 拉普拉斯变换视频教程免费下载:一 拉普拉斯变换的定义 1、从绝对可积条件讨论傅氏变换的问题,引入衰减因子的概念; 2、导出拉氏变换与逆变换公式; 3、单边拉氏变换的概念;
2009-09-03 12:00:40 226
226 连续时间LTI系统的复频域分析:连续时间LTI系统的复频域分析一、用拉普拉斯变换法求解微分方程 1.拉普拉斯变换法的优点 2.微分方程的拉氏变换二、基于s域模型的电路分析 1.电阻元
2009-09-03 11:59:58 18
18 拉普拉斯变换的基本定理
本节介绍拉普拉斯变换(也称为拉氏变换)的基本性质,了解掌握了这些性质,可以更加方便地求解各种拉普
2009-07-27 11:43:12 22114
22114 拉普拉斯变换教案:§13-1 拉普拉斯变换的定义§13-2 拉普拉斯变换的基本性质§13-3 拉普拉斯反变换的部分分式展开§13-4 运算电路§13-5 应用拉普拉斯变换法分析线性电路
2009-07-09 11:37:56 71
71 拉普拉斯变换及其应用:1.1基本要求1,熟悉拉氏变换的基本法则2,熟练掌握典型函数的拉氏变换式。3,掌握用拉氏变换求解微分方程初值问题的思路。4,熟练掌握求有理分式
2009-07-08 11:43:00 128
128 什么是拉普拉斯变换
拉普拉斯变换:拉普拉斯变换(英文:Laplace Transform),是工程数学中常用的一种积分变换。如果定义: f(t),是一个关于t,的函数,使得当t<0
2009-07-08 11:42:30 4963
4963 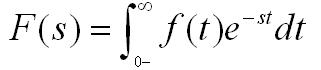
拉普拉斯变换公式
1、拉氏变换定义
2009-07-08 11:36:57 12239
12239 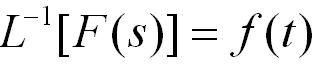
1、元件的复频域模型2、应用拉氏变换分析线性动态电路 R和C的复频域模型13-1 有关知识的复习13-2 应用拉氏变换分析电路
2009-07-08 10:33:21 67
67 介绍了一种变换近似方法,该方法通过变换近似获得重尾分布的拉普拉斯变换,解决了不存在拉普拉斯变换分布的信源排队等待时间分析问题,为实际网络排队缓冲器的设计提供
2009-02-28 16:33:18 20
20 动态电路的复频域分析 6.1 拉普拉斯变换及其性质 6.2 拉普拉斯反变换 6.3 电路基本定律及电路元件的复频域形式 6.4 应用拉普拉斯变换分
2008-12-04 17:55:29 40
40
![]() 的区间。这就相当于将函数乘上了单位阶跃函数,即:
的区间。这就相当于将函数乘上了单位阶跃函数,即:![]()
![]() 在区间
在区间![]() 内绝对可积,则它的傅里叶变换为:
内绝对可积,则它的傅里叶变换为: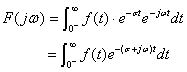 (式9-1-1)
(式9-1-1)![]() ,记为:
,记为:![]()
 电子发烧友App
电子发烧友App









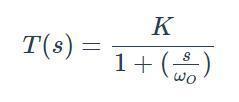





















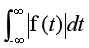






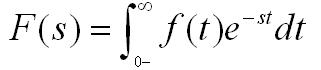










评论