由电磁感应定律可知,只要穿过线圈的磁力线(磁通)发生变化,则在线圈中就会感应出电动势。一个线圈由于其自身电流变化会引起交链线圈的磁通变化,从而在线圈中感应出自感电动势。如果电路中有两个非常靠近的线圈,当一个线圈中通过电流,此电流产生的磁力线不但穿过该线圈本身,同时也会有部分磁力线穿过邻近的另一个线圈。这样,当电流变化时,邻近线圈中的磁力线也随之发生变化,从而在线圈中产生感应电动势。这种由于一个线圈的电流变化,通过磁通耦合在另一线圈中产生感应电动势的现象称为互感现象。互感现象在工程实践中是非常广泛的。
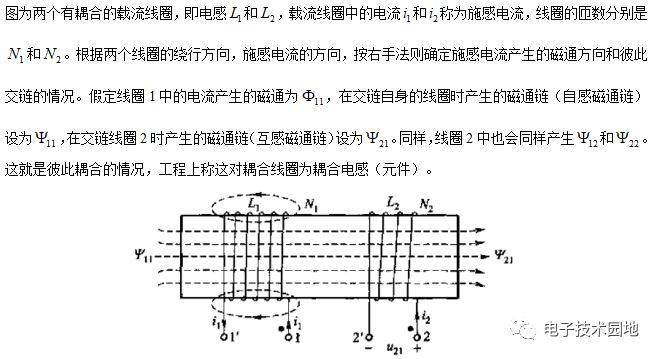
由4-2-1示出了两个位置靠近的线圈1和线圈2,它们的匝数分别为N1和N2。当线圈1通以电流i1时,在线圈1中产生磁通,其方向符合右手螺旋定则。线圈1的自感为
![]() 称为自感磁链。
称为自感磁链。
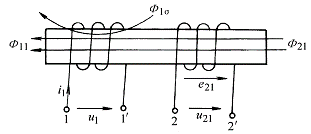
图4-2-1
由i1产生的部分磁通![]() 同时也穿越线圈2,称为线圈1对线圈2的互感磁通,此时线圈2中的互感磁链为
同时也穿越线圈2,称为线圈1对线圈2的互感磁通,此时线圈2中的互感磁链为![]() 。类似于自感磁链的情况,互感磁链与产生它的电流i1之间存在着对应关系。如果两个线圈附近不存在铁磁介质时,互感磁链与电流之间基本成正比关系。这种对应关系可用一个互感系数来描述,即有
。类似于自感磁链的情况,互感磁链与产生它的电流i1之间存在着对应关系。如果两个线圈附近不存在铁磁介质时,互感磁链与电流之间基本成正比关系。这种对应关系可用一个互感系数来描述,即有
(4-2-1)
互感系数简称为互感,其单位为亨利(H)。
下面分析两个线圈的实际绕向与互感电压之间的关系。本书前章已论述,对于线圈自感电压而言,只要规定线圈电流与电压参考方向一致,自感电压降总可以写为,与线圈的实际绕向无关。但对于二个线圈之间的互感而言,绕圈的绕向会影响互感电压的方向。因为产生于一个线圈的互感电压是由另一个线圈中的电流所产生的磁通变化引起的,要判断一个线圈中的电流变化在另一线圈中产生的感应电动势方向,首先要知道由电流产生的磁通的方向,而这一方向是与线圈绕向和线圈间的相对位置直接相关的。图4-2-2示出了绕在环形磁
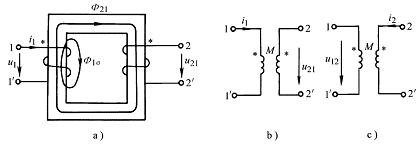
图4-2-2
路上的两个线圈的实际绕向。当电流i1从线圈1端流入时,它在线圈2中产生的磁通![]() 的方向如图4-2-2a所示。如果规定线圈2中互感电压u21的参考方向为从线圈2端指向端,使得电压u21的参考方向与
的方向如图4-2-2a所示。如果规定线圈2中互感电压u21的参考方向为从线圈2端指向端,使得电压u21的参考方向与![]() 符合右手螺旋法则,则由电磁感应定律可知,此时电压u21的表达式为:
符合右手螺旋法则,则由电磁感应定律可知,此时电压u21的表达式为:
即是说,图4-2-2所示的绕向结构,当规定电流i1的方向从1端流向 端,电压u21的参考方向从2端指向端,由i1产生的互感电压
端,电压u21的参考方向从2端指向端,由i1产生的互感电压![]() 取正号。
取正号。
在实际电路中,互感元件通常并不画出绕向结构,这样就要用一种标记来指出两个线圈之间的绕向结构关系。电工理论中采用一种称为同名端的标记方法,用*号来特定标记每个磁耦合线圈的一个对应端钮。同名端标记的方法为:先在第一个线圈的任一端作一个标记,令电流i1流入该端口;然后在另一线圈找出一个端点作标记,使得当i2电流流入该端点时, i1与i2两个电流产生的磁通是互相加强的,称这两个标记端为同名端。图4-2-2中的耦合线圈的同名端可由上述法则判断,线圈1端与线圈2端为同名端。当然 与也为同名端。
与也为同名端。
标出了两个线圈的同名端后,我们就可以把图4-2-2a所示结构的耦合线圈用图4-2-2b的互感耦合线圈符号图来表示,而不必画出线圈之间的绕向。
图4-2-3表示与上面不同绕向的互感耦合线圈,根据上面所述的同名端的标识方法可知,线圈1端与端为同名端。线圈的符号如图4-2-3所示。
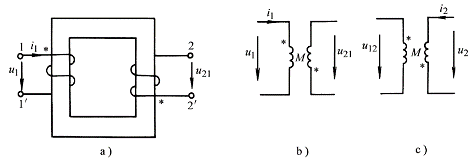
图4-2-3
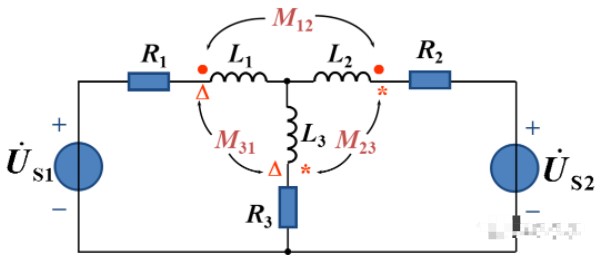
两个以上的线圈互相之间存在电磁耦合时,各对线圈之间的同名端应用不同的符号加以区别。对于图4-2-4所示电路来说,线圈1与2之间的同名端用*号表示,线圈2与3之间的同名端用○号表示,线圈1与3之间的同名端用△号表示。
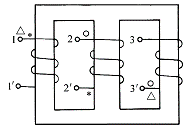
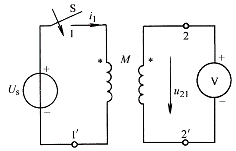
图4-2-4 图4-2-5
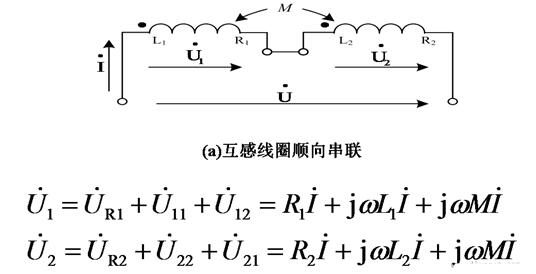
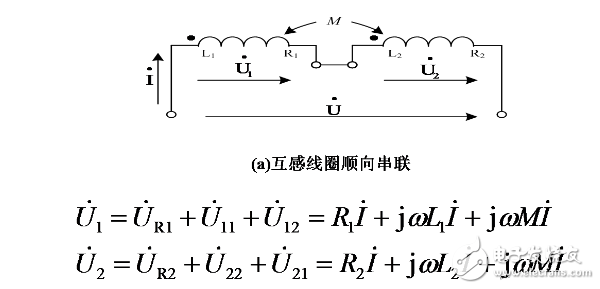
下面讨论具有互感的支路电压与电流的一般形式。设有两个互感耦合线圈,线圈1自感为L1,电阻为R1,线圈2自感为L2,电阻为R2,两线圈互感系数为M。现将两线圈按图4-2-6a

图4-2-6
所示顺向串接,在端口加正弦交流电压 ,则可写出线圈1中电压为:
,则可写出线圈1中电压为:
![]()
线圈2中电压为:
![]()
总电压为:
![]()
相量图如图4-2-6b所示。电路总等值阻抗为:
![]() (4-2-4)
(4-2-4)
可见在这种连接方式下等值电感![]() ,其值大于两线圈自感之和,这是因为两线圈产生的磁通互相加强。
,其值大于两线圈自感之和,这是因为两线圈产生的磁通互相加强。
如果将上述具有互感耦合的线圈并联连接,且把同名端连在一起,如图4-2-8a所示,当外加电压为正弦电压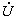 时,可写出方程:
时,可写出方程:
![]()
![]()
联立求解上两个方程,得:
![]()
图4-2-8
总电流为:
![]()
等效入端阻抗为:
![]() (4-2-6)
(4-2-6)
同理可推出当异名端连在一起时,如图4-2-8b所示电路,入端阻抗为:
![]() (4-2-7)
(4-2-7)
 电子发烧友App
电子发烧友App
























评论