本节主要是对通用无源电路网络的原理图构建和电路仿真。主要介绍了电路方程的改进节点法和原理图构建中所使用的图论相关分析方法。最后结合实际滤波器电路,使用Matlab实现了一个通用无源网络仿真引擎,附Github链接。
通用无源网络仿真(AC和瞬态)
interwetten与威廉的赔率体系 无源滤波器设计(三)-通用梯形电路网络分析和仿真中所介绍的电路网络分析只是针对梯形无源网络,由于使用了网孔分析的方法,所以还存在诸多缺陷:
对于为0的电容,其阻抗为无穷大,网孔方程将无法列解
由于滤波器设计非常关注其瞬态响应,之前的方程将不能满足瞬态响应的数值求解
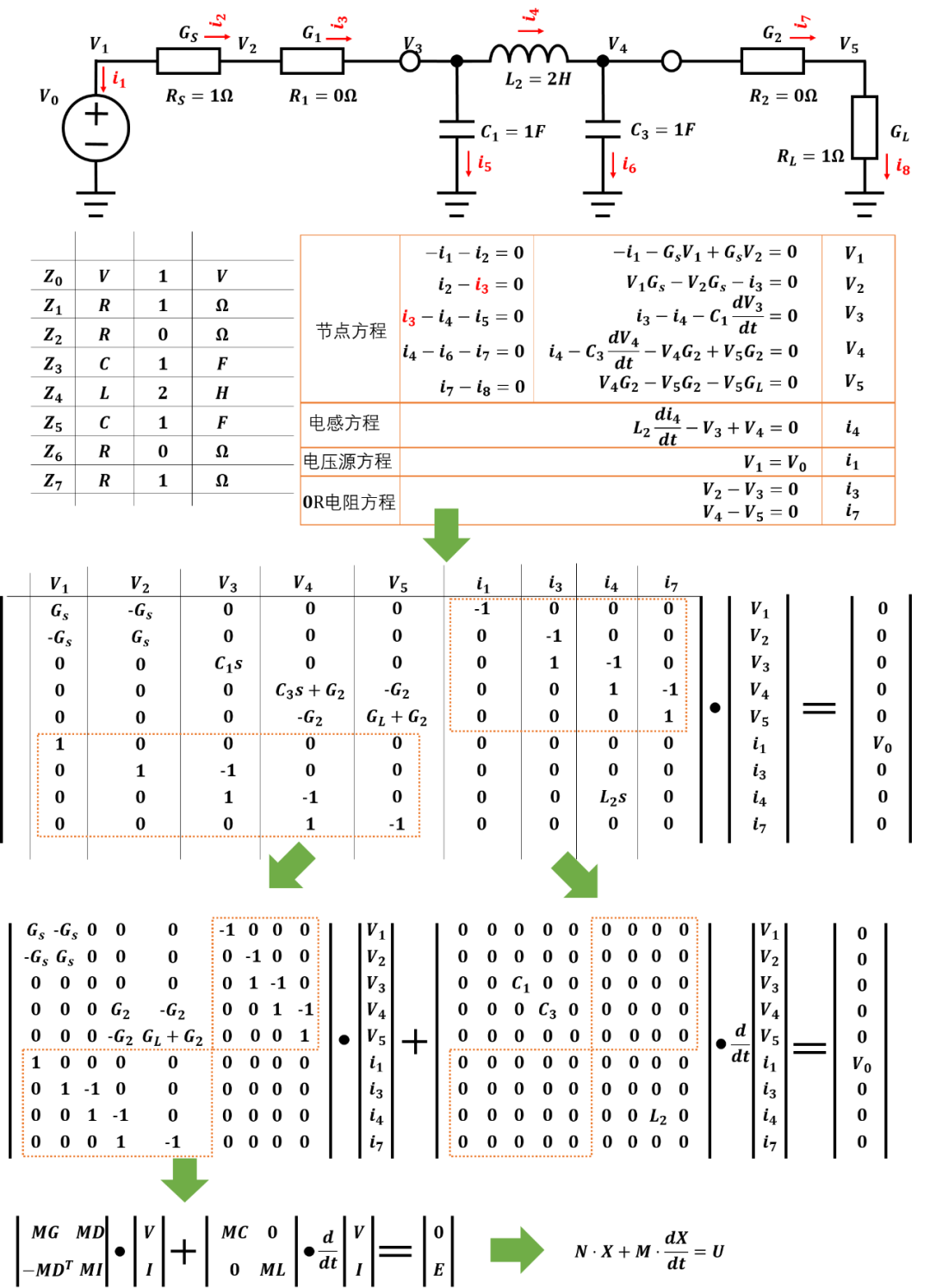
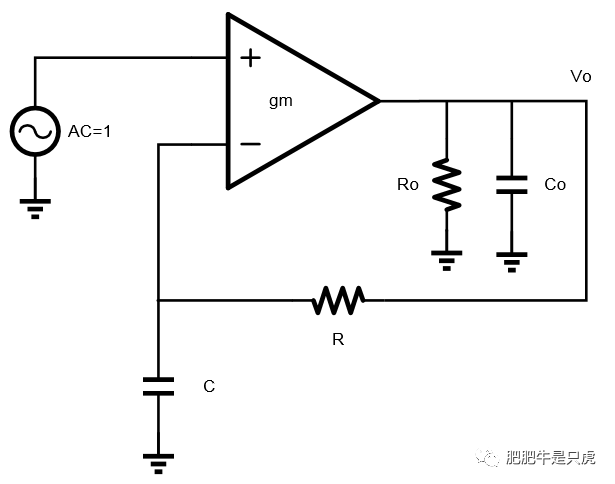
基于以上两点,电路方程将使用改进的节点方程形式(The modified node equation): 这种方程形式将电路方程分解为两部分,一部分是微分电路矩阵 ,一部分是常数电路矩阵 ,这种形式方程可以非常容易进行数值分析和处理。 式中M矩阵中包含电路中所有的微分电路器件,如电感的电压就是其电流的微分形式 ,电容的电流是其电压的微分形式 .而N中包含电路的电阻和电导器件,如电阻 。 方程构建过程如下图所示:
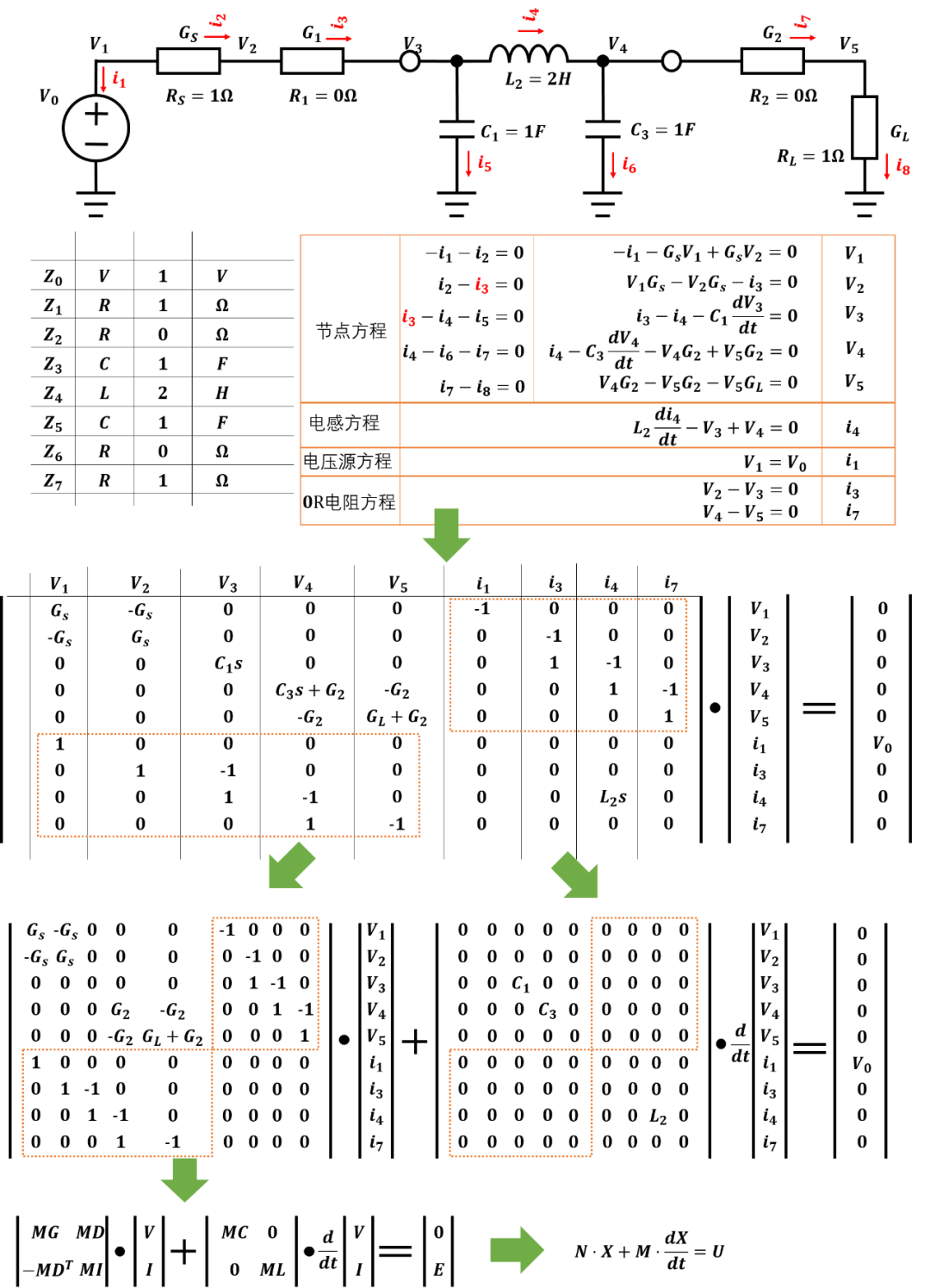
矩阵构建规则是:
当电阻 连接在vs和ve节点之间时,需要在 矩阵的(vs,vs)和(ve,ve)位置增加 ,在N矩阵的(vs,ve)和(ve,vs)位置增加 。
当电阻 连接在vs和GND节点之间时,只需要在 矩阵的(vs,vs)位置增加 即可。
构建电流源支路的关联矩阵 ,设电流i所连接的节点是vs和ve时,规定电流vs到ve电流为正方向,那么在N矩阵中i所对应节点vs设置为1,在ve节点设置为-1。
当电路中存在电压源时,定义电压源电流 ,关联矩阵的 位置为1或-1,并且将E矩阵的 位置写电压源值。
当电路中存在电流源时,定义电流源电流 ,在 矩阵的 位置写1,并且将 矩阵 位置写入电流源电流值。
矩阵构建规则是:
当电容 连接在vs和ve节点之间时,需要在 矩阵的(vs,vs)和(ve,ve)位置增加 ,在 矩阵(vs,ve)和(ve,vs)位置增加 。
当电容 连接在vs和 节点之间时,只需要在 矩阵的(vs,vs)位置增加 即可。
当电感 的电流定义为i时,则需要在 矩阵的(i,i)位置设置为 。
矩阵 和 构造完成后,可以用后向欧拉法(Backward Euler method, BE)解微分方程求得瞬态特性。 式中 是步进,所以 : 用此公式可以计算出瞬态值 ,下图就是之前的3阶数巴特沃斯滤波器的瞬态响应曲线。
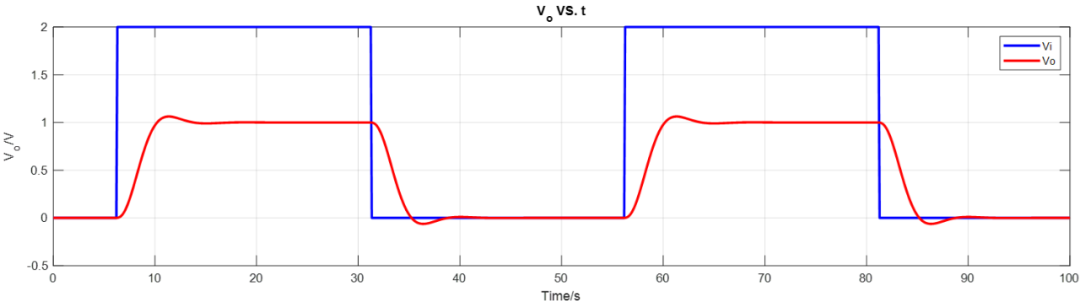
使用公式可以计算AC特性 下图就是之前的3阶数巴特沃斯滤波器的AC频率响应曲线。
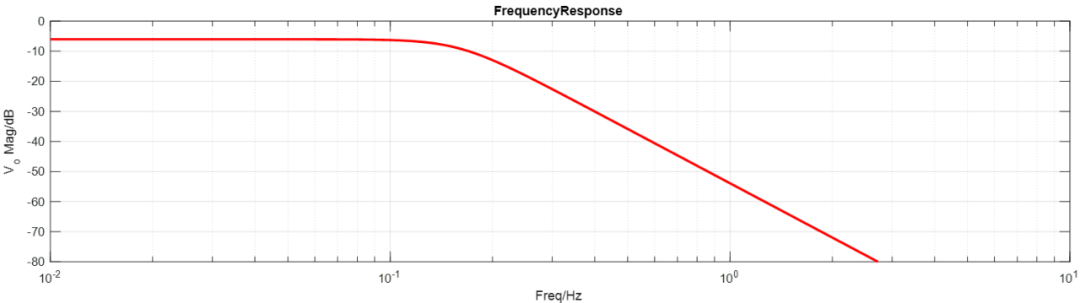
无源电路网络原理图构建
无源电路网络原理图构建可以将抽象的网表文件转换为形象的原理图,便于分析和理解。原理图的构建本质上是一个图论问题,如何在平面内将图的枝节有意义的展示出来。这里分别讨论了两种不同的原理图生成策略: 策略一 使用最长路径构建原理图(这里采用图论算法中的深度搜索(图的存储,董晓算法)+回溯算法实现,实际上是解一个NP完全问题,有兴趣的可以搜索哈密顿回路问题,Hamiltonian path problem 一道题难倒百万人?一笔画问题与哈密顿问题该怎么解?)。 本例子使用了比较复杂的例子用以比较不同策略的计算结果。
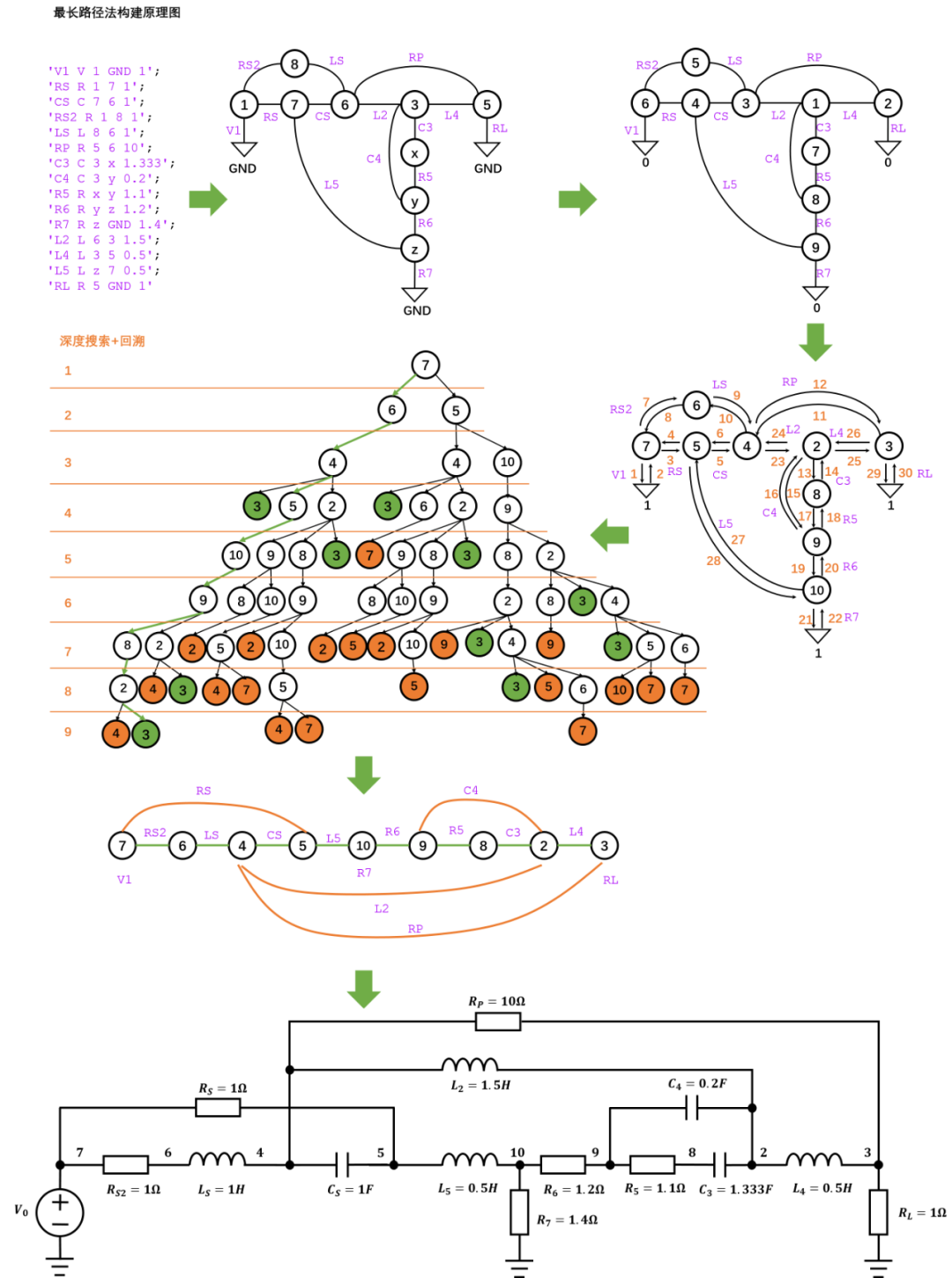
策略二 使用给定频率点 的最小阻抗路径构建原理图(这里使用Dijkstra求最小路径算法实现)。
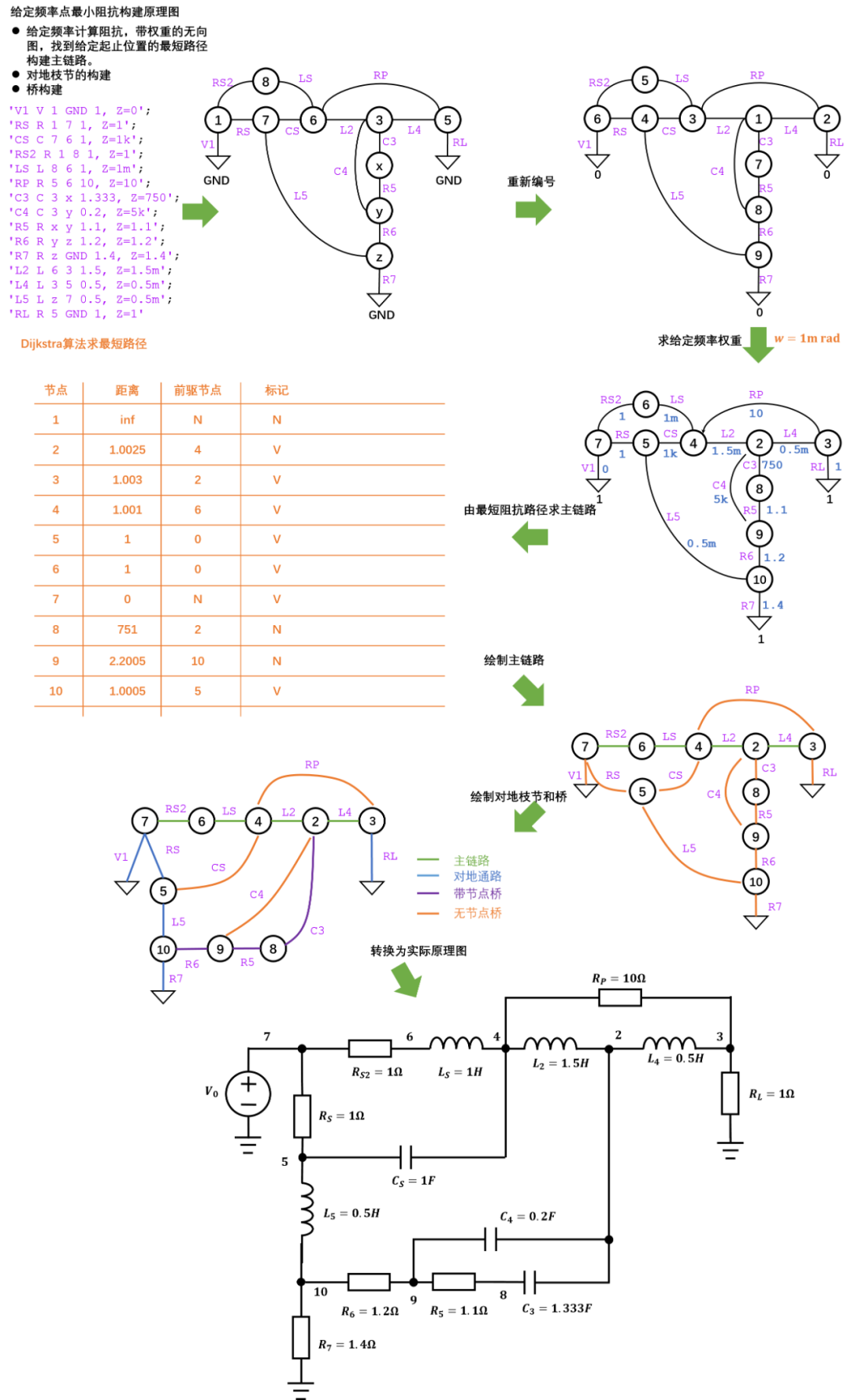
最终效果可以看出策略二所构建出来的原理图比较容易读懂,后续电路设计软件中将采用第二种方法生成原理图,对于滤波器设计,所有给定的原理图构建频率 需要在其通带范围内。 原理图构建采用前述策略二:
由给定 求出从源到负载的最短路径(MainPath)
由MainPath各个节点出发到 的路径(Branch2GNDPath)
由前两种路径节点(或桥)为起点和终点所构成的包含节点的桥(WiNodeBridge)
剩下的则为无节点桥(WoNodeBridge)
通过以上策略即可完成构建整个原理图
无源电路网络仿真引擎
无源电路网络仿真引擎采用Matlab编程,主要分为3大模块:
原理图构建模块
AC仿真模块
瞬态仿真模块
5阶椭圆低通滤波器仿真
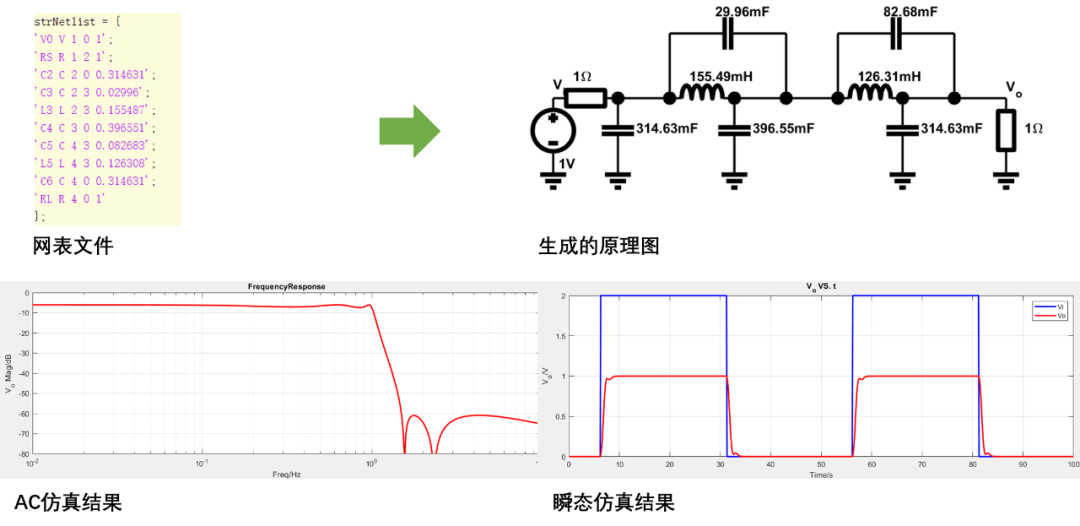
5阶巴特沃斯带通滤波器仿真(设计的滤波器中心频率为1Hz,瞬态给定的是频率为1Hz的方波信号。PS:瞬态仿真中步进需要取小些)
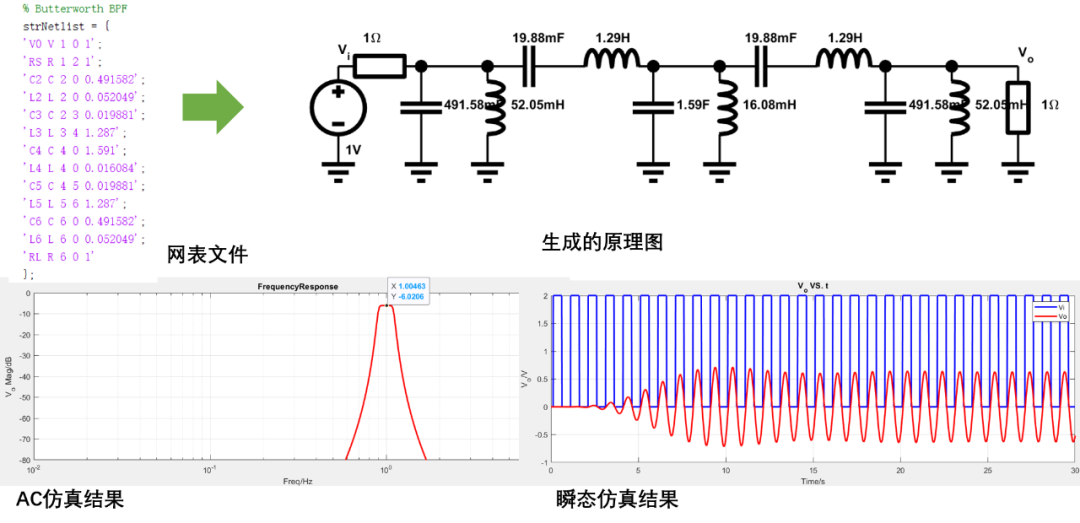
使用Spectre仿真器对上述带通滤波器进行仿真
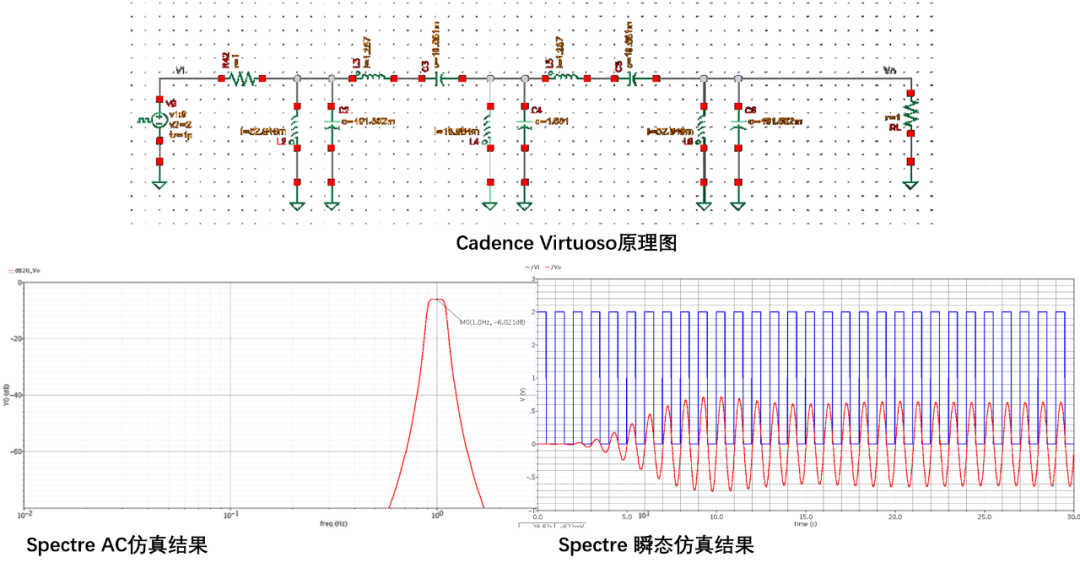
仿真结果对比:
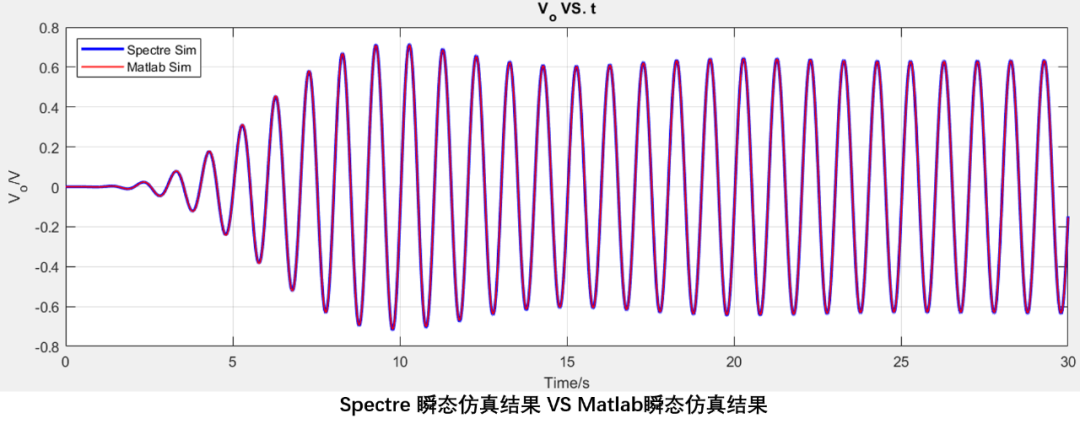
从图中可以看到,Matlab仿真结果和Spectre仿真结果基本一致。 源码见 : https://github.com/etools361/LadderNetworkSimEngine.git
审核编辑 :李倩
 电子发烧友App
电子发烧友App












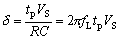











评论