|
6.3.1 超前校正
用频率法对系统进行超前校正的基本原理是:通过所加的校正装置的相位超前特性来增大系统的相位裕量,改变系统开环频率特性,并要求校正网络最大的相位超前角
φm出现在系统新的剪切频率处,使校正后系统具有如下特点:低频段的增益满足稳态精度的要求;中频段对数幅频特性的斜率为-20db/dec ,并具有较宽的频带,使系统具有满意的动态性能;高频段要求幅值迅速衰减,以减少噪声的影响。
用频率法对系统进行串联超前校正的一般步骤可分为:
1)根据稳态误差的要求,确定系统的开环增益K,并据此画出未校正系统的伯德图,并测出其相位裕量γ1。
2)由期望的相位裕量值γ ,计算超前校正装置应提供的相位超前量 φ,即
式中的ε是用于补偿因超前校正装置的引入,使系统的剪切频率增大而导致未校正系统相角迟后量的增加。ε值可以这样估计的:如果未校正系统的开环对数幅频特性在剪切频率处的斜率为-40db/dec ,一般取ε=5°-10° ;如果该频段的斜率为
-60db/dec ,则取ε=15°-20°。
3)根据所确定的最大相位超前角φm ,按式(6—8)算出相应的 α值,即
4)计算校正装置在ωm处的幅值10lg1/α (参见图6—5)。由未校正系统的对数幅频特性图,求得其幅值为-10lg1/α 处的频率,则该频率ωm就是校正后系统的开环剪切频率ωm,即ωc=ωm 。
5)确定校正网络的转折频率ω1 和ω2
| |
 |
, |
6)画出校正后系统的伯德图,并验算相位裕量是否满足要求?如果不满足,则需增大ε值,从步骤3)开始重新进行计算,直到满足要求。
例 6—1 设一单位反馈系统的开环传递函数为:
设计一超前校正装置,使校正后系统的静态速度误差系数 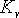 等于 等于  ,相位裕量γ不小于 ,相位裕量γ不小于  ,增益裕量 ,增益裕量  不小于 不小于  . .
解:(1)根据对静态速度误差系数的要求,确定系统的开环增益K。
 , , 
当 时,未校正系统的开环频率特性为 时,未校正系统的开环频率特性为

绘制未校正系统的伯德图,如图6—6中的虚线所示。由该图或用Matlab中的margin命令,可得未校正系统的幅值裕量为无穷大,相位裕量约为 。 。
(2)根据相位裕量的要求确定超前校正网络的相位超前角:

(3)由式(6—8)求得:
(4)超前校正装置在 处的幅值为: 处的幅值为: 
 ,在未校正系统的开环对数幅值对应的频率 ,这一频率即为校正后系统的剪切频率 ,在未校正系统的开环对数幅值对应的频率 ,这一频率即为校正后系统的剪切频率  。 。
(5)确定超前校正网络的转折频率 ,并确定超前装置的传递函数。 ,并确定超前装置的传递函数。
由  ,则 ,则  , ,  
,于是求得超前校正网络的传递函数为

为补偿因超前校正网络的引入而造成系统开环增益的衰减,必须使附加放大器的放大倍数为 .
(6)校正后系统的开环传递函数为:

对应的伯德图如图6—15中的细实线所示。由该图可见,校正后系统的相位裕量γ为  ,增益裕量为 ,增益裕量为  ,,满足设计的要求。 ,,满足设计的要求。
通过上例可以看出,串联超前校正有如下特点;
1)这种校正主要对未校正系统中频段的频率特性进行校正,使校正后中频段幅值的斜率为-20db/dec,且有足够大的相位裕量。
2)超前校正会使系统瞬态响应的速度变快。由例6—1可知,校正后系统的剪切频率由未校正前的6.3增大到9。这表示校正后系统的频带变宽,瞬态响应的速度变快;但系统抗高频噪声的能力也变差。
3)虽然超前校正一般能较有效地改善系统的动态性能,但当未校正系统的相频特性曲线在剪切频率ωc附近急剧地下降时,若用单级的超前校正网络去校正,收效不大。因为校正后系统的剪切频率向高频段移动。在新的剪切频率处,由于未校正系统的相角迟后量过大,因而用单级的超前校正网络难于获得较大的相位裕量。此时可采用多级串联校正。
6.3.2 迟后校正
根据迟后校正网络具有低通滤波器的特性,因而当它与系统的不可变部分Gc(s)串联时,它对频率特性的低频段影响甚微,但会使系统开环频率特性的中频和高频段增益降低,剪切频率ωc减小,从而有可能使系统获得足够大的相位裕量。由此可见,迟后校正在一定的条件下,也能使系统同时满足动态和静态性能的要求。
不难看出,迟后校正的不足之处是:校正后系统的剪切频率ωc会减小,频带变窄,瞬态响应速度变慢;同时,在剪切频率ωc处,迟后校正网络会产生一定的相角迟后量。为此,应尽可能地减少迟后角。理论上可选取 的两个转折频率ω1 、ω2比
ωc越小越好,但考虑到物理实现上的可行性,一般取ω2=1/T=ωc/5 ~ωc/10为宜。
根据上述分析,用频率法对系统进行迟后校正的一般步骤为:
1)根据给定静态误差系数的要求,计算系统的开环增益K。并画出未校正系统的伯德图,求出相应的相位裕量和增益裕量。
2)在已作出的相频曲线上寻找一个频率点,要求在该点处的开环频率特性的相角为:φ=-180°+γ+ε
以这一频率作为校正后系统的剪切频率ωc 。上式中,γ为系统所要求的相位裕量,ε是补偿因迟后网络的引入而在剪切频率ωc处产生的相位迟后量,工程上可取
ε=5°-10°。
3)设未校正系统在处ωc的幅值等于20lgβ,据此确定迟后网络的β值。据此可保证在剪切频率ωc处,校正后开环系统的幅值为0。
4)选择迟后校正网络中的一个转折频率ω2=1/T=ωc/5 ~ωc/10,则另一个转折频率为ω1=1/βT 。
5)画出校正后系统的伯德图,并求出校正后系统的相位裕量。校核设计指标,如果不满足要求,则可通过改变T值,重新设计迟后校正网络。
例6—2 设一单位反馈系统的开环传递函数为
要求设计一串联迟后校正装置,使系统具有下列的性能指标:静态速度误差系数 ;相位裕量γ不低于 ;相位裕量γ不低于 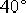 ;增益裕量不小于10dB。 ;增益裕量不小于10dB。
解:(1)调整开环增益K,使之满足静态速度误差系数的要求。

增益调整后系统的开环频率特性为:

相应的伯德图如图6—16中的虚线所示。由该图可知,未校正系统的相位裕量约等于 ,或使用Matlab中的margin函数,可得到校正前的系统是不稳定的。 ,或使用Matlab中的margin函数,可得到校正前的系统是不稳定的。
(2)在作出的相频特性曲线上,根据下式确定相角

对应于这个φ角的频率 ,并选它作为校正后系统的剪切频率 ,并选它作为校正后系统的剪切频率 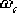 。 。
(3)计算 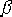 。由于未校正系统在 。由于未校正系统在  处的幅值等于20dB,即 处的幅值等于20dB,即  ,故β=10。 ,故β=10。
(4)取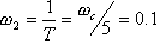 ,则 ,则  。这样,迟后校正网络的传递函数为: 。这样,迟后校正网络的传递函数为: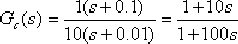
(5)校正后系统的开环传递函数为

对应的伯德图如图6—16中的实线所示。由图或由Matlab中的margin函数可知,校正后系统的相位裕量约为 ,增益裕量约等于14dB,满足设计要求。 ,增益裕量约等于14dB,满足设计要求。
6.3.3 迟后-超前校正
如果未校正系统为不稳定,或对校正后系统的动态和静态性能均有较高的要求时,只采用上述的超前校正或迟后校正,难于达到预期的校正效果。此时,宜对系统采用串联迟后—超前校正。
应用频率法设计迟后-超前校正装置,即利用校正装置的超前部分来增大系统的相位裕量,以改善其动态性能,但因加大了带宽,易受高频噪声的影响,降低了系统的抗干扰能力;利用它的迟后部分来改善系统的静态性能,但会恶化系统的动态性能,对系统的相对稳定性不利。因此采用这种校正方式,应合理应用迟后和超前校正各自的优点,克服它们各自的弱点,经多次试探才能成功。
例6—3 设一单位反馈系统的开环传递函数为:

要求校正后系统具有下列的性能指标:相位裕量 ;增益裕量 ;增益裕量  ;静态速度误差系数 ;静态速度误差系数  。。试设计一迟后—超前校正装置。 。。试设计一迟后—超前校正装置。
解:与超前校正和迟后校正相似,迟后—超前校正可按如下步骤进行:
(1)求取开环增益并作出伯德图。其根据对 的要求,系统的增益K由 的要求,系统的增益K由
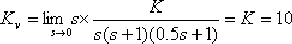
求得K=10。
未校正系统的伯德图如图6—17中的虚线所示。由图可得到系统相位裕量等于 ,表明原系统是不稳定的。在这种情况下,如果采用超前校正,由于系统的剪切频率的增大使原系统产生的迟后相位的增加比超前校正装置提供的相位增加还快,这样无法起到校正的作用,同时将增大剪切频率,不利抑制噪声。
(2)确定校正后系统的剪切频率 。在未对系统的快速性提出要求时,可选择相频特性上相角等于 。在未对系统的快速性提出要求时,可选择相频特性上相角等于  的频率作为校正后系统的剪切频率 的频率作为校正后系统的剪切频率  。在本题中,由未校正系统的相频曲线可见,当 。在本题中,由未校正系统的相频曲线可见,当  时, 时,  。选择该频率值作为校正后系统的剪切频率 。选择该频率值作为校正后系统的剪切频率  ,显然较为合理。因为迟后—超前校正网络在该频率处产生 ,显然较为合理。因为迟后—超前校正网络在该频率处产生  的相位超前角是完全能实现的,并且 的相位超前角是完全能实现的,并且  也不算小,使校正后的系统仍具有一定的响应速度。 也不算小,使校正后的系统仍具有一定的响应速度。
(3)确定迟后—超前网络的转折频率。首先确定迟后部分的转折频率,令它的一个转折频率  ,选取β=10,则另一个转折频率 ,选取β=10,则另一个转折频率  ,于是求得校正装置迟后部分的传递函数为 ,于是求得校正装置迟后部分的传递函数为

它在剪切频率  处产生约 处产生约  的相位迟后。接着确定超前部分的转折频率:由图6—29可见,未校正系统在 的相位迟后。接着确定超前部分的转折频率:由图6—29可见,未校正系统在  处的幅值为13dB,欲使该频率成为校正后系统的剪切频率,必须使该频率点的开环幅值为0dB,即要求迟后—超前网络在 处的幅值为13dB,欲使该频率成为校正后系统的剪切频率,必须使该频率点的开环幅值为0dB,即要求迟后—超前网络在  处产生-13dB的幅值。据此,通过点 处产生-13dB的幅值。据此,通过点  , 作一条斜率为 , 作一条斜率为  的直线,该直线与0dB线与-20dB的水平线的交点,它们分别为 的直线,该直线与0dB线与-20dB的水平线的交点,它们分别为  , ,  ,就是要求的超前部分的转折频率。因此超 ,就是要求的超前部分的转折频率。因此超
前部分的传递函数为: 
将校正网络的迟后部分和超前部分的传递函数组合在一起,就得到迟后—超前校正网络的传递函数:

(4)校正后系统的开环传递函数为:

相应的伯德图如图6—17中的实线所示。校正后系统的相位裕量 ,增益裕量13.6db,静态速度误差系数 ,增益裕量13.6db,静态速度误差系数  ,所要求的性能指标均已满足。 ,所要求的性能指标均已满足。
前面我们介绍了基于频率法的串联控制器的顺向设计方法,即依据指标或设计要求,首先选择三类控制器中的一种方式,然后按设计规则进行设计。事实上,若能根据指标设计出校正后的期望频率特性,则根据:G(jω)=Gc(jω)G0(jω) ,由校正前后的幅频特性和相频,亦可得到待定的控制器。此法对于最小相位系统尤其有效。
6.3.4基于频率法的Matlab串联校正设计
根据上面对三类控制器频率法设计思路的介绍,可总结出一般性的设计步骤:
(1)根据静态性能指标,设计开环系统的增益,然后求出校正前系统的幅值裕量和相位裕量,并与设计要求比较;
(2)确定校正后期望的剪切频率ωc,具体值的选取与选择的校正方式(相位超前、迟后或迟后-超前等)相适应;
(3)根据待设计的校正装置的形式和转折频率,计算有关参数,进而确定校正装置;
(4)得出校正后系统,并校验是否满足设计要求。不满足,则从(2)重新开始。
但毕竟,控制系统的设计是一项十分麻烦的工作,并需要大量的经验,为此,可借助飞速发展的计算机仿真威廉希尔官方网站
,简化控制系统的设计工作。
本节介绍频率法的MATLAB设计方法,主要利用伯德(Bode)图进行系统的设计,常用的函数有:
Bode--—伯德图作图命令;
Margin—求取系统的幅值裕度和相位裕度;
Bode_asymp—伯德图幅频特性的渐近线(自编函数);
Semilogx—半对数作图函数;
Logspace—用于在某个区域中产生若干频点;
Nicols、Mgrid—用于Nicols曲线和等M圆、等N圆的作图命令;
Nyquist—Nyquist曲线作图命令;
Phase、Abs—求取复数行矢量的相角和幅值函数。 这些函数或命令大部分在第五章或第九章作过说明。
结合例6-4介绍采用Matlab进行设计的具体步骤,设计一个补偿器
例6-4 对一给定的对象环节:
设计一个补偿器,使校正后系统的静态速度误差系数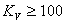 ,剪切频率大于60,相位裕量 ,剪切频率大于60,相位裕量  。 。
解:(1)首先根据对静态速度误差系数的要求,确定系统的开环增益K=100。
(2)写出系统传递函数G0并计算其幅值裕量和相位裕量:
G0=tf(100,conv([1,0],[0.04,1]));
[Gm,Pm,Wcg,Wcp]=margin(G0);[Gm,Pm,Wcg,Wcp]
ans =
Inf 28.0202 NaN 46.9782
w=logspace(-1,3);[m,p]=bode(G0,w);
subplot(211),semilogx(w,20*log10(m(:)))
subplot(212),semilogx(w,p(:))
可以看到,未校正环节的幅值裕量无穷大,相位裕量 ,剪切频率 ,剪切频率  ,不满足要求。其伯德图如图6-18a中的虚线所示。 ,不满足要求。其伯德图如图6-18a中的虚线所示。
(3) 根据系统对动态性能的要求,可试探性引入一个超前补偿器来增加相角裕量,则可假设校正装置的传递函数为:
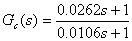
则可通过下列的Matlab语句得到校正后系统的幅值裕量和相位裕量:
Gc=tf([0.0262,1],[0.0106,1]);bode(Gc,w)
G_o=Gc*G0;[Gm,Pm,Wcg,Wcp]=margin(G_o);[Gm,Pm,Wcg,Wcp]
ans =
Inf 47.5917 NaN 60.3252
从而可得到补偿器的Bode图如图6-18b所示。可以看出,在频率  处系统的幅值和相位均增加了。在这样的控制器下,校正后系统的相位裕量增加到 处系统的幅值和相位均增加了。在这样的控制器下,校正后系统的相位裕量增加到  ,而剪切频率增加到 ,而剪切频率增加到  。 。
(4) 绘制校正后系统的Bode图如图6-18a中的实线所示。用如下的Matlab语句绘制校正前后系统的阶跃响应曲线如图6-18c。
[m,p]=bode(G0,w);[m1,p1]=bode(G_o,w);
subplot(211),semilogx(w,20*log10([m(:),m1(:)]))
subplot(212),semilogx(w,[p(:),p1(:)])
G_c1=feedback(G0,1);G_c2=feedback(G_o,1);
[y,t]=step(G_c1);y=[y,step(G_c2,t)];
figure,plot(t,y)
|  电子发烧友App
电子发烧友App

 硬声App
硬声App

 1827
1827 884
884 2258
2258 2593
2593 840
840 2767
2767
 2788
2788 6
6 4
4 603
603 2
2 10
10 9066
9066 87525
87525 55
55 1
1 51
51 60
60 305
305 53
53
 69
69 1984
1984
 359
359 837
837
 1741
1741
评论