Abstract: Controlling fan speed as a function of temperature is a useful technique for reducing system noise and increasing the fan's lifetime. Two different types of integrated circuits (ICs) that can be used to control fan speed are discussed.
Brushless DC fan motors can be controlled using a variety of methods. The simplest method is on/off switching with a single transistor. Digitally programmable variable control can be achieved using linear regulators or power op amps combined with DACs or using PC health monitor ICs which offer DACs with an output that can be applied to an amplifier for driving a fan. PWM fan control chips are available that require a DAC for digital interface. Note that PWM methods have to be used with some caution.
The newest developments for fan control are digital interface ICs with complete fan driver circuits, such as the MAX1669, which include everything except for the power transistor. The MAX6650/MAX6651 take the forefront in advanced fan control because these devices are truly fan speed regulators.
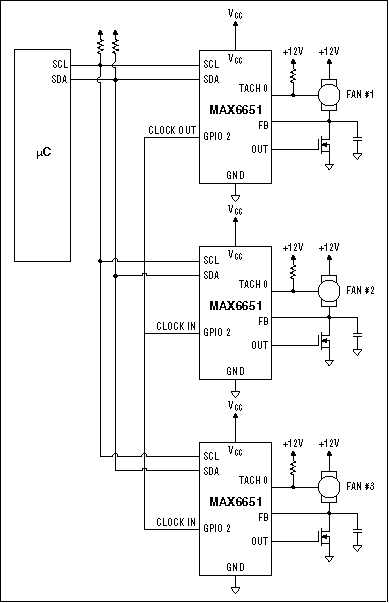
The MAX1669 represents the most common type of fan control available, providing either a linear DAC output or a PWM output. It stands out because it includes a remote-junction temperature sensor input that can be connected to ICs equipped with sensing junctions or to bipolar transistors, such as 2N3904s, used as remote sensors. The MAX1669 is especially suited in situations where the fan cannot be equipped with a tachometer output because of either cost or technical requirements. Figure 1 is an example of the MAX1669 used for linear control of a fan.
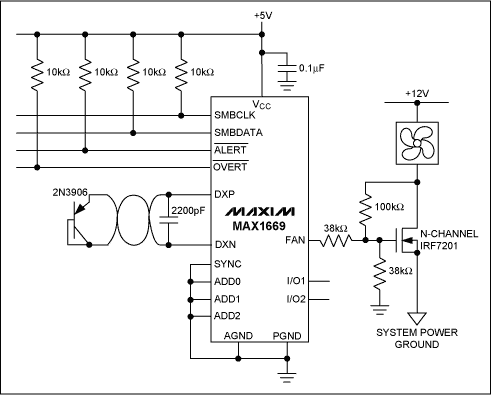
Figure 1. Typical circuit for linear control of a fan using the MAX1669.
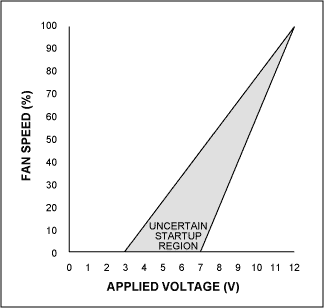
Figure 2. This graph depicts typical fan speed vs. applied voltage.
This lack of predictability of threshold voltages has given birth to some "Rube Goldberg" schemes among some of the fan control ICs. For instance, one IC examines whether or not the fan is rotating, and if it isn't, it raises the drive incrementally. If the fan still isn't rotating it raises it another increment and so on until the fan starts.
The MAX1669, along with a tachometer feedback amplifier, offers a "clean" solution to this problem by regulating fan speed (Figure 3). This trades complexity along with the effort of designing the fan control amplifier. The feedback loop of the fan control amplifier contains both differentiation and integration, the time constants of which have to be found empirically for a given make and model of fan (once found, they can be fixed for production). This additional circuit adds cost in with its higher component count.
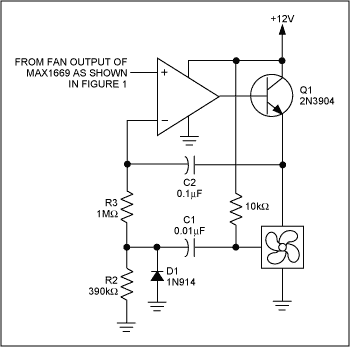
Figure 3. Using this fan control amplifier with the MAX1669 will provide full range linear regulation (as opposed to fan control) of fans equipped with tachometer outputs.
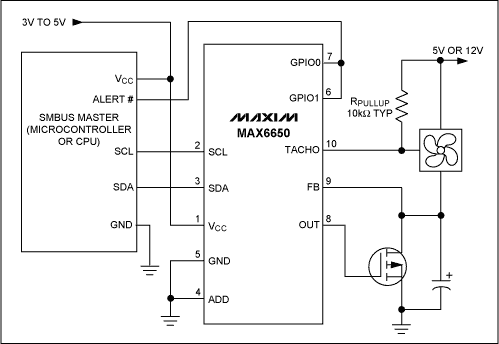
Figure 4. The MAX6650 is a true fan speed regulator, by virtue of including a tachometer output fan in its feedback loop.
Figure 4 depicts a typical application for the MAX6650. The MAX6650 regulates fan speed based on a code programmed into its fan speed register, by forcing the fan tachometer period to be equal to the scaled register value. Because typical fans produce two tachometer pulses per revolution, the required fan speed register value is calculated as:
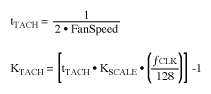
where:
KTACH = Value programmed into the fan speed register
tTACH = Period of the tachometer signal
KSCALE = Prescalar value (set in configuration register of the MAX6650/MAX6651 from 1 to 16 with a default of 4)
fCLK = MAX6650/MAX6651 clock frequency (254kHz typ)
The MAX6650/MAX6651 free the designer from the complex issues associated with closed-loop amplifier design, leaving only selection and installation of the pass transistor.
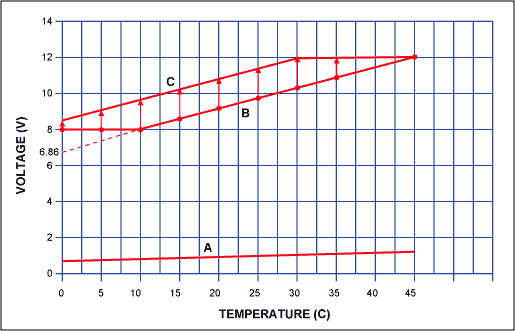
A resistive load, linear, control pass element will be subject to maximum dissipation when delivering half the total supply voltage across the load. But does a resistive load represent a good model for fans? The graph in Figure 4 answers this question and shows that modeling the fan as a resistive load would be more demanding than the actual real-world fan behavior would indicate. This suggests that conservative design practice can treat the fan as a resistive load with the only consequence being a choice of a larger pass transistor than might be used with careful fan characterization.
Figure 4 shows that as supply voltage increases, the fan current is nonlinear and always below the current equivalent to what a resistor would draw (sized according to full fan voltage and current). For instance, the Papst fan drew approximately 240mA at 12V. An equivalent resistance would consume 120mA at the half-voltage output point and correspond to a dissipation of 0.72W:

where PD represents worst-case resistive load dissipation.
Note from the graph of Figure 4 that the real-world Papst motor showed a true dissipation of 0.65W on the pass element. Even more revealing is the current behavior of the Superred fan, which steps down to a very low level at around 6V. A conservative design that considers the fan a resistive load would have quite a bit of safety margin with the Superred fan.
Once a given pass transistor has been selected, if the following equation is satisfied then no additional heatsinking is necessary:

where:
TJMAX = Maximum allowable junction temperature from transistor manufacturer's data sheet.
TA = Maximum expected ambient temperature.
PD = Power dissipation (same as Equation 3 above).
θJ-A = Thermal resistance, junction to ambient, from transistor manufacturer's data sheet.
If the equation is not satisfied, a heatsink must be selected to satisfy the following:
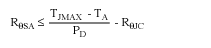
where:
RθSA = Heatsink thermal resistance (from heatsink manufacturer's data sheet).
RθJC = Pass transistor junction-to-case thermal resistance (from pass transistor manufacturer's data sheet).
The possibility of a total short circuit across the fan has not been discussed. If this happens, then the full current available from the fan power supply will flow through the pass transistor. If this condition is a consideration, then that current and voltage value should be used in all the power dissipation and heatsinking calculations. Alternatively, current limiting circuitry could be included on the pass transistor, such as the circuit shown in Figure 5. Calculate the value of the current limit resistor according t

where ILIMIT is the desired value of current limit. Note that this current limit circuit is temperature sensitive. The 0.6 term in the equation is actually the base-emitter voltage of the current limit transistor which varies according to -2.2mV/°C. This can be useful in that it acts to reduce the current limit as temperature rises.
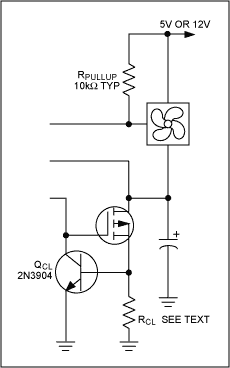
Figure 5. When current limiting is necessary for pass transistors, this circuit provides that function.
Brushless DC fan motors can be controlled using a variety of methods. The simplest method is on/off switching with a single transistor. Digitally programmable variable control can be achieved using linear regulators or power op amps combined with DACs or using PC health monitor ICs which offer DACs with an output that can be applied to an amplifier for driving a fan. PWM fan control chips are available that require a DAC for digital interface. Note that PWM methods have to be used with some caution.
The newest developments for fan control are digital interface ICs with complete fan driver circuits, such as the MAX1669, which include everything except for the power transistor. The MAX6650/MAX6651 take the forefront in advanced fan control because these devices are truly fan speed regulators.
The MAX1669 represents the most common type of fan control available, providing either a linear DAC output or a PWM output. It stands out because it includes a remote-junction temperature sensor input that can be connected to ICs equipped with sensing junctions or to bipolar transistors, such as 2N3904s, used as remote sensors. The MAX1669 is especially suited in situations where the fan cannot be equipped with a tachometer output because of either cost or technical requirements. Figure 1 is an example of the MAX1669 used for linear control of a fan.

Figure 1. Typical circuit for linear control of a fan using the MAX1669.
Fan Control Problems and Solutions
A big problem in fan control is the nonlinear behavior of the fan with respect to input voltage. As shown in the graph in Figure 2, the typical fan does not even begin to rotate until voltages between 3V to 8V is applied, depending on the fan. And even for a given fan, this exact voltage is subject to variations from fan to fan, and with temperature and age. When using a part such as the MAX1669, with simple fan driver amplifiers or PWM output, fans must be commanded to full speed briefly before programming low speeds. It is difficult to predict, and subject to wide variation, just how low the low speed can be. With lengthy evaluation, a minimum could be found for any fan. No matter what speed the fan is programmed to, this is an open-loop system that does not regulate fan speed.
Figure 2. This graph depicts typical fan speed vs. applied voltage.
This lack of predictability of threshold voltages has given birth to some "Rube Goldberg" schemes among some of the fan control ICs. For instance, one IC examines whether or not the fan is rotating, and if it isn't, it raises the drive incrementally. If the fan still isn't rotating it raises it another increment and so on until the fan starts.
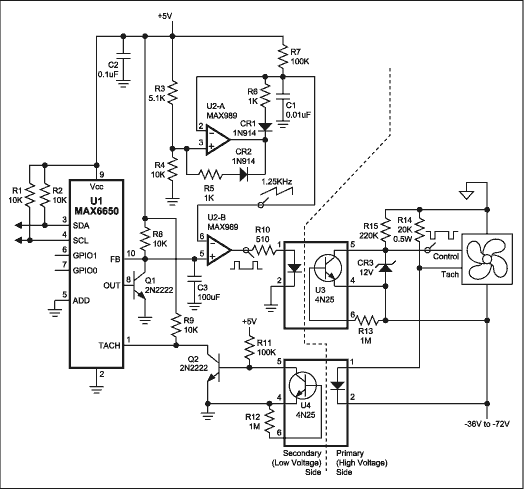
The MAX1669, along with a tachometer feedback amplifier, offers a "clean" solution to this problem by regulating fan speed (Figure 3). This trades complexity along with the effort of designing the fan control amplifier. The feedback loop of the fan control amplifier contains both differentiation and integration, the time constants of which have to be found empirically for a given make and model of fan (once found, they can be fixed for production). This additional circuit adds cost in with its higher component count.

Figure 3. Using this fan control amplifier with the MAX1669 will provide full range linear regulation (as opposed to fan control) of fans equipped with tachometer outputs.
Regulating Fan Speed
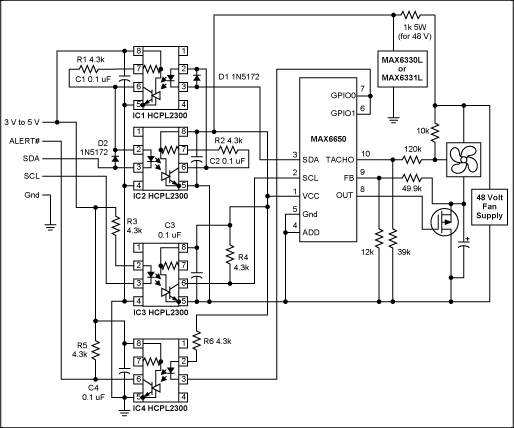
Maxim's newest fan controllers, the MAX6650 and MAX6651, make fan speed regulation possible. The MAX6650/MAX6651 are closed-loop fan control ICs designed to accept feedback from the tachometer output of a fan. This makes programming fan speed straightforward without the user having to worry about startup or slow speed reliability issues. Although both the MAX6650/MAX6651 can drive multiple fans (with tach feedback from only one of those fans), the MAX6651 has a provision to monitor the tachometer signals of up to four fans.
Figure 4. The MAX6650 is a true fan speed regulator, by virtue of including a tachometer output fan in its feedback loop.
Figure 4 depicts a typical application for the MAX6650. The MAX6650 regulates fan speed based on a code programmed into its fan speed register, by forcing the fan tachometer period to be equal to the scaled register value. Because typical fans produce two tachometer pulses per revolution, the required fan speed register value is calculated as:

where:
KTACH = Value programmed into the fan speed register
tTACH = Period of the tachometer signal
KSCALE = Prescalar value (set in configuration register of the MAX6650/MAX6651 from 1 to 16 with a default of 4)
fCLK = MAX6650/MAX6651 clock frequency (254kHz typ)
Other Advantages of the MAX6650/MAX6651
The MAX6650/MAX6651 not only regulate fan speed, but also perform a wealth of other functions. There are watchdog functions that detect when the control loop is not regulating, when fan speeds are beyond programmed watchdog limits, and other general purpose digital functions. Since these subjects are beyond the scope of this article, refer to the MAX6650/MAX6651 data sheet for details on all other functions.The MAX6650/MAX6651 free the designer from the complex issues associated with closed-loop amplifier design, leaving only selection and installation of the pass transistor.
A resistive load, linear, control pass element will be subject to maximum dissipation when delivering half the total supply voltage across the load. But does a resistive load represent a good model for fans? The graph in Figure 4 answers this question and shows that modeling the fan as a resistive load would be more demanding than the actual real-world fan behavior would indicate. This suggests that conservative design practice can treat the fan as a resistive load with the only consequence being a choice of a larger pass transistor than might be used with careful fan characterization.
Figure 4 shows that as supply voltage increases, the fan current is nonlinear and always below the current equivalent to what a resistor would draw (sized according to full fan voltage and current). For instance, the Papst fan drew approximately 240mA at 12V. An equivalent resistance would consume 120mA at the half-voltage output point and correspond to a dissipation of 0.72W:

where PD represents worst-case resistive load dissipation.
Note from the graph of Figure 4 that the real-world Papst motor showed a true dissipation of 0.65W on the pass element. Even more revealing is the current behavior of the Superred fan, which steps down to a very low level at around 6V. A conservative design that considers the fan a resistive load would have quite a bit of safety margin with the Superred fan.
Once a given pass transistor has been selected, if the following equation is satisfied then no additional heatsinking is necessary:

where:
TJMAX = Maximum allowable junction temperature from transistor manufacturer's data sheet.
TA = Maximum expected ambient temperature.
PD = Power dissipation (same as Equation 3 above).
θJ-A = Thermal resistance, junction to ambient, from transistor manufacturer's data sheet.
If the equation is not satisfied, a heatsink must be selected to satisfy the following:
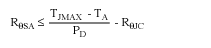
where:
RθSA = Heatsink thermal resistance (from heatsink manufacturer's data sheet).
RθJC = Pass transistor junction-to-case thermal resistance (from pass transistor manufacturer's data sheet).
The possibility of a total short circuit across the fan has not been discussed. If this happens, then the full current available from the fan power supply will flow through the pass transistor. If this condition is a consideration, then that current and voltage value should be used in all the power dissipation and heatsinking calculations. Alternatively, current limiting circuitry could be included on the pass transistor, such as the circuit shown in Figure 5. Calculate the value of the current limit resistor according t

where ILIMIT is the desired value of current limit. Note that this current limit circuit is temperature sensitive. The 0.6 term in the equation is actually the base-emitter voltage of the current limit transistor which varies according to -2.2mV/°C. This can be useful in that it acts to reduce the current limit as temperature rises.

Figure 5. When current limiting is necessary for pass transistors, this circuit provides that function.
 电子发烧友App
电子发烧友App





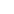













评论