近日,研究人员利用基于神经网络的新算法,成功interwetten与威廉的赔率体系 了量子系统的“稳态”。利用神经网络估计并模拟波函数和密度矩阵,大大降低了计算复杂度和算力需求,为解决量子科学和信息领域的几个突出问题打下了基础。
即使是在日常生活中,大自然也受到量子物理定律的支配。这些定律解释了生活中的常见现象,如光、声、热,甚至是台球桌上球的运动轨迹。这些日常都是符合大众视觉和想象的,我们都已经习以为常。但是当涉及到大量相互作用的粒子时,量子物理定律所解释的现象,大部分和我们的直觉相违背。
为了研究由大量粒子组成的量子系统,物理学家必须首先能够模拟这类系统。解释量子系统内部运行机制的方程可以由超级计算机解出,但是,虽然摩尔定律预测,计算机的处理能力每两年翻一番,但这与解决量子物理面临的挑战所需的计算能力相去甚远。
造成这个困难的原因是,预测量子系统的本质是非常复杂的,要想跟上量子系统规模的增长,计算力需要呈指数增长。这是一项“本质上极其复杂”的任务。EPFL纳米系统理论物理实验室负责人Vincenzo Savona教授表示。
“对于开放式量子系统,情况会变得更加复杂,因为系统会受到周围环境的干扰,”萨沃纳补充道。非常需要有效模拟开放量子系统的工具,因为量子科学和威廉希尔官方网站 的大多数现代实验平台都是开放系统,物理学家一直在寻找新的方法来对这些系统模拟和测试。
近日,洛桑联邦理工学院(EPFL)的研究人员采用神经网络模拟量子系统的新计算方法,已经取得了重大进展。相关研究成果已在“物理评论快报”的三篇论文中发表。
论文摘要:
对开放量子系统性质的模拟,是解决量子科学和信息领域的几个突出问题的前提。这个问题的难度在于系统的密度矩阵会随着系统规模的增大呈指数级增长。本文提出一种变分方法,利用变分蒙特卡罗方法和密度矩阵的神经网络,有效模拟了马尔可夫开放量子系统的非平衡稳态。
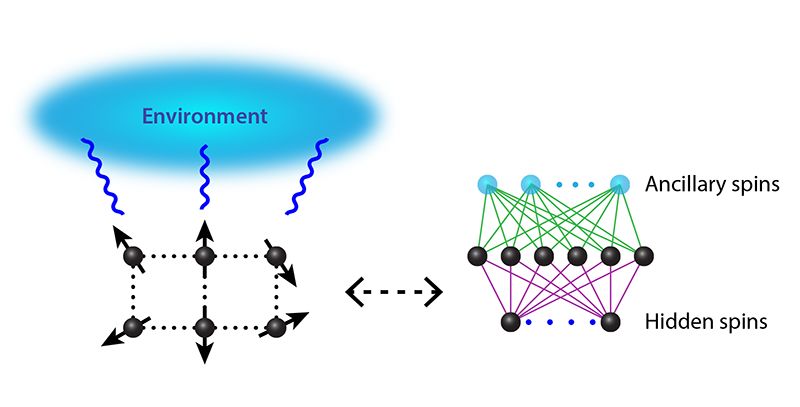
利用神经网络(右)找到“开放”量子系统的静止稳态(左)
在开放量子系统中,研究人员的目标是找到“稳态”,即不随时间变化的量子态。确定这种状态的形式理论已经存在。当系统包含多个量子粒子时,计算上可能会出现困难。要描述整个自旋系统,必须确定2^N种可能的状态。仅仅存储20次旋转的这些信息需要大约8千兆字节的RAM,并且每增加一次旋转,所需算力就会翻倍。在开放系统中处理相同数量的旋转甚至更难,因为旋转必须用“密度矩阵”ρ来描述。这个矩阵规模极大,元素数量为2^N×2^N个。
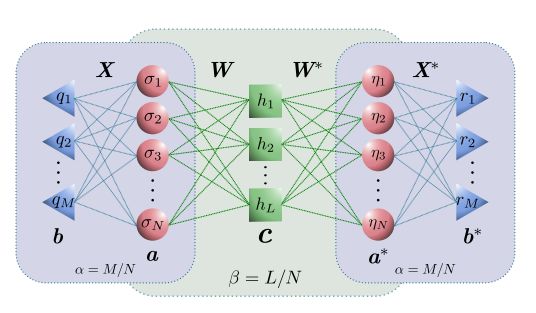
神经网络ansatz对量子系统密度矩阵的图形表示
神经网络的优势在于,它可以用很少的信息来近似模拟波函数或密度矩阵。神经网络就像一个数学“盒子”,将一串数字(矢量或张量)作为输入,并输出另一个字符串。对于模拟N量子系统的特定任务,神经网络函数可以作为波函数的“猜测”,将N个对象的状态作为输入。然后,研究人员让网络从实际或模拟数据进行“学习”,或将波函数决定的物理量进行最小化,来优化函数参数。一旦获得了正确的猜测,就可用于计算其他物理属性,其参数数量远远少于2^N 。
“这个研究基本上就是将神经网络和机器学习的进步,与量子蒙特卡罗工具结合起来,”Savona说,他说的“量子蒙特卡罗工具”指的是物理学家用来研究复杂量子系统的大型算法工具包。科学家训练了一个神经网络来同时表示多个量子系统,可以通过其环境的影响投射的许多量子态。
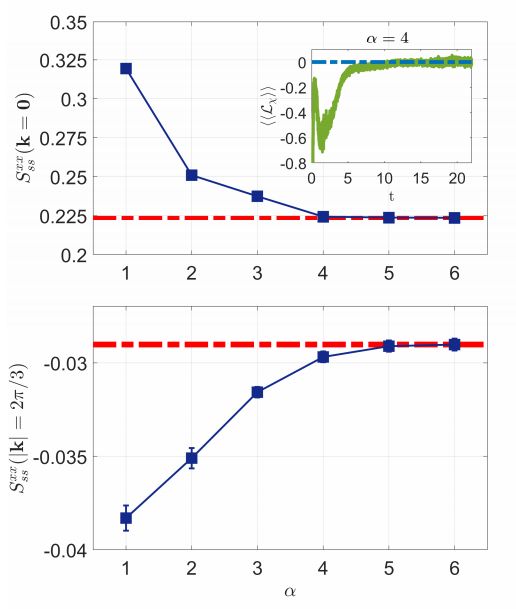
稳态自旋结构因子作为α=β的函数计算为3×3点阵,k = 0(上图)和k =(2π/ 3,0)(下图)
这一基于神经网络的方法能够让物理学家预测相当大小的量子系统的性质。“这种新算法解决了开放式量子系统的问题,具有多功能性和扩展的潜力,”萨沃纳说。该方法将成为研究复杂量子系统的首选工具,而且未来可以产生更多工具,比如评估噪声干扰对量子硬件系统的影响。
-
神经网络
+关注
关注
42文章
4773浏览量
100890 -
算法
+关注
关注
23文章
4620浏览量
93046 -
量子系统
+关注
关注
0文章
21浏览量
2632
原文标题:算法巨大突破!AI神经网络能模拟量子系统了
文章出处:【微信号:AI_era,微信公众号:新智元】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐




 基于神经网络的新算法成功模拟量子系统的“稳态”!
基于神经网络的新算法成功模拟量子系统的“稳态”!










评论