高通滤波器与低通滤波器电路完全相反,因为两个元件已经互换,滤波器输出信号现在从电阻器上取出
低电平滤波器电路通过滤波器只允许信号通过低于其截止频率点ƒc,顾名思义,无源高通滤波器电路只传递高于所选截止点的信号,ƒc 消除波形中的任何低频信号。考虑下面的电路。
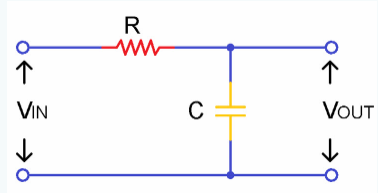
高通滤波器电路
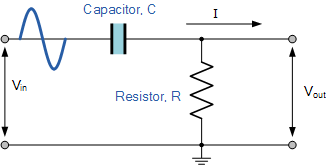
在此电路布置中,电容的电抗在低频时非常高,因此电容就像开路一样,在 V IN 时阻止任何输入信号,直到截止频率点(到达ƒ C )。在这个截止频率点以上,电容器的电抗已经充分降低,现在更像是一个短路,允许所有输入信号直接传递到输出端,如下面滤波器响应曲线所示。
一阶高通滤波器的频率响应

波特图或者,无源高通滤波器的频率响应曲线与低通滤波器的频率响应曲线完全相反。这里信号在低频衰减或衰减,输出增加+ 20dB / Decade(6dB / Octave),直到频率达到截止点(ƒc),再次 R = XC 。它的响应曲线从无穷大向下延伸到截止频率,输出电压幅度 1 /√ 2 = 70.7%输入信号值> -3dB(20 log(Vout / Vin))输入值。
我们也可以看到相位角(Φ)输出信号LEADS输入的信号,并且在频率ƒc时等于+45 o。此滤波器的频率响应曲线意味着滤波器可以将所有信号传递到无穷大。然而在实践中,滤波器响应不会延伸到无穷大,而是受所用元件的电气特性的限制。
使用相同的高阶滤波器的截止频率点可以找到低通滤波器的等式,但稍微修改了相移的等式,以解释正相角,如下所示。
截止频率和相移

电路增益, Av 以Vout / Vin(幅度)给出,计算公式如下:

高通滤波器示例No1
计算截止点或“断点”频率(ƒc)用于简单的无源高通滤波器,由 82pF 电容组成,与240kΩ电阻串联。

二阶高通滤波器
与低通滤波器一样,高通滤波器阶段也可以一起级联到m如图所示的二阶(两极)滤波器。
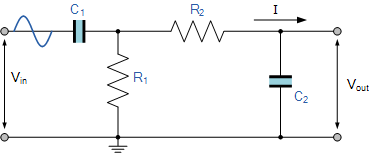
二阶高通滤波器

上述电路使用两个一阶滤波器连接或级联一起形成二阶或两极高通网络。然后,通过简单地使用额外的 RC 网络,可以将一阶滤波器级转换为二阶类型,与2 nd - 阶低通滤波器相同。由此产生的二阶高通滤波器电路的斜率为40dB / decade(12dB /倍频程)。
与低通滤波器一样,截止频率ƒc由电阻和电容确定如下。

在实践中,级联无源滤波器一起产生由于每个滤波器阶数的动态阻抗影响其相邻网络,因此难以准确地实现较大阶滤波器。但是,为了降低负载效应,我们可以将每个后续阶段的阻抗设置为前一阶段的10倍,因此 R 2 = 10 * R 1 和 C 2 = C 1 的1/10。
高通滤波器摘要
我们已经看到无源高通滤波器与低通滤波器完全相反。该滤波器没有DC(0Hz)的输出电压,直到指定的截止频率(ƒc)点。该较低的截止频率点 70.7%或-3dB(dB = -20log V OUT / V IN )允许通过的电压增益。
此截止点ƒc“低于”的频率范围通常称为阻带而“截止点”以上的频率范围通常称为通带。
高通的截止频率,转角频率或-3dB点过滤器可以使用以下标准公式找到:ƒc= 1 /(2πRC)。在ƒc处得到的输出信号的相位角是+45 o。通常,由于较高的工作频率,高通滤波器的失真小于其等效低通滤波器。
这种无源滤波器的一种非常常见的应用是在音频放大器中作为两个之间的耦合电容器音频放大器级和扬声器系统将较高频率的信号引导至较小的“高音扬声器”型扬声器,同时阻挡较低的低音信号,或者还用作滤波器以减少任何低频噪声或“隆隆”型失真。在音频应用中使用时,高通滤波器有时称为“低切”或“低音切换”滤波器。
输出电压 Vout 取决于时间如前所述,输入信号的常数和频率。通过将AC正弦信号应用于电路,其表现为简单的一阶高通滤波器。但是,如果我们将输入信号改变为具有几乎垂直阶跃输入的“方波”形信号,则电路的响应会发生显着变化并产生通常称为微分器的电路。 / p>
RC微分器
到目前为止,滤波器的输入波形被假定为正弦波或由基波信号和在频域工作的一些谐波组成的正弦波波形为我们提供过滤器的频域响应。但是,如果我们输入带有方波信号的高通滤波器,该信号在时域中工作,产生脉冲或阶跃响应输入,则输出波形将由短持续时间脉冲组成如图所示。
RC微分电路

广场的每个周期波输入波形在输出端产生两个尖峰,一个正极和一个负极,其幅度等于输入的幅度。峰值的衰减速率取决于两个分量的时间常数( RC )值( t = R x C )和输入频率的值。随着频率的增加,输出脉冲越来越像输入信号的形状。
-
电路
+关注
关注
172文章
5905浏览量
172154 -
滤波器
+关注
关注
161文章
7799浏览量
178011 -
输出电压
+关注
关注
2文章
1114浏览量
38094
发布评论请先 登录
相关推荐
无源带阻滤波器电路图,有源带阻滤波器原理图
求Sigmadsp的高阶滤波器计算公式
高通滤波器的幅频特性_高通滤波器的截止频率
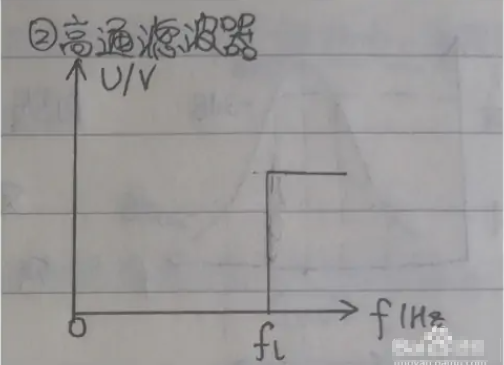




 无源高通滤波器电路频率和相移计算公式摘要
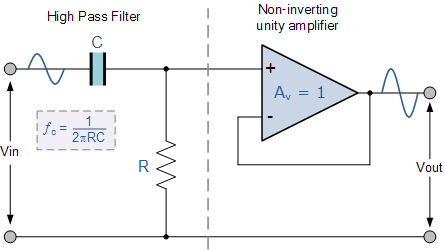
无源高通滤波器电路频率和相移计算公式摘要










评论