并行RLC电路与我们在前一个教程中看到的串联电路完全相反,尽管前面的一些概念和方程仍然适用。
然而,并行RLC电路的分析在数学上可能比串联RLC电路更困难,因此在本教程中关于并行RLC电路,本教程中仅假设纯组件使事情变得简单。
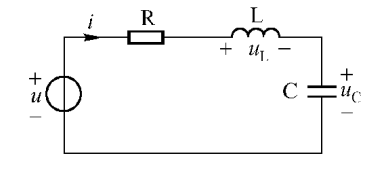
这次代替电路元件的共用电流,所有施加的电压都是共同的,所以我们需要找到通过每个元件的各个支路电流。使用类似于DC并联电路的电路的电流来计算并联RLC电路的总阻抗Z,此时的差异是使用导纳而不是阻抗。考虑下面的并行RLC电路。
并行RLC电路
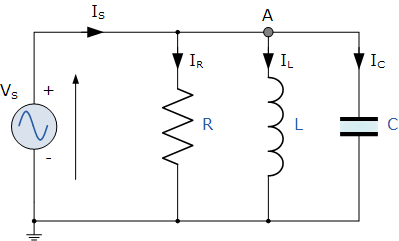
在上面的并行中在RLC电路中,我们可以看到电源电压V S 对所有三个元件都是通用的,而电源电流I S 由三部分组成。流经电阻器的电流I R ,流过电感器的电流I L 和通过电容器的电流I C 。
但是流过每个分支的电流以及每个元件的电流将彼此不同并且与电源电流I S 不同。从电源汲取的总电流不是三个独立分支电流的数学和,而是它们的矢量和。
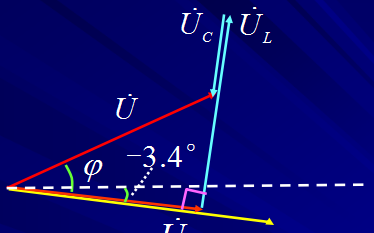
与RLC系列电路一样,我们可以使用相量或矢量方法解决这个电路,但是这个时间矢量图将电压作为其参考,其中三个电流矢量相对于电压绘制。并联RLC电路的相量图是通过将每个元件的三个单独的相量组合在一起并矢量地添加电流而产生的。
由于电路两端的电压对所有三个电路元件都是通用的,我们可以使用这个作为参考矢量,其三个电流矢量以相应的角度相对于此绘制。得到的向量 I S 是通过将两个向量加在一起得到的, I L 和 I C 然后将此总和添加到剩余的矢量 I R 。在 V 和 I S 之间获得的最终角度将是电路相位角,如下所示。
相量图并行RLC电路
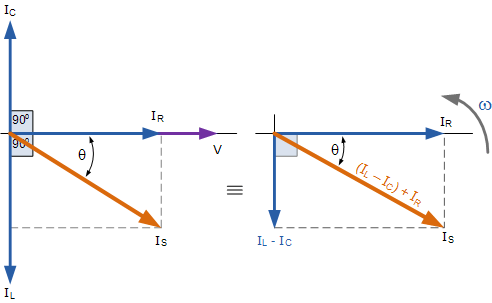
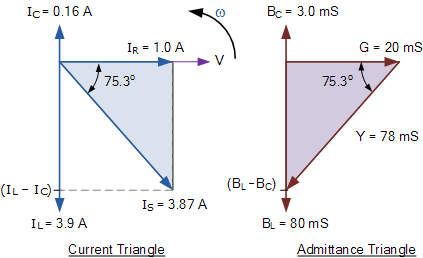
我们可以从右上方的相量图中看到当前矢量产生一个矩形三角形,包括斜边 I S ,水平轴 I R 和垂直轴 I L -I C 希望您会注意到,这会形成当前三角形,因此我们可以使用毕达哥拉斯定理当前三角形以数学方式获得沿x轴和y轴的分支电流的大小,然后确定这些分量的总电流I S ,如图所示。
当前三角形对于并联RLC电路
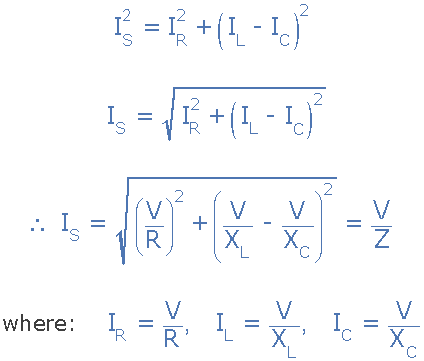
由于电路两端的电压对所有三个电路元件都是通用的,因此电流通过每个麸皮ch可以使用Kirchoff的Current Law(KCL)找到。基尔霍夫的现行定律或结法规定“进入结点或节点的总电流与离开该节点的电流完全相同”,因此进出节点“A”的电流如下:
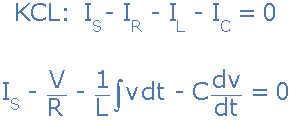
取导数,用 C 除以上式并重新排列给出以下二 - 电路电流的等式。它成为二阶方程,因为电路中有两个电抗元件,电感和电容。
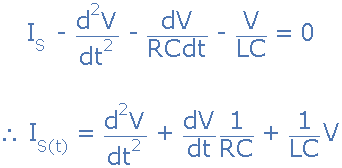
在这种类型的交流电路中对电流的反对由三个部分组成: X L X C 和 R ,这三个值的组合给出了电路阻抗, Z 。我们从上面知道,并联RLC电路的所有组件中的电压具有相同的幅度和相位。然后,每个元件的阻抗也可以根据流过的电流和每个元件的电压进行数学描述。
并联RLC电路的阻抗
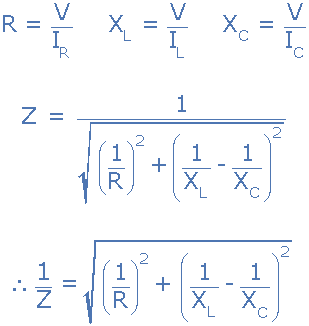
您会注意到,并联RLC电路的最终公式为每个并联支路产生复阻抗,因为每个元件都成为阻抗的倒数,( 1 / Z )阻抗的倒数被称为导纳。
在并联交流电路中,使用导纳更方便,符号( Y )用于解决复杂的分支阻抗,特别是当涉及两个或多个并联分支阻抗时(有助于数学运算)。通过添加并行导纳可以简单地找到电路的总导纳。那么电路的总阻抗 Z T 因此如图所示 1 / Y T Siemens。 / p>
并行RLC电路的导纳
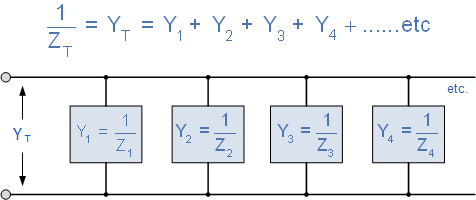
新的准入单位是 Siemens ,缩写为 S ,(旧单位mho的℧,欧姆相反)。导纳在并行分支中加在一起,而阻抗在串联分支中加在一起。但是,如果我们可以得到阻抗的倒数,我们也可以得到电阻和电抗的倒数,因为阻抗由两个分量组成, R 和 X 。然后将电阻的倒数称为电导,电抗的倒数称为电阻。
电导,导纳和电纳
用于电导,导纳和电纳的单位都是相同的,即西门子(S),也可以认为是互惠的欧姆或欧姆 -1 ,但用于每个元素的符号是不同的,在纯组件中,它的给出如下:
导纳(Y):
导纳是阻抗的倒数, Z ,并给出符号 Y 。在交流电路中,导纳定义为在施加电压时考虑到电压和电流之间的相位差,由电阻和电抗组成的电路允许电流流动的容易程度。
并联电路是相量电流与相量电压的比值,导纳的角度与阻抗的角度相反。
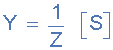
电导(G):
电导是电阻的倒数, R 并给出符号 G 。电导定义为当施加AC或DC电压时电阻器(或一组电阻器)允许电流流动的容易程度。
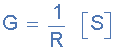
接受(B):
接受是...的倒数一个纯电抗, X ,并给出符号 B 。在交流电路中,电纳被定义为当施加给定频率的电压时电抗(或一组电抗)允许交流电流流动的容易程度。
电纳与电抗符号相反所以电容电纳 B C 为正值,(+ ve)为值,而电感电纳 B L 为负, (-ve)in value。
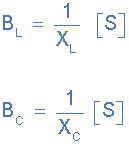
因此,我们可以将感应和电容电纳定义为:
在AC串联电路中,电流的阻抗是阻抗, Z 有两个组件,电阻 R 和电抗, X ,从这两个组件我们可以构造一个阻抗三角形。类似地,在并联RLC电路中,导纳 Y 也有两个分量,电导, G 和电纳, B 。这使得构建导纳三角形成为可能,其具有水平电导轴, G 和垂直电纳轴 jB ,如图所示。
并联RLC电路的导纳三角
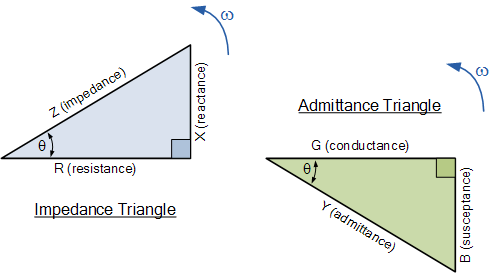
现在我们有一个导纳三角形,我们可以使用毕达哥拉斯来计算所有三个边的大小以及相位角,如图所示。
来自毕达哥拉斯
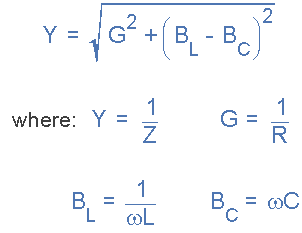
然后我们可以定义电路的导纳和相对于导纳的阻抗:
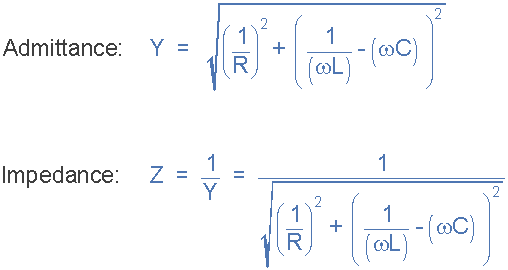
给我们一个功率因数角:
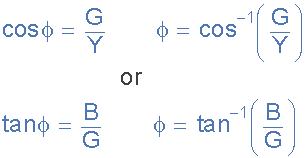
作为导纳,并行RLC电路的 Y 是一个复杂的数量,对应于串联电路的阻抗 Z = R + jX 的一般形式的导纳将写为 Y = G - jB ,用于并联电路,其中实部 G 是电导,虚部 jB 是th e。电纳。极性形式如下:
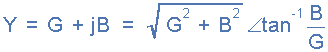
并联RLC电路示例No1
A 1kΩ电阻, 142mH 线圈和 160uF 电容均通过240V,60Hz电源并联。计算并联RLC电路的阻抗和从电源汲取的电流。
并联RLC电路的阻抗
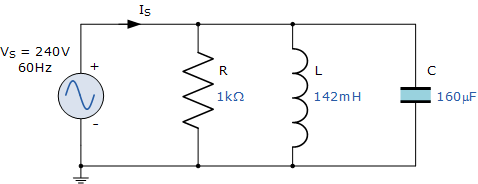
在交流电路中,电阻不受频率的影响,因此 R =1kΩ
感应电抗,( X L ):

电容电抗,( X C ):
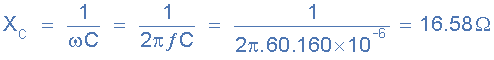
阻抗, ( Z ):
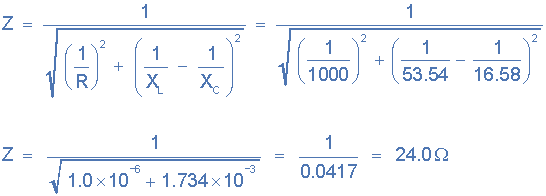
供应电流,( ):
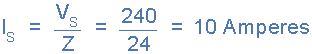
并联RLC电路示例No2
50Ω电阻, 20mH 线圈和 5uF 电容器均通过50V,100Hz电源并联连接。计算从电源汲取的总电流,每个支路的电流,电路的总阻抗和相角。同时构造代表电路的电流和导纳三角形。
并联RLC电路
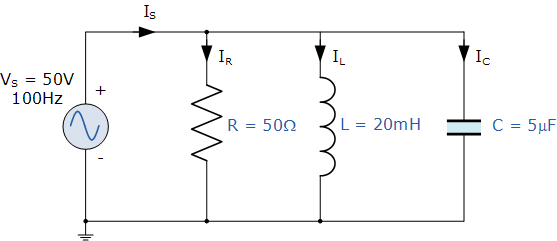
1)。感应电抗,( X L ):
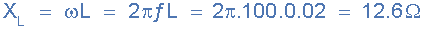
2)。电容电抗,( X C ):
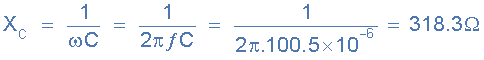
3)。阻抗,( Z ):
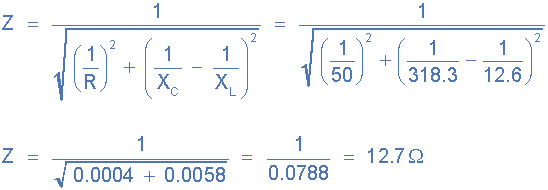
4)。电流通过电阻,R( I R ):
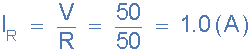
5)。通过电感的电流L( I L ):
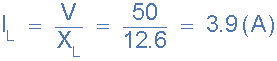
6)。电流通过电容C( I C ):

7)。总供电电流,( I S ):
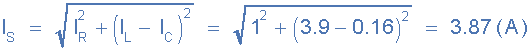
8)。电导,( G ):
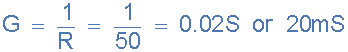
9)。感应式电纳,( B L ):
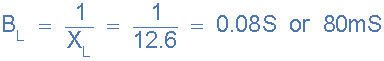
10)。电容电纳,( B C ):
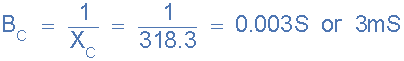
11)。准入,( Y ):
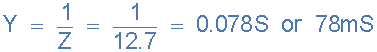
12)。合成电流和电源电压之间的相角(φ):
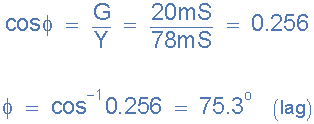
电流和导纳三角形
并联RLC电路概述
在并联RLC电路中包含电阻,电感和一个电容器,电路电流 I S 是由三个分量组成的相量和, I R , I L 和 I C ,所有三个电源电压共用。由于电源电压对所有三个元件都是通用的,因此在构造电流三角形时,它可用作水平参考电压。
可以使用与串联RLC电路相同的矢量图分析并行RLC网络。然而,当并联RLC电路包含两个或更多个电流分支时,对于并联RLC电路的分析在数学上比对于串联RLC电路更难。因此,可以使用称为导纳的阻抗的倒数来容易地分析AC并联电路。
导纳是给定符号 Y 的阻抗的倒数。与阻抗一样,它是由实部和虚部组成的复数量。实部是电阻的倒数,称为电导,符号 Y ,而虚部是电抗的倒数,称为电纳,符号 B 并以复数形式表示为: Y = G + jB ,两个复阻抗之间的对偶性定义为:
我们已经看到了该串联和并联RLC电路在同一电路中包含容抗和电抗。如果我们改变这些电路的频率,那么必须使容性电抗值等于感抗的频率,因此 X C = X L .由于电纳是电抗的倒数,在感应电路中,感应电纳, B L 的值为负值,在容性电路中,容性电纳, B C 的值为正值。与 X L 和 X C 完全相反。
发生这种情况的频率点称为共振,在下一个教程中,我们将研究串联谐振以及它的存在如何改变电路的特性。
-
电路
+关注
关注
172文章
5906浏览量
172177 -
电流
+关注
关注
40文章
6852浏览量
132138 -
阻抗
+关注
关注
17文章
957浏览量
45929 -
电压
+关注
关注
45文章
5601浏览量
115727 -
并行
+关注
关注
0文章
80浏览量
18840
发布评论请先 登录
相关推荐
威廉希尔官方网站 干货!一文读懂电源威廉希尔官方网站 之RLC电路分析
射频导纳液位计及测量原理概述
电源威廉希尔官方网站 之RLC电路分析(一)
电源威廉希尔官方网站 之RLC电路分析(二)
基本元件并联的交流电路与正弦交流电路的计算举例
电源威廉希尔官方网站 之RLC电路分析
正弦交流电路的阻抗、导纳及等效转换




 并行RLC电路阻抗和导纳定义案例概述分析
并行RLC电路阻抗和导纳定义案例概述分析










评论