前言
前两篇文章介绍了PCA(主成分分析方法)和SVD(奇异值分解)的算法原理,本文基于scikit learn包介绍了PCA算法在降维和数据重构的应用,并分析了PCA类与sparsePCA类的区别。由于PCA算法的特征值分解是奇异值分解SVD的一个特例,因此sklearn工具的PCA库是基于SVD实现的。
本文内容代码链接:
https://github.com/zhangleiszu/machineLearning/tree/master/PCA
目录
1. PCA类介绍
2. sklearn.decomposition.PCA的参数说明
3. sklearn.decomposition.MiniBatchSparsePCA的参数说明
4. PCA类在降维的应用
5. PCA类与MiniBatchSparsePCA类的区别
6. PCA在数据重构的应用
7. 总结
1. PCA类介绍
所有PCA类都在sklearn.decompostion包中,主要有以下几类:
1) sklearn.decompostion.PCA:实际项目中用的最多的PCA类;
2) sklearn.decompostion.IncrementPCA:PCA最大的缺点是只支持批处理,也就是说所有数据都必须在主内存空间计算,IncrementalPCA使用多个batch,然后依次调用partial_fit函数,降维结果与PCA类基本一致 。
3) sklearn.decomposition.SparsePCA和sklearn.decomposition.MiniBatchSparsePCA:SparsePCA类和MiniBatchSparsePCA类算法原理一样,都是把降维问题用转换为回归问题,并在优化参数时增加了正则化项(L1惩罚项),不同点是MiniBatchSparsePCA使用部分样本特征并迭代设置的次数进行PCA降维 。
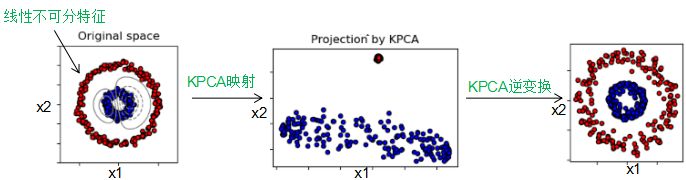
4) sklearn.decomposition.KernelPCA:对于线性不可分的特征,我们需要对特征进行核函数映射为高维空间,然后进行PCA降维 。流程图如下:
2. sklearn.decomposition.PCA类的参数说明
1) n_components:取值为:整形,浮点型,None或字符串。
n_components为空时,取样本数和特征数的最小值:
n_components == min(n_samples , n_features)
0 < n_components < 1时,选择主成分的方差和占总方差和的最小比例阈值,PCA类自动计算降维 后的维数。
n_components是大于等于1的整数,设置降维后的维数 。
n_components是字符串'mle',PCA类自动计算降维后的维数 。
2) copy:布尔型变量 。表示在运行时是否改变训练数据,若为True,不改变训练数据的值,运算结果写在复制的训练数据上;若为False,则覆盖训练数据 ,默认值为True。
3) whiten:布尔型变量 。若为True,表示对降维后的变量进行归一化;若为False,则不进行归一化 ,默认值为False。
4) svd_solver:字符串变量,取值为:'auto','full','arpack','randomized'
randomized:如果训练数据大于500×500,降维后的维数小于数据的最小维数0.8倍,采用加快SVD的随机算法 。
full:传统意义上的SVD算法,调用scipy.linalg.svd类。
arpack:调用scipy.sparse.linalg.svds类,降维后的维数符合:
0 < n_components < min(X.shape)
auto:自动选择最适合的SVD算法。
类成员属性:
components_:主成分分量的向量空间 。
explained_variance_:向量空间对应的方差值 。
explained_variance_ratio_:向量空间的方差值占总方差值的百分比 。
singular_values:向量空间对应的奇异值 。
3.sklearn.decomposition.MiniBatchSparsePCA的参数说明
本节就介绍两个常用的重要变量,用法与PCA类基本相同。
n_components:降维后的维数
alpha:正则化参数,值越高,主成分分量越稀疏(分量包含0的个数越多)。
4. PCA类在降维的应用
Iris数据集包含了三种花(Setosa,Versicolour和Virginica),特征个数为4。
下载Iris数据集:
iris = datasets.load_iris()X = iris.datay = iris.target
设置降维后的维数为2:
pca = PCA(n_components=2)
降维后的数据集:
X_r = pca.fit(X).transform(X)
降维后的特征分布图:
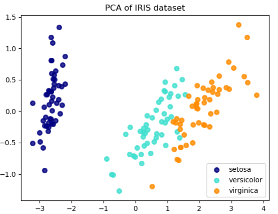
5. PCA类与MiniBatchSparsePCA类的区别
PCA类主成分分量是非零系数构成的,导致了PCA降维的解释性很差,若主成分分量包含了很多零系数,那么主成分分量可以将很多非主要成分的影响降维0,不仅增强了降维的解释性,也降低了噪声的影响 ,缺点是可能丢失了训练数据的重要信息。MiniBatchSparsePCA与PCA类的区别是使用了L1正则化项,导致了产生的主成分分量包含了多个0,L1正则化系数越大,0的个数越多,公式如下:
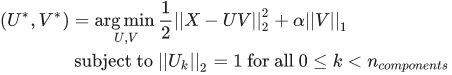
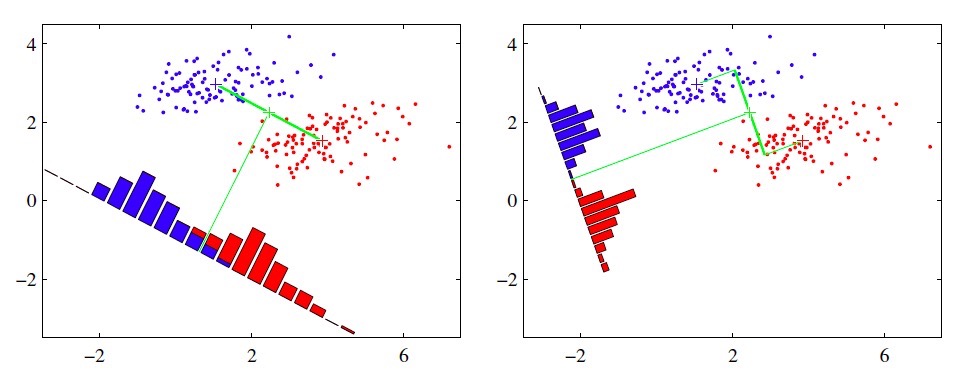
用图来说明区别:
左图是PCA类的主成分分量空间,右图是MiniBatchSparsePCA类的主成分分量空间,比较两图可知,右图能够定位到重要的特征部位 。
若是用数值表示,MiniBatchSparsePCA类的主成分分量值为:

由上图可知,主成分分量包含了很多零分量 。
6. PCA在数据重构的应用
数据重构算法借鉴上一篇文章的图:
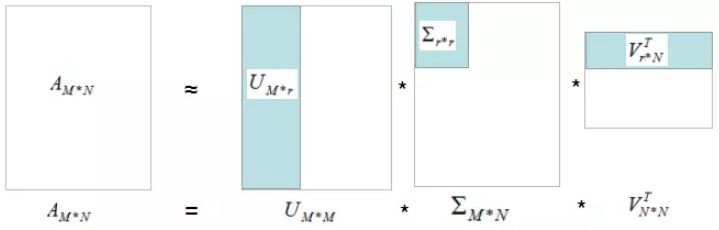
浅蓝色部分矩阵的乘积为数据的重构过程,r为选择的主成分分量个数 。r越大,重构的数据与原始数据越接近或主成分分量的方差和比例越大,重构的数据与原始数据越接近 ,图形解释如下:
n_components是0.2的数据重构图:

n_components是0.9的数据重构图:

因此,主成分分量越多,重构的数据与原始数据越接近。
7. 总结
本文介绍了PCA类在降维和数据重构的简单用法以及分析了sparsePCA类稀疏主成分分量的原理。
-
函数
+关注
关注
3文章
4329浏览量
62583 -
数据集
+关注
关注
4文章
1208浏览量
24693 -
PCA算法
+关注
关注
0文章
2浏览量
1298
原文标题:scikit learn中PCA的使用方法
文章出处:【微信号:AI_shequ,微信公众号:人工智能爱好者社区】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐

FPGA的重构方式
求助,SVM分类时要不要先进行PCA降维呢?
【FPGA学习】VHDL的数据类型类预定义属性和数据范围类预定义属性是怎么用的
可重构波束天线威廉希尔官方网站 在增加网络容量应用
为什么要重构?如何重组Python包?
基于Autoencoder网络的数据降维和重构
java并发编程实战之辅助类用法
Java数组的常用方法_Java:数组工具类Arrays类的常用方法的用法及代码
融合尺度降维和重检测的长期目标跟踪算法

STM8L定时器1和定时器4的简单用法





 PCA类在降维和数据重构的简单用法
PCA类在降维和数据重构的简单用法










评论