拓扑排序是算法课经典内容之一,但是学的时候如果只是被动接收,那就很容易沦为“算法背诵”,很快就记忆模糊了。这一次同样的,我们从主动发明的出发点去搞清楚这个问题的机理,就很难遗忘了。
跟上回一样,从发明的角度,我们只要问两点:
(1) 我们想解决一个什么问题?
(2) 这个问题如何最好地解决?
1
动机:前提关系
本文中我们想解决的各种问题,都有一个明确的共同范式:任务,和任务之间的先后顺序,或者说前提关系。有很多任务需要完成,其中有的任务开始之前,会要求某些前提任务首先被完成。
这样的具体例子很常见,生活中比如
先修课程:一系列课程,基础课可以随便修,想上稍微高级一点的课程可能会要求先修完若干门基础一点的课程。在这样“先修课程”的关系之下,怎么把一系列课全修完,就需要在顺序上有一些计划
计算机内部这样的情形更常见,比如:
软件包批量安装:安装很多软件包的时候,有的包会用到别的包,被用到就要先装,安装器就需要根据这些前提关系规划安装顺序
计算任务:设置复杂的计算任务的时候,有的计算需要用到别的计算的结果,计算框架的scheduler就需要理清这里面隐含的先后关系,才能所有结果全算出来
2
问题
所以,对这个问题合理的抽象就是,有任务,也有任务之间的依赖关系,它们之间自然会形成一个dependency graph:
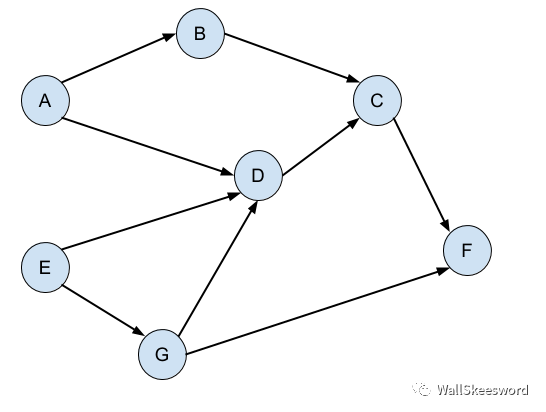
而我们想找出一种合理的任务顺序,按这个顺序依次完成任务,可以保证做到每件任务的时候,它的前提任务都已经被完成。上图中,比如 A-B-E-G-D-C-F。
3
徒手体会
先徒手操作一下,对这个问题产生一些最直观认识。其实对于人来说,这个问题没什么难度,大可以边做边想。比如当你面对一堆课程的时候(例子来源于本人将在程序员末日2038年胡乱编纂的“从入门到放弃”系列精品课程)
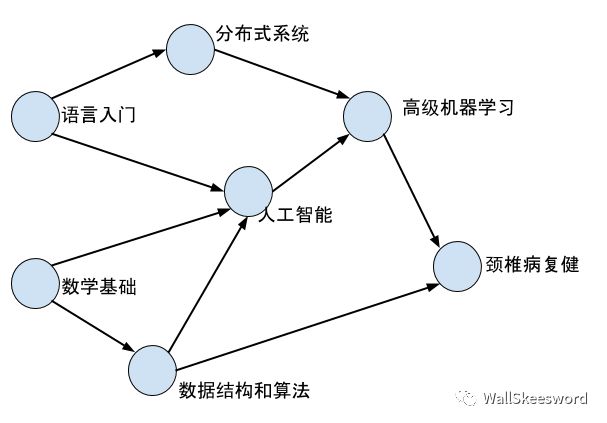
首先总该有一些课是直接可以上的,比如图中“语言入门”和“数学基础”。你完全可以选一门上就好了,比如你选“数学基础”,上完之后这门就可以抛到脑后
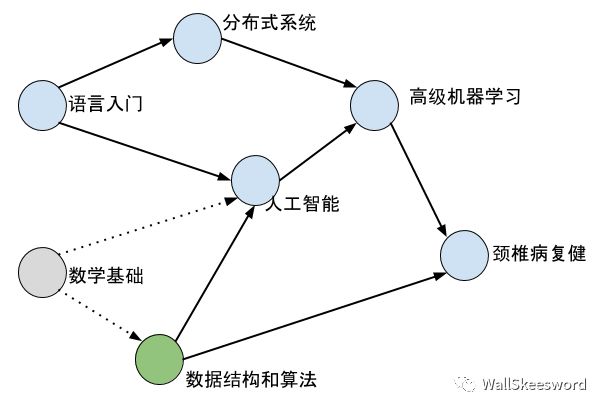
顺便这也有可能为新的课打开了大门,比如现在就新可以上“数据结构和算法”了。所以直觉来看拓扑排序并没有什么难度,只要有耐心,谁都可以一步步顺着当前可以上的课上,成功地从入门到放弃(误)。
4
初步解法
那么其实我们就已经可以有一个最原始的解法了,非常简单粗暴,但是至少可以给出正确的答案:每次重新审视这个图,一个一个检查还没完成的任务,如果哪一个任务的所有前提都已完成,下一个就做它,也就是,加入输出序列,并把这个新任务标记为完成。举例说明,比如说当你做到某一步时,来到了下图所示的这个情境中(灰色为已完成任务, 丑蓝为待完成任务)
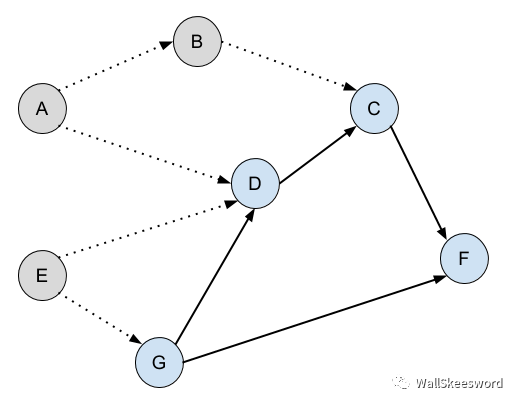
你可以一个个检查有待完成的蓝色任务们。C,它还有前提任务D没有完成;D在等G;F也不行;G,诶,它的前提任务都已完成,好,那就它了。下一个输出G,并且把它标为已完成。
如此往复,最终总能把所有任务都有条不紊地完成。
作为最原始的解法,它的效率不高。但是这并没有关系,找到其中的浪费,一个个解决,自然就可以迭代出一个好的解法。
5
优化:去掉浪费
浪费1
首先,“检查前提任务有没有都完成”这个步骤,可以简洁一点。每个结点可以一直记着自己还有几个前提任务没有完成(结点的入度)。比如下图,蓝色数字标注还剩几个前提任务
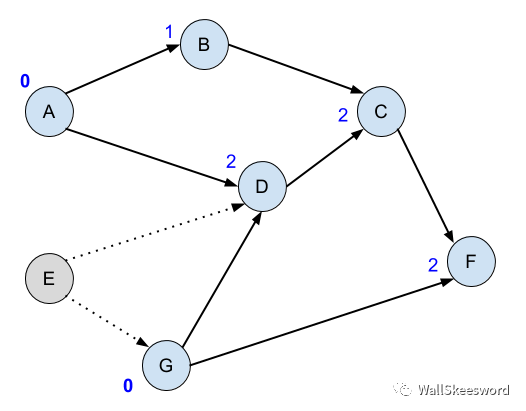
接下来,如果我们完成了A,可以去通知它的后继结点们 B 和 D,告诉它们入度可以减1了。这样,你只要看一个任务的未完成前提数有没有降到0,就知道这个任务是不是可做。
浪费2
我们的流程还有一个巨大的浪费:我们在重复寻找已ready(入度为0)的结点。接着 ↑上图↑ 的情形,我们发现A和G已经入度为0,处于ready状态;假设我们接下来选择做A,于是 B 和 D 入度减1:
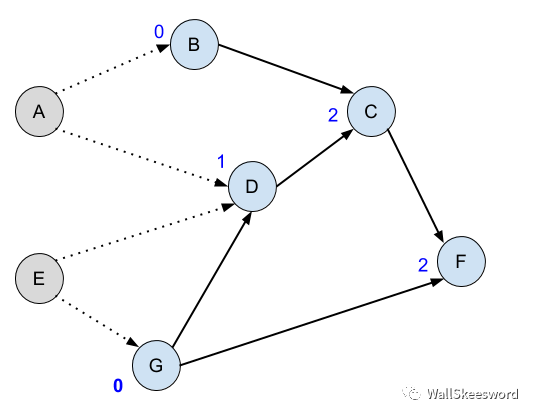
然后下一轮的时候,我们还需要遍历所有蓝色结点,去寻找那些ready的吗?不需要:
我们上一轮就知道G的入度为0的,现在肯定没变过
只有 A 的后继 B 和 D 的入度发生了下降,其他的 C 和 F 这些结点完全没受影响,那它们的入度既然之前不是0,现在没变,肯定依然不是0
所以说,我们记着之前发现过的所有ready的结点,然后每次只需要在那些入度被更新的结点中寻找新的ready结点就够了。如此一来,我们去掉了大量的浪费,也得出了一个算法了——
维护一个所有ready结点组成的集合,每次从里面选一个结点完成,把它的后继的入度都减一,并在被更新的结点中找出新的ready结点,加入我们的集合。
6
标准解法 BFS
这样子迭代优化出来的做法,其实就是拓扑排序所谓的BFS解法。我们用具体的例子直观地描述一遍。
初始化的时候,计算每个结点的入度,所有初始入度就为0的结点,都是处于ready状态的任务,加入我们的集合(图中标为丑绿)
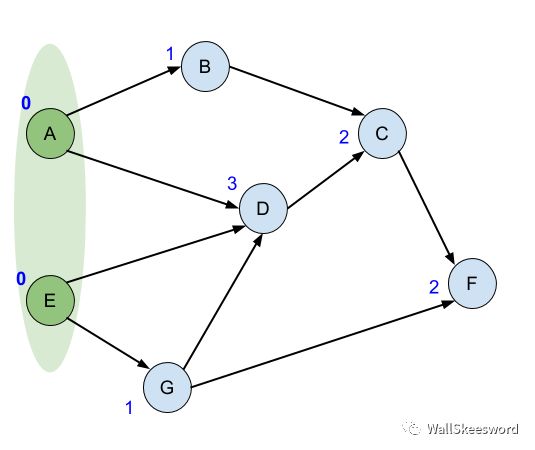
接下来每一次,从绿色ready集里面随便拿一个结点出来,比如 A,这个任务已经处于ready状态,所以完成它(输出);A任务完成以后,它的后继结点 B 和 D 的入度都可以去掉 1,如果有哪个后继结点在这个过程中入度降成了0 (比如B),那它也进入了ready状态,我们就顺手把它加入我们的ready集合。
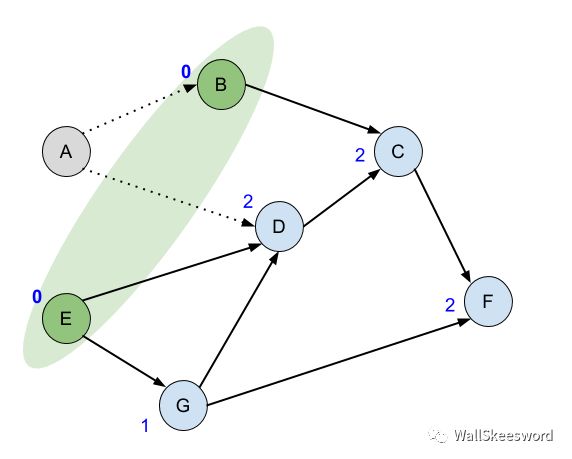
如此这般,循环下去,每次找到下一个可以做的任务,可以一路把拓扑排序输出出来。
图看完了,再用迷幻的伪代码描述一下:
初始化1:每个结点把自己的入度数好[乖巧]初始化2:建立一个ready集合,记录下哪些结点已经ready.把一开始入度就为0的源点都加入集合接下来只要集合里还有结点: 1. 从集合里随便拿一个结点v出来 2. 把v输出,并且通知它的所有后继:你们的前提任务又少了一个,快把入度-1 3. 在顺序通知的同时,如果哪个后继发现自己的前提任务因此全部达成(入度降到0),就把自己加入ready大家庭如此往复,就获得了这个图的一个拓扑排序。
这样一来,这个循环中,每条边都正好被用到一次(为什么?),浪费已经降到最小,我们知道已经达到效率最优解了。
7
标准解法 DFS:目标导向
我很久以前首次接触这个问题的时候,发明的就是上面BFS的解法,因为它符合事物自然推进的顺序,“捡当前能做的东西做”。一直到大学的时候我才知道,原来有简便得多的方法,虽然理论复杂度相同,但想起来、写起来都要简洁很多,这就是拓扑排序的所谓DFS解法。非常有意思的是,这个解法来自于“从目标出发,一步步倒推”的结果导向型思路。
怎么说呢,就是面对一个dependency graph,我不是循序渐进捡ready的任务做,而是随手指一个结点,比如下图中的 “一个亿”

然后先将其确立一个小目标,别的什么都不想,只求完成我指定的这个任务。确立“一个亿”小目标之后,就要开始倒推了,为了能完成任务“一个亿”,我得先完成它的所有前提,就是“悔创阿里”和“不知妻美”,于是乎对于每一个前提任务,你也可以同样倒推(比如为了达成成就“不知妻美”,首先要做任务“普通人家”),依次去满足他们的前提条件,一直到倒推到没有前提的任务,或者之前已经完成的任务为止。
这个自我重复的流程非常适合递归。直接上迷幻的伪代码,大家感受一下它简洁的魅力
(所有结点上都应该有个标记,标该结点是否已完成/输出过)function完成小目标(v):先看看v之前有没有被完成过1.已完成→打扰了,return2.未完成→好的,干它a)对于v的所有前提任务ui:递归调用完成小目标(ui)b)都完成之后,现在所有前提应该都已满足,就输出v,并标记为已完成
当然,为了获得全图的拓扑排序,我们还需要一个粗暴的循环——
对于图中所有结点v:调用完成小目标(v)
建议初次接触的朋友自己试几个结点感受一下,递归函数所倚靠的系统栈,如何就帮你把这个顺序问题全部解决了。
8
思考:环
以上我们就介绍完了两种常见的拓扑排序算法。
但是接触过这个问题的人都知道,对于一个有向图,首先拓扑排序是否存在都得打个问号。之前的讨论中我刻意忽略了这个问题,因为对于初学者来说,同时操心太多头绪可能会干扰思考。现在,是时候把这个问题重新加入考虑,正好也作为对之前内容的进一步思维练习。
问题:拓扑排序什么时候根本就不存在呢?
当然,举出一个没有拓扑排序的例子不难——当两个任务直接或间接互为前提条件的时候,就没法完成了,比如:
这些时候,图中都有一个“环”的存在,循环调用,互为前提。
有环就没法拓扑排序,这个比较好理解。反过来的方向,有向图如果没有环就一定有拓扑排序,需要稍微数学一点的证明,为了保持本文的flow,就跳过留给有兴趣的人自己想了。
于是乎,我们有结论,拓扑排序一定建立在“有向无环图”之上。那么怎么在算法中检查环的存在呢?也就是说,我们面对的问题变得更一般了一些,现在任务不是给定有向无环图,找出一个拓扑排序,而是:
给定一个有向图,输出拓扑排序,或者判定图中有环。
BFS解法中加入判断
回顾一下刚才的BFS解法,我们是用一个集合/容器记着所有目前已经ready的结点,每次取出一个,输出,然后在它的后继中寻找新的ready结点加入集合。那么想象在一个有环的图中会出现什么呢?
没想明白的盆友可以先自己演绎一下。
。
。
。
。
。
。
。
如果在我们之前的图中,将DE之间的边反向,则会出现图中红色标注的环。
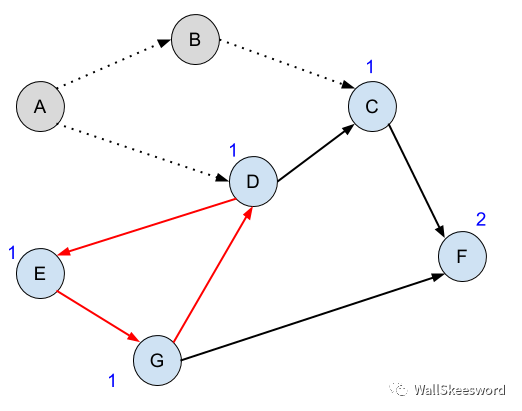
按照之前的方法运行我们的BFS算法,可以成功完成A,然后B,之后会卡在图中所示的尴尬境地:没有入度为0的结点了,所有未完成任务都要求别的任务先完成,谁也不让谁,于是我们卡在这里再也进行不下去。
所以这就是BFS中我们判断环的标准:如果算法进行到某一步,还有未完成任务,但ready集合为空,即没有任务是ready的,则一定是有环把我们卡住了。
DFS解法中加入判断
如果DFS解法遇到了有环的情况,会发生什么?如果还是用上图的红色环为例,为了完成D,你会调用如下序列
完成小目标(D)
→ 完成小目标(A),
完成小目标(G)
→ 完成小目标(E)
→ 完成小目标(D)
→ ...
你会发现这个递归进入一个死循环。所以判断图中有没有环的方法,就是想办法去发现自己的递归流程有没有重复访问同一个结点。但这其中有一些细节需要思考,比如其实访问一个已访问过的结点很多时候也是正常的——结点被访问过可能是因为被之前某个任务完成了。所以可能需要我们想办法区分这两种情形。这是一个很有意思的问题,自己想明白会很有趣,所以我们照例在最后留一点想象空间,由有兴趣朋友自己思考品玩 :)
-
拓扑
+关注
关注
4文章
341浏览量
29602 -
计算机
+关注
关注
19文章
7494浏览量
87959 -
DFS
+关注
关注
0文章
26浏览量
9165
原文标题:拓扑排序
文章出处:【微信号:TheAlgorithm,微信公众号:算法与数据结构】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
CAN总线十万个为什么 | 聊聊几种常见的CAN网络拓扑

时间复杂度为 O(n^2) 的排序算法

设计一个电源,如何考虑选择拓扑?
储能变流器的拓扑结构介绍
FPGA实现双调排序算法的探索与实践





 拓扑排序的介绍和如何使用拓扑排序解决一个问题
拓扑排序的介绍和如何使用拓扑排序解决一个问题














评论