二分法查找在实际电路中的应用

1

首先问大家一个问题，如果有一堆有序的数据

1,2,3,4,5,6,7,8,9,10,11,...100

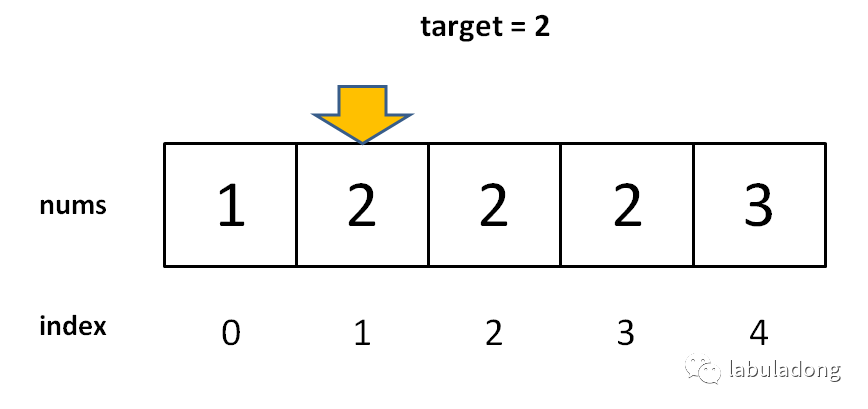
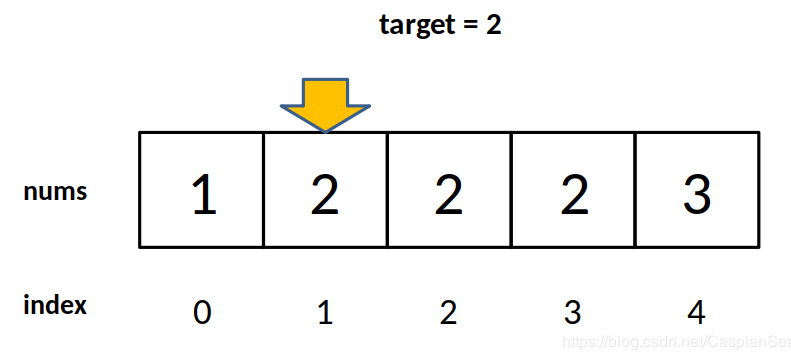
如果想要找出55，你要怎么实现呢？

最直观的是用线性查找，从头开始一个个的查找，需要55次才能找到目标数值。

如果大家学过C或者C++，应该有二分法查找的概念，先把这堆数分成2堆，把第一堆的最后一个数跟55比较，发现55比它大，所以55应该在第2堆。再重复这个过程，大概需要7次就可以确定55的位置。

二分法查找效率显而易见，它的时间复杂度T(n)=O(log(2)n)，远远小于线性查找的T(n)=O（n）。

但二分法要求数据必须是有序排列的，这在实际电路世界里面往往是满足的。

利用二进制搜索（二分法查找）实现的逐次逼近算法，每次都是选取比较范围内的中间点来跟参考值进行比较，通过比较结果来继续缩小比较范围，一直迭代直至找到最接近比较值的解。

这个过程跟求方程(近似)解也非常类似。二进制搜索实现的逐次逼近常常用于需要校准的场景中，比如SAR ADC、DRAM ZQ 校准、仪器校准算法等。因为我们的校准代码对应的值是线性增加或者减小的，符合二进制搜索法的条件。

2

下图是一个SAR ADC的基本架构：

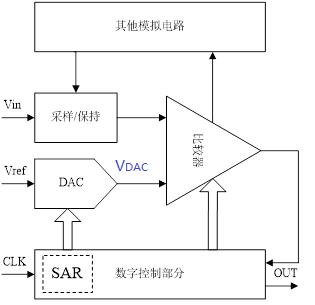
电路的目标就是得到一个最接近Vin的VDAC，可以通过调整

SAR code配置DAC模块得到。

假设我们的SAR（逐次逼近寄存器）的位数是3位，初始状态设为SAR[2:0]=3'b100，也就是处于000-111的中间位置。

如果SAR的使能clock 开始toggle，比较过程就开始了：

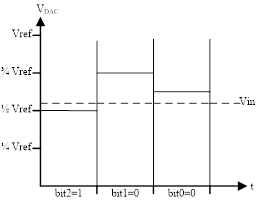
如上图所示，X轴表示时间，Y轴表示DAC输出电压VDAC：

第1次比较： 设置SAR[2:0]=3'b100，VDAC=1/2 Vref < Vin , 所以SAR[2]保持1，SAR[2:0]=3'b100；

第2次比较： 设置SAR[2:0]=3'b110，VDAC=(1/2 Vref + 1/4 Vref)> Vin , 所以SAR[1]最终取0，SAR[2:0]=3'b100；

第3次比较： 设置SAR[2:0]=3'b101，VDAC=(1/2 Vref + 1/8 Vref)> Vin , 所以SAR[0]最终取0，SAR[2:0]=3'b100；

最终我们可以得到与输入电压Vin最接近的VDAC，可以看出SAR的位数越多，精度越高，但是比较周期数也会越来越多。

另外其第3次（最后一位）比较好像也没有必要，因为你比较完也无法得到一个相等值，可以把最后一位固定成1或者0，最大的误差就是最后一位代表的权重1/8 Vref。

2

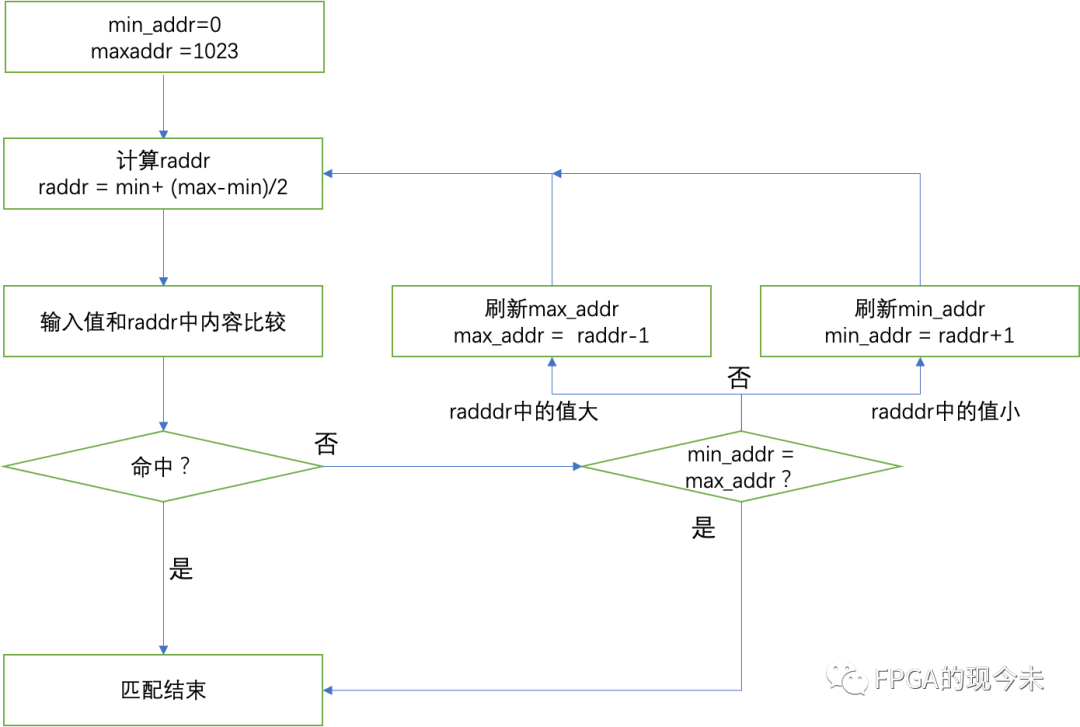
前面是具体的SAR ADC的例子，我们可以进一步把二进制搜索SAR的过程画成流程图的形式，方便后续电路或者Verilog代码的实现：

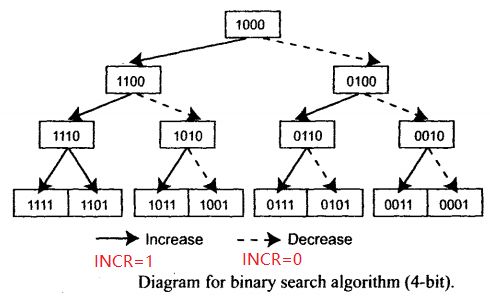
初始化SAR的MSB=1， 其它bit为0 （比如4bit 4'b1000）

每次CLK go high ，走一步

如果INCR=1， 走图中实线箭头方向；

如果INCR=0， 走图中虚线箭头方向；

最低位LSB最终固定为1

4bit的SAR 一共需要走3步，也就是3个CLK周期后就可以得到最后的结果。

3

最后给出一个6位二进制搜索SAR logic电路的SPEC：

Input

INCR

RSTB reset信号，负沿有效

CLK

OUTPUT

PUCODE [5:0]

你觉得这个电路是用Verilog代码实现呢？

还是自己搭电路比较好？