20log(N)规则
首先,是对20log(N)规则的快速回顾:
如果一个时钟的载波频率下降了N倍,那么我们预计相位噪声会减少20log(N)。例如,每个除以因子2的除法应该导致相位噪声减少20log(2)或大约6dB。这里的主要假设是无噪声的传统数字分频器。
为什么是这样?实际数字分频器的输出是上升沿和下降沿,信号处于逻辑高电平或低电平。抖动仅出现在上升沿和下降沿。抖动对每个时钟周期的比例降低。我们的直觉可能表明,如果我们减少抖动边缘的数量,那么我们减少了分频时钟传输的抖动。事实证明是正确的。
这可以写成:

相位抖动会怎样?
我们整合了SSB相位噪声L(f)[dBc / Hz],以获得以秒为单位的RMS相位抖动,如下所示:从f1到f2的偏移频率以Hz为单位进行积分,其中f0是载波或时钟频率。
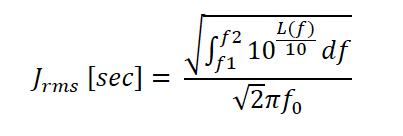
在实践中,所涉及的数量足够小,对于良好的时钟来说,对于12kHz到20MHz的抖动带宽,RMS相位抖动大约在10s到100s的飞秒数量级上。
请注意,以秒为单位的RMS相位抖动与f0成反比。当频率被分频时,相位噪声L(f)下降20log(N)。然而,由于频率也下降了N,以时间为单位表示的相位抖动是恒定的。因此,与20log(N)相关的相位噪声曲线在抖动带宽上具有相同的相位噪声形状,预计会在几秒钟内产生相同的相位抖动。
例子
我们来看一个具体的例子。作为一个实验,我拿了一个Si5345抖动衰减器,输入一个25MHz的时钟,并配置它,使我只改变一个(内部)输出分频因子2,以获得从800MHz到50MHz的频率。然后,我使用Agilent(现为是德科技)E5052B测量相位噪声,并比较了每种情况下的相位噪声和相位抖动。对每个频率对五次运行进行平均和相关。为了清楚起见,我简化了实验。
通过MSPaint的魔力和使用“Transparent Selection”功能,我可以覆盖所有的E5052B屏幕大小,如下所示。(如果运行是相同的每次只有唯一的文本被遮盖)。在下图中,轨迹通常从载波频率下降到800MHz,然后400MHz等降到50MHz。除了曲线在最高偏移频率下被压缩的地方,曲线的形状是相同的。
然后,我列出了在12kHz至20 MHz抖动带宽上测量的相位抖动结果,如下所示:
我们可以从图和表中得到两个直接的观察结果。
1. 曲线之间的距离接近于我们所期望的20log(N)规则,直到迹线开始呈现为朝向100kHz到MHz偏移。
2. 对于800 MHz到200MHz,fs的RMS相位抖动大致相同。但是,对于100MHz和50MHz的情况,与期望的相位抖动是不同的。
尽管采用了20log(N)规则,但是由于降低了输出时钟频率,尤其是在200MHz以下,相位抖动变得更糟。这些较低频率的时钟测量的远比预期抖动。因此出现了抖动分频时钟的情况。发生什么了?
由于明显的相位噪声基底而导致的曲线压缩似乎是计算的RMS相位抖动的差异的原因。我们通过比较800 MHz和100 MHz情况下10 kHz到20 MHz偏移的数据来验证。所有的相位噪声数据来自原始标记,除了从屏幕盖图估计的20MHz点之外。(请注意,对于8或23倍,我们预计相位噪声的增量为3 x 6 dB或18 dB。)
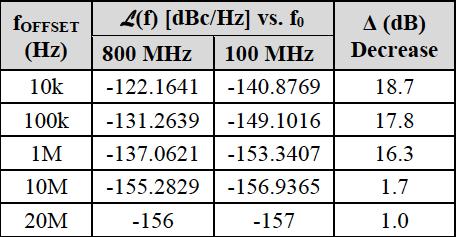
只要将这些值输入到Silicon Labs在线相位噪声抖动计算器中,我们就可以得到以下结果。

现在,让我们修改100MHz数据集,以消除较高的偏移频率压缩,如下所示。如果使用20log(N)规则,那么预期的18dBΔ也是如此。
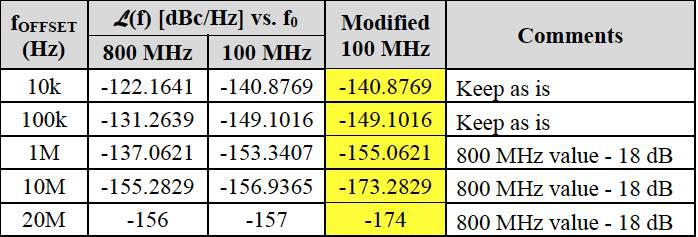
将修改后的值输入到在线计算器中,我们将其计算结果以高亮显示的方式添加到表格中:
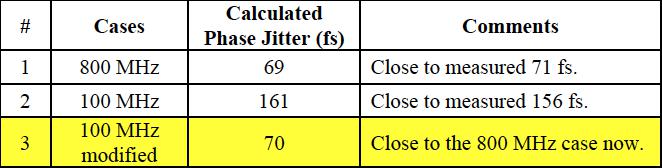
这个练习证实曲线压缩考虑了相位抖动在800 MHz和100 MHz之间测量的显着差异。
噪声基底
所有的迹线变平或接近平坦的20 MHz偏移量。那么,什么是明显的或有效的噪底?请注意,一般来说,这将是一些RSS(平方和根)组合的仪器相位噪底和DUT的远相噪声。例如,如果DUT和仪器在20MHz偏移量下的有效相位噪声为-153 dBc / Hz,则RSS结果将高出3dB或-150 dBc / Hz。
如果仪器本底噪声远低于DUT,我们预计20 MHz偏移处的点相位噪声将从800MHz时钟的测量结果中减去6 dB。但那并不是发生的。见下表和附图:
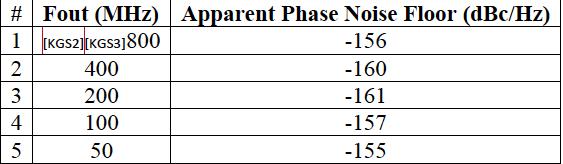
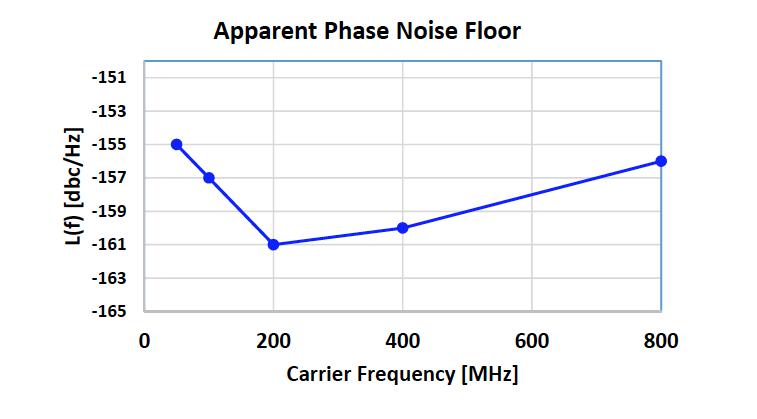
相位噪声本底不是单调变化的,这表明可能涉及多个因素。查看E5052B规格表明,随着载波频率降低,SSB相位噪声灵敏度应稍微降低。另外,来自DUT(Device Under Test)的远相噪声通常由输出驱动器的相位噪声主导,并且不可能以这种方式变化。我们很可能会将仪器的“实际”相位本底噪声作为输入频率的函数加上DUT部分的混叠来运行。 Si5345的分频器边缘可以被看作是采样分频器内部时钟的相位噪声。这个因素是独立于仪器的。可以理解的是,可能发生混叠,但是量化由于混叠引起的特定贡献可能是有问题的。
这篇文章提出,如果输入信号的噪声带宽大于4×分频器输出频率v0,则分频的PM(相位调制)噪声将通过10log [(BW/ 2v0)+1]的混叠而降低。所描述的混叠主要影响我们感兴趣的远端偏移。
写道:“宽带噪声的混叠一般对接近载波噪声的影响要小得多因为它通常比宽带噪声高很多个数量级。“
在这些特定的测量中,假定给定的BW和仪器本底噪声,对于最低载波频率估计的本底噪声是合理的。然而,似乎没有一个解决方案可以容纳所有的数据。它可能需要在最高输出频率下操作设备,然后使用外部分频器和滤波器来正确分类。也许在未来的某个帖子里。
总结
我们已经回顾了相位噪声仪表的明显的或有效相位噪底对于足够低的频率时钟的相位噪声曲线和相位抖动测量的影响。在用DUT和相位噪声设备工作一段时间之后,您将认识到典型的相位噪声曲线,设备的近似相位噪底以及相位抖动的合理预期。当然,对于上述情况,对200 MHz以下的相位抖动测量,我们不得不采取一定的措施。如果有疑问,请尝试更高频率的类似配置以进行比较。由于任何仪器本底噪声的变化和/或由于较高的分频系数导致的混叠,您只会错过次级相位噪声劣化。
-
噪声
+关注
关注
13文章
1122浏览量
47402 -
频率
+关注
关注
4文章
1497浏览量
59219 -
时钟
+关注
关注
10文章
1733浏览量
131462
发布评论请先 登录
相关推荐




 测量时钟频率的相位噪声和相位抖动时出现的问题分析
测量时钟频率的相位噪声和相位抖动时出现的问题分析












评论