简要介绍einsum表示法的概念，通过真实例子展示了einsum的表达力

编者按：FAIR研究科学家Tim Rocktäschel简要介绍了einsum表示法的概念，并通过真实例子展示了einsum的表达力。

当我和同事聊天的时候，我意识到不是所有人都了解einsum，我开发深度学习模型时最喜欢的函数。本文打算改变这一现状，让所有人都了解它！爱因斯坦求和约定（einsum）在numpy和TensorFlow之类的深度学习库中都有实现，感谢Thomas Viehmann，最近PyTorch也实现了这一函数。关于einsum的背景知识，我推荐阅读Olexa Bilaniuk的numpy的爱因斯坦求和约定以及Alex Riley的einsum基本指南。这两篇文章介绍了numpy中的einsum，我的这篇文章则将演示在编写优雅的PyTorch/TensorFlow模型时，einsum是多么有用（我将使用PyTorch作为例子，不过很容易就可以翻译到TensorFlow）。

1. einsum记法

如果你像我一样，发现记住PyTorch/TensorFlow中那些计算点积、外积、转置、矩阵-向量乘法、矩阵-矩阵乘法的函数名字和签名很费劲，那么einsum记法就是我们的救星。einsum记法是一个表达以上这些运算，包括复杂张量运算在内的优雅方式，基本上，可以把einsum看成一种领域特定语言。一旦你理解并能利用einsum，除了不用记忆和频繁查找特定库函数这个好处以外，你还能够更迅速地编写更加紧凑、高效的代码。而不使用einsum的时候，容易出现引入不必要的张量变形或转置运算，以及可以省略的中间张量的现象。此外，einsum这样的领域特定语言有时可以编译到高性能代码，事实上，PyTorch最近引入的能够自动生成GPU代码并为特定输入尺寸自动调整代码的张量理解（Tensor Comprehensions）就基于类似einsum的领域特定语言。此外，可以使用opt einsum和tf einsum opt这样的项目优化einsum表达式的构造顺序。

比方说，我们想要将两个矩阵A ∈ ℝI × K和B ∈ ℝK × J相乘，接着计算每列的和，最终得到向量c ∈ ℝJ。使用爱因斯坦求和约定，这可以表达为：

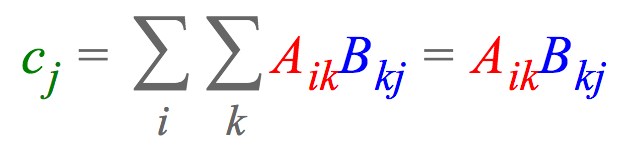
这一表达式指明了c中的每个元素ci是如何计算的，列向量Ai:乘以行向量B:j，然后求和。注意，在爱因斯坦求和约定中，我们省略了求和符号Sigma，因为我们隐式地累加重复的下标（这里是k）和输出中未指明的下标（这里是i）。当然，einsum也能表达更基本的运算。比如，计算两个向量a, b ∈ ℝJ的点积可以表达为：

在深度学习中，我经常碰到的一个问题是，变换高阶张量到向量。例如，我可能有一个张量，其中包含一个batch中的N个训练样本，每个样本是一个长度为T的K维词向量序列，我想把词向量投影到一个不同的维度Q。如果将这个张量记作T ∈ ℝN × T × K，将投影矩阵记作W ∈ ℝK × Q，那么所需计算可以用einsum表达为：

最后一个例子，比方说有一个四阶张量T ∈ ℝN × T × K × M，我们想要使用之前的投影矩阵将第三维投影至Q维，并累加第二维，然后转置结果中的第一维和最后一维，最终得到张量C ∈ ℝM × Q × N。einsum可以非常简洁地表达这一切：

注意，我们通过交换下标n和m（Cmqn而不是Cnqm），转置了张量构造结果。

2. Numpy、PyTorch、TensorFlow中的einsum

einsum在numpy中实现为np.einsum，在PyTorch中实现为torch.einsum，在TensorFlow中实现为tf.einsum，均使用一致的签名einsum(equation, operands)，其中equation是表示爱因斯坦求和约定的字符串，而operands则是张量序列（在numpy和TensorFlow中是变长参数列表，而在PyTorch中是列表）。例如，我们的第一个例子，cj= ∑i∑kAikBkj写成equation字符串就是ik,kj -> j。注意这里(i, j, k)的命名是任意的，但需要一致。

PyTorch和TensorFlow像numpy支持einsum的好处之一是einsum可以用于神经网络架构的任意计算图，并且可以反向传播。典型的einsum调用格式如下：

上式中◻是占位符，表示张量维度。上面的例子中，arg1和arg3是矩阵，arg2是二阶张量，这一einsum运算的结果（result）是矩阵。注意einsum处理的是可变数量的输入。在上面的例子中，einsum指定了三个参数之上的操作，但它同样可以用在牵涉一个参数、两个参数、三个以上参数的操作上。学习einsum的最佳途径是通过学习一些例子，所以下面我们将展示一下，在许多深度学习模型中常用的库函数，用einsum该如何表达（以PyTorch为例）。

2.1 矩阵转置

import torch

a = torch.arange(6).reshape(2, 3)

torch.einsum('ij->ji', [a])

tensor([[ 0., 3.],

[ 1., 4.],

[ 2., 5.]])

2.2 求和

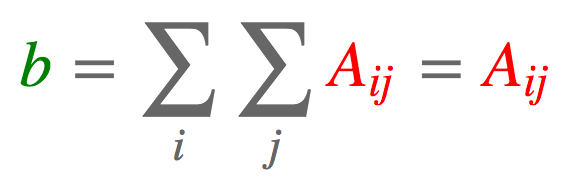
a = torch.arange(6).reshape(2, 3)

torch.einsum('ij->', [a])

tensor(15.)

2.3 列求和

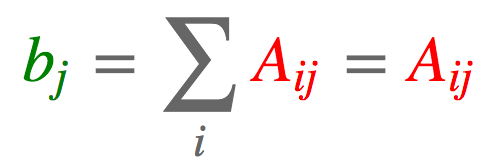
a = torch.arange(6).reshape(2, 3)

torch.einsum('ij->j', [a])

tensor([ 3., 5., 7.])

2.4 行求和

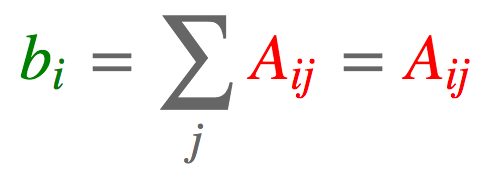
a = torch.arange(6).reshape(2, 3)

torch.einsum('ij->i', [a])

tensor([ 3., 12.])

2.5 矩阵-向量相乘

a = torch.arange(6).reshape(2, 3)

b = torch.arange(3)

torch.einsum('ik,k->i', [a, b])

tensor([ 5., 14.])

2.6 矩阵-矩阵相乘

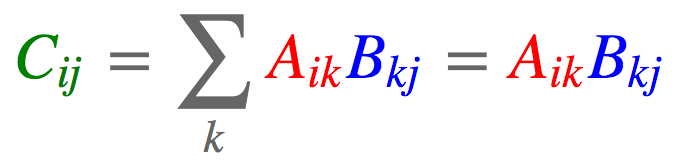
a = torch.arange(6).reshape(2, 3)

b = torch.arange(15).reshape(3, 5)

torch.einsum('ik,kj->ij', [a, b])

tensor([[ 25., 28., 31., 34., 37.],

[ 70., 82., 94., 106., 118.]])

2.7 点积

向量：

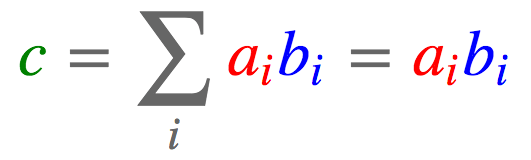
a = torch.arange(3)

b = torch.arange(3,6) # [3, 4, 5]

torch.einsum('i,i->', [a, b])

tensor(14.)

矩阵：

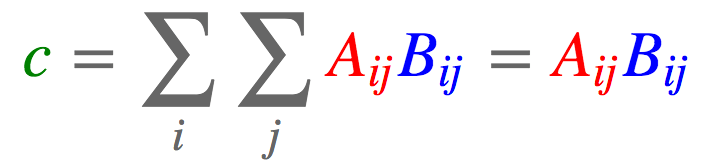
a = torch.arange(6).reshape(2, 3)

b = torch.arange(6,12).reshape(2, 3)

torch.einsum('ij,ij->', [a, b])

tensor(145.)

2.8 哈达玛积

a = torch.arange(6).reshape(2, 3)

b = torch.arange(6,12).reshape(2, 3)

torch.einsum('ij,ij->ij', [a, b])

tensor([[ 0., 7., 16.],

[ 27., 40., 55.]])

2.9 外积

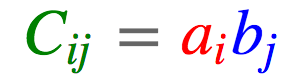
a = torch.arange(3)

b = torch.arange(3,7)

torch.einsum('i,j->ij', [a, b])

tensor([[ 0., 0., 0., 0.],

[ 3., 4., 5., 6.],

[ 6., 8., 10., 12.]])

2.10 batch矩阵相乘

a = torch.randn(3,2,5)

b = torch.randn(3,5,3)

torch.einsum('ijk,ikl->ijl', [a, b])

tensor([[[ 1.0886, 0.0214, 1.0690],

[ 2.0626, 3.2655, -0.1465]],

[[-6.9294, 0.7499, 1.2976],

[ 4.2226, -4.5774, -4.8947]],

[[-2.4289, -0.7804, 5.1385],

[ 0.8003, 2.9425, 1.7338]]])

2.11 张量缩约

batch矩阵相乘是张量缩约的一个特例。比方说，我们有两个张量，一个n阶张量A ∈ ℝI1× ⋯ × In，一个m阶张量B ∈ ℝJ1× ⋯ × Jm。举例来说，我们取n = 4，m = 5，并假定I2= J3且I3= J5。我们可以将这两个张量在这两个维度上相乘（A张量的第2、3维度，B张量的3、5维度），最终得到一个新张量C ∈ ℝI1× I4× J1× J2× J4，如下所示：

a = torch.randn(2,3,5,7)

b = torch.randn(11,13,3,17,5)

torch.einsum('pqrs,tuqvr->pstuv', [a, b]).shape

torch.Size([2, 7, 11, 13, 17])

2.12 双线性变换

如前所述，einsum可用于超过两个张量的计算。这里举一个这方面的例子，双线性变换。

a = torch.randn(2,3)

b = torch.randn(5,3,7)

c = torch.randn(2,7)

torch.einsum('ik,jkl,il->ij', [a, b, c])

tensor([[ 3.8471, 4.7059, -3.0674, -3.2075, -5.2435],

[-3.5961, -5.2622, -4.1195, 5.5899, 0.4632]])

3. 案例

3.1 TreeQN

我曾经在实现TreeQN（ arXiv:1710.11417）的等式6时使用了einsum：给定网络层l上的低维状态表示zl，和激活a上的转换函数Wa，我们想要计算残差链接的下一层状态表示。

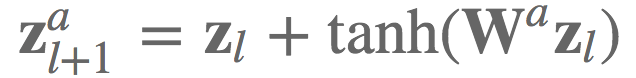
在实践中，我们想要高效地计算大小为B的batch中的K维状态表示Z ∈ ℝB × K，并同时计算所有转换函数（即，所有激活A）。我们可以将这些转换函数安排为一个张量W ∈ ℝA × K × K，并使用einsum高效地计算下一层状态表示。

import torch.nn.functional as F

def random_tensors(shape, num=1, requires_grad=False):

tensors = [torch.randn(shape, requires_grad=requires_grad) for i in range(0, num)]

return tensors[0] if num == 1else tensors

# 参数

# -- [激活数 x 隐藏层维度]

b = random_tensors([5, 3], requires_grad=True)

# -- [激活数 x 隐藏层维度 x 隐藏层维度]

W = random_tensors([5, 3, 3], requires_grad=True)

def transition(zl):

# -- [batch大小 x 激活数 x 隐藏层维度]

return zl.unsqueeze(1) + F.tanh(torch.einsum("bk,aki->bai", [zl, W]) + b)

# 随机取样仿造输入

# -- [batch大小 x 隐藏层维度]

zl = random_tensors([2, 3])

transition(zl)

3.2 注意力

让我们再看一个使用einsum的真实例子，实现注意力机制的等式11-13（arXiv:1509.06664）：

用传统写法实现这些可要费不少力气，特别是考虑batch实现。einsum是我们的救星！

# 参数

# -- [隐藏层维度]

bM, br, w = random_tensors([7], num=3, requires_grad=True)

# -- [隐藏层维度 x 隐藏层维度]

WY, Wh, Wr, Wt = random_tensors([7, 7], num=4, requires_grad=True)

# 注意力机制的单次应用

def attention(Y, ht, rt1):

# -- [batch大小 x 隐藏层维度]

tmp = torch.einsum("ik,kl->il", [ht, Wh]) + torch.einsum("ik,kl->il", [rt1, Wr])

Mt = F.tanh(torch.einsum("ijk,kl->ijl", [Y, WY]) + tmp.unsqueeze(1).expand_as(Y) + bM)

# -- [batch大小 x 序列长度]

at = F.softmax(torch.einsum("ijk,k->ij", [Mt, w]))

# -- [batch大小 x 隐藏层维度]

rt = torch.einsum("ijk,ij->ik", [Y, at]) + F.tanh(torch.einsum("ij,jk->ik", [rt1, Wt]) + br)

# -- [batch大小 x 隐藏层维度], [batch大小 x 序列维度]

return rt, at

# 取样仿造输入

# -- [batch大小 x 序列长度 x 隐藏层维度]

Y = random_tensors([3, 5, 7])

# -- [batch大小 x 隐藏层维度]

ht, rt1 = random_tensors([3, 7], num=2)

rt, at = attention(Y, ht, rt1)

4. 总结

einsum是一个函数走天下，是处理各种张量操作的瑞士军刀。话虽如此，“einsum满足你一切需要”显然夸大其词了。从上面的真实用例可以看到，我们仍然需要在einsum之外应用非线性和构造额外维度（unsqueeze）。类似地，分割、连接、索引张量仍然需要应用其他库函数。

使用einsum的麻烦之处是你需要手动实例化参数，操心它们的初始化，并在模型中注册这些参数。不过我仍然强烈建议你在实现模型时，考虑下有哪些情况适合使用einsum.