频率细化是70年代发展起来的一种新威廉希尔官方网站 ,其主要目的是识别谱图上的细微结构。从通常的FFT分析方法中我们已经知道,在频谱图上的有效频率分布范围是从0HZ到奈魁斯特频率fN为止,而谱线间隔(fs/N)决定了频率分辨能力,N表示数据点数,这里fs表示采样频率,且fN=fs/2。因此,要获得较高的分辨率可从下面两个方面进行。第一方面:降低采样频率,谱线间隔减小,但这样会降低奈魁斯特频率fN,从而导致频率分析范围小;第二方面:提高FFT计算长度N值,但这样要求较大的内存和降低运算速度。
1 频率细化过程介绍
细化威廉希尔官方网站 是一种一定频率范围内提高频率分辨率的测量威廉希尔官方网站 ,也叫细化傅里叶分析。而频率细化是在信号处理和模态分析中广泛应用的一种威廉希尔官方网站 ,它能够提高频率的分辨率,将选定的频率域上的特性曲线放大,从而使系统的频率特性能更清楚地显示出来,如图1所示。
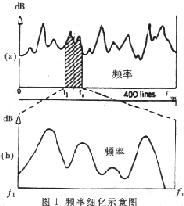
设系统的采样频率为fs,采样点数为NO,则频率分辨率为:
Δf=fs/NO
从上式可以看出,要进行频率细化,即提高频率分辨率,使Δf变小,有两种方法:增加采样点数NO和降低采样频率fs,这里只介绍降低采样频率的方法。
这种方法主要是基于移频原理,如图2所示。

设想要移频部分的频率为fp,其角频率为wp=2πfp,令f (t)=exp(-jwpt)。时域信号x(t)与f(t)卷积后,则在频域上,该信号的fp频率就移到了原点处。
信号频率移到低频后,经过低通滤波,就可以用低的采样频率进行采样,从而达到提高频率分辨率、频率细化的目的。具体过程如图3所示。
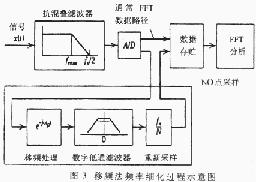
2 移频法频率细化过程中几个问题的分析
(1)非细化处理的系统采样频率为fs,采样点数为NO。对于细化过程,设频率细化倍数为Nr,信号经过抗混叠滤波器后进行A/D采样,采样频率应仍为原来的fs,保持不变,采样点数则为Nr*NO,这样就保证了细化与非细化处理的基本频带范围保持不变,并且可以细化这一频带中的任何一段。
(2)要细化的频率范围为fl~fu,移频后,低频点fl移到原点,则高频点变为(fu-fl)。这时数字低通滤波器的截止频率应大于(fu-fl),并小于低频重采样频率fs/Nr的一半。即截止频率的范围为:
(fu-fl)<fc<fs/2Nr
且可以得到最大细化倍数N与细化频率范围之间的关系为:
Nr<fs/2(fu-fl)
这为设置细化倍数范围提供了依据。
(3)数字低通滤波器的通带必须平,通带内波动要小,这样原信号的频率特性细化后在幅值上才不会改变;同时,最好使滤波器的带外衰减>-70dB,且-70dB处的频率<fs/2Nr,这样就能保证低频重新采样时抗混叠的效果最好。
(4)细化与不细化过程占用时间的比较:由于采样点数NO保持不变,因此细化处理的FFT时间与不细化的FFT时间一样,都是 NOLog(NO)/2;细化过程要进行Nr*NO点的高频采样和NO点的低频采样,而不细化过程只进行NO点的高频采样,所以在采样时间上,细化过程要稍长一点。
(5)移频法频率细化与增加采样点数频率细化的比较:移频法频率细化只进行NO个点的FFT变换,和一些数组、矩阵的运算,它所花的时间约为:NOLog(NO)/2;而采用增加采样点数频率细化要进行Nr*NO个点的FFT变换,它所花的时间约为:(Nr*NO)Log(Nr*No) /2。
移频是将感兴趣的频段的下限频率移至原来的零频率位置,以便有可能将感兴趣频段放大到整个频率显示范围上,需首先对信号进行频率调制。这里采用的是复数调制法,如果欲将某一频率fo移至原来的零频处,则以原信号x1与 exp(-j2pi*f0*k*?t) 相调制得:实部为 x1cos((2*pi*f0*k)/(N*?f)),虚部为-x1sin((2*pi*f0*k)/(N*?f))。若令L0=f0/?f(?f---原有的频率分辨率),即为频率在原频谱图中所对应的谱线序号,则实部和虚部即可以写为: x1cos(2*pi/N*L0*k)及 -x1sin(2*pi/N*L0*k),合并实部和虚部可以得到调制后的信号为 wn=exp(-j*2pi/N),
由于移频使fl前面的频段移到频域的负轴上,而低通滤波又滤掉了fu后面的高频部分,因此,这种方法只能进行一段频率的细化,不能进行全频段的细化,这是移频法频率细化的缺点。要进行全频段细化,可以采用增加采样点数的方法。
用MATLAB程序仿真图3这个过程,主要实现A/D采样、移频、低通滤波、低频重新采样、FFT变换等,同时注意上面几个问题的分析。
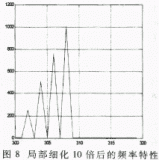
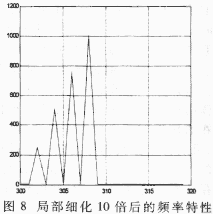
总信号由302Hz、304Hz、306Hz、308Hz四个不同频率、不同幅值的正余弦信号合成。采样点为512,采样频率为5120Hz,则频率分辨率为10Hz,这在频域内分辨不出这四个信号。仿真软件在300~320Hz范围内细化10倍,则这时频率分辨率为1Hz,就可以逐渐看清楚这四个信号。
x(t)=sin(2*302)+2cos(2π*304)+3sin(2π*306)+4sin(2π*308)
细化处理需要5120个采样点,仿真时A/D采样用对连续信号x(t)进行离散化来代替,离散化的点值就是采样值,它们组成一个数组(矩阵),这是一个点序列。
采样完成后,对采样点进行移频仿真(将300Hz移频到原点),由以下步骤实现:
令:F1=300W1=2π*F1
f(t)=exp(-jw1*t)
t取离散化时刻,Δt=1/fsTk=k*Δt
则f(t)离散化可变为:
f(k)=exp(-jw1*Tk)
=exp[(-j2π*f1*k)/fs]
这也是一个点序列。
MATLAB将上面两个点序列进行卷积(矩阵相乘),得到一个新的点序列,就实现了移频过程,即使F1=300Hz 在频域上移动了0,其它频率特性依此前移。
MATLAB语言有很方便的滤波器设计和数字滤波功能,可用它设计一个带内波动<0.1dB,带外衰减>-70dB,截止频率为20Hz的低通滤波器,并将上面的点序列进行数字滤波,得到一个只在0~20Hz频段上有特性曲线、其它频段被滤掉的信号的点序列。
对上面的点序列每隔10点(细化倍数)进行抽取,实际上就是对经移频、滤波后的信号进行重新采样。采样频率为S120Hz/10,即采样频率降低了10倍,抽取得到512个点。
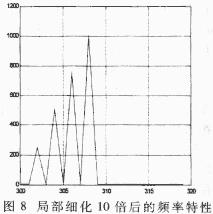
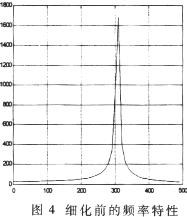
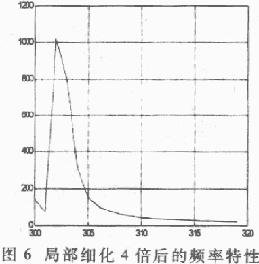
对这512个点进行FFT变换,就可以得到300Hz~320Hz频段上已细化10倍的频率特性曲线了,结果如图4、图8所示。
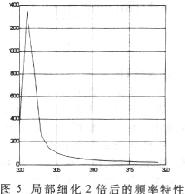
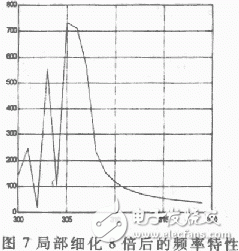
用仿真程序分别进行2、4、8、10倍的频率细化,从运行结果可以看出,细化倍数越大,频率分辨率就越高,频域波形越看得清楚,这与理论是相符合的。
-
滤波器
+关注
关注
161文章
7837浏览量
178305 -
仿真
+关注
关注
50文章
4095浏览量
133697 -
分辨率
+关注
关注
2文章
1067浏览量
41959
发布评论请先 登录
相关推荐
基于傅里叶变换(DSTFT)的移频键控(FSK)信号的解调
无线电波传输:多普勒频移
方波移相电路,移想过程中方波有点失真?
主动移频法在光伏并网逆变器并联运行下的孤岛检测机理研究
微波器件薄膜化过程中的威廉希尔官方网站 难点分析
基于MATLAB仿真频率细化过程介绍




 移频法频率细化的优势及在过程中遇到的问题解析
移频法频率细化的优势及在过程中遇到的问题解析










评论