卡尔曼滤波(Kalman filter)是一种高效的自回归滤波器,它能在存在诸多不确定性情况的组合信息中估计动态系统的状态,是一种强大的、通用性极强的工具。它的提出者,鲁道夫.E.卡尔曼,在一次访问NASA埃姆斯研究中心时,发现这种方法能帮助解决阿波罗计划的轨道预测问题,后来NASA在阿波罗飞船的导航系统中确实也用到了这个滤波器。最终,飞船正确驶向月球,完成了人类历史上的第一次登月。
本文是国外博主Bzarg在2015年写的一篇图解。虽然是几年前的文章,但是动态定位、自动导航、时间序列模型、卫星导航——卡尔曼滤波的应用范围依然非常广。那么,作为软件工程师和机器学习工程师,你真的了解卡尔曼滤波吗?
什么是卡尔曼滤波?
对于这个滤波器,我们几乎可以下这么一个定论:只要是存在不确定信息的动态系统,卡尔曼滤波就可以对系统下一步要做什么做出有根据的推测。即便有噪声信息干扰,卡尔曼滤波通常也能很好的弄清楚究竟发生了什么,找出现象间不易察觉的相关性。
因此卡尔曼滤波非常适合不断变化的系统,它的优点还有内存占用较小(只需保留前一个状态)、速度快,是实时问题和嵌入式系统的理想选择。
如果你曾经Google过卡尔曼滤波的教程(如今有一点点改善),你会发现相关的算法教程非常可怕,而且也没具体说清楚是什么。事实上,卡尔曼滤波很简单,如果我们以正确的方式看它,理解是很水到渠成的事。
本文会用大量清晰、美观的图片和颜色来解释这个概念,读者只需具备概率论和矩阵的一般基础知识。
我们能用卡尔曼滤波做什么?
让我们举个例子:你造了一个可以在树林里四处溜达的小机器人,为了让它实现导航,机器人需要知道自己所处的位置。
也就是说,机器人有一个包含位置信息和速度信息的状态xk:
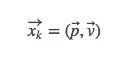
注意,在这个例子中,状态是位置和速度,放进其他问题里,它也可以是水箱里的液体体积、汽车引擎温度、触摸板上指尖的位置,或者其他任何数据。
我们的小机器人装有GPS传感器,定位精度10米。虽然一般来说这点精度够用了,但我们希望它的定位误差能再小点,毕竟树林里到处都是土坑和陡坡,如果机器人稍稍偏了那么几米,它就有可能滚落山坡。所以GPS提供的信息还不够充分。
我们也可以预测机器人是怎么移动的:它会把指令发送给控制轮子的马达,如果这一刻它始终朝一个方向前进,没有遇到任何障碍物,那么下一刻它可能会继续坚持这个路线。但是机器人对自己的状态不是全知的:它可能会逆风行驶,轮子打滑,滚落颠簸地形……所以车轮转动次数并不能完全代表实际行驶距离,基于这个距离的预测也不完美。
这个问题下,GPS为我们提供了一些关于状态的信息,但那是间接的、不准确的;我们的预测提供了关于机器人轨迹的信息,但那也是间接的、不准确的。
但以上就是我们能够获得的全部信息,在它们的基础上,我们是否能给出一个完整预测,让它的准确度比机器人搜集的单次预测汇总更高?用了卡尔曼滤波,这个问题可以迎刃而解。
卡尔曼滤波眼里的机器人问题
还是上面这个问题,我们有一个状态,它和速度、位置有关:
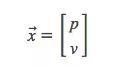
我们不知道它们的实际值是多少,但掌握着一些速度和位置的可能组合,其中某些组合的可能性更高:
卡尔曼滤波假设两个变量(在我们的例子里是位置和速度)都应该是随机的,而且符合高斯分布。每个变量都有一个均值μ,它是随机分布的中心;有一个方差σ2,它衡量组合的不确定性。
在上图中,位置和速度是不相关的,这意味着我们不能从一个变量推测另一个变量。
那么如果位置和速度相关呢?如下图所示,机器人前往特定位置的可能性取决于它拥有的速度。
这不难理解,如果基于旧位置估计新位置,我们会产生这两个结论:如果速度很快,机器人可能移动得更远,所以得到的位置会更远;如果速度很慢,机器人就走不了那么远。
这种关系对目标跟踪来说非常重要,因为它提供了更多信息:一个可以衡量可能性的标准。这就是卡尔曼滤波的目标:从不确定信息中挤出尽可能多的信息!
为了捕获这种相关性,我们用的是协方差矩阵。简而言之,矩阵的每个值是第i个变量和第j个变量之间的相关程度(由于矩阵是对称的,i和j的位置可以随便交换)。我们用Σ表示协方差矩阵,在这个例子中,就是Σij。
用矩阵描述问题
为了把以上关于状态的信息建模为高斯分布(图中色块),我们还需要k时的两个信息:最佳估计x̂k(均值,也就是μ),协方差矩阵Pk。(虽然还是用了位置和速度两个变量,但只要和问题相关,卡尔曼滤波可以包含任意数量的变量)

接下来,我们要通过查看当前状态(k-1时)来预测下一个状态(k时)。这里我们查看的状态不是真值,但预测函数无视真假,可以给出新分布:
我们可以用矩阵Fk表示这个预测步骤:
它从原始预测中取每一点,并将其移动到新的预测位置。如果原始预测是正确的,系统就会移动到新位置。
这是怎么做到的?为什么我们可以用矩阵来预测机器人下一刻的位置和速度?下面是个简单公式:
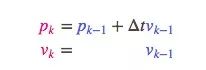
换成矩阵形式:
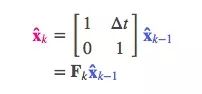
这是一个预测矩阵,它能给出机器人的下一个状态,但目前我们还不知道协方差矩阵的更新方法。这也是我们要引出下面这个等式的原因:如果我们将分布中的每个点乘以矩阵A,那么它的协方差矩阵会发生什么变化?
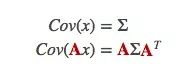
把这个式子和上面的最佳估计x̂k结合,可得:
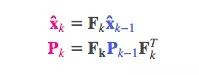
外部影响
但是,除了速度和位置,外因也会对系统造成影响。比如interwetten与威廉的赔率体系 火车运动,除了列车自驾系统,列车操作员可能会手动调速。在我们的机器人示例中,导航软件也可以发出停止指令。对于这些信息,我们把它作为一个向量uk,纳入预测系统作为修正。
假设油门设置和控制命令是已知的,我们知道火车的预期加速度a。根据运动学基本定理,我们可得:

把它转成矩阵形式:

Bk是控制矩阵,uk是控制向量。如果外部环境异常简单,我们可以忽略这部分内容,但是如果添加了外部影响后,模型的准确率还是上不去,这又是为什么呢?
外部不确定性
当一个国家只按照自己的步子发展时,它会自生自灭。当一个国家开始依赖外部力量发展时,只要这些外部力量是已知的,我们也能预测它的存亡。
但是,如果存在我们不知道的力量呢?当我们监控无人机时,它可能会受到风的影响;当我们跟踪轮式机器人时,它的轮胎可能会打滑,或者粗糙地面会降低它的移速。这些因素是难以掌握的,如果出现其中的任意一种情况,预测结果就难以保障。
这要求我们在每个预测步骤后再加上一些新的不确定性,来模拟和“世界”相关的所有不确定性:
如上图所示,加上外部不确定性后, x̂k−1的每个预测状态都可能会移动到另一点,也就是蓝色的高斯分布会移动到紫色高斯分布的位置,并且具有协方差Qk。换句话说,我们把这些不确定影响视为协方差Qk的噪声。
这个紫色的高斯分布拥有和原分布相同的均值,但协方差不同。
我们在原式上加入Qk:
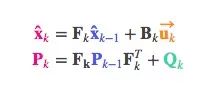
简而言之,这里“新的最佳估计=原最佳估计+已知外部影响”,“新的不确定性预测=原预测+外部环境的不确定性”。
现在,有了这些概念介绍,我们可以把传感器数据输入其中。
通过测量来细化估计值
我们可能有好几个传感器,它们一起提供有关系统状态的信息。传感器的作用不是我们关心的重点,它可以读取位置,可以读取速度,重点是,它能告诉我们关于状态的间接信息——它是状态下产生的一组读数。
请注意,读数的规模和状态的规模不一定相同,所以我们把传感器读数矩阵设为Hk。
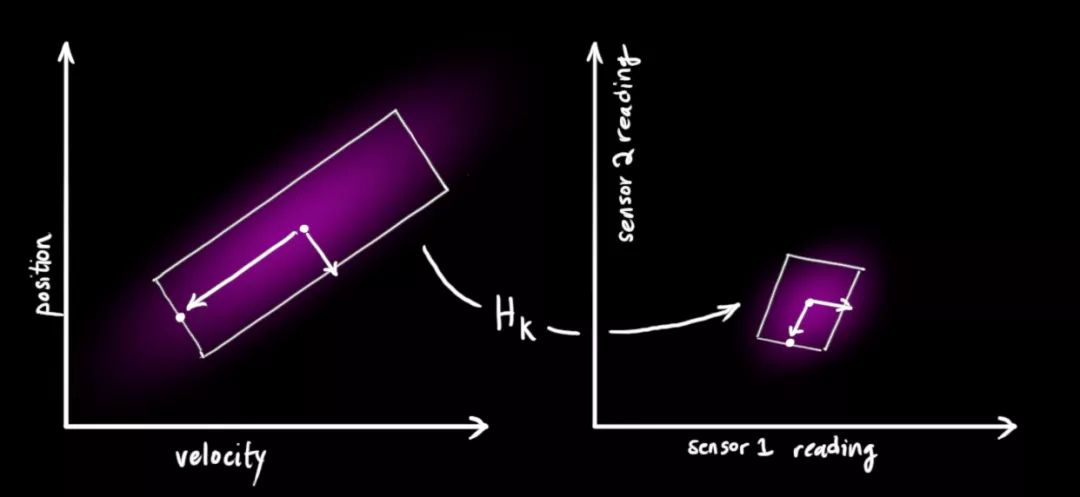
把这些分布转换为一般形式:
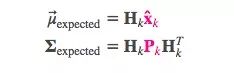
卡尔曼滤波的一大优点是擅长处理传感器噪声。换句话说,由于种种因素,传感器记录的信息其实是不准的,一个状态事实上可以产生多种读数。

我们将这种不确定性(即传感器噪声)的协方差设为Rk,读数的分布均值是zk。
现在我们得到了两块高斯分布,一块围绕预测的均值,另一块围绕传感器读数。
如果要生成靠谱预测,模型必须调和这两个信息。也就是说,对于任何可能的读数(z1,z2),这两种方法预测的状态都有可能是准的,也都有可能是不准的。重点是我们怎么找到这两个准确率。
最简单的方法是两者相乘:
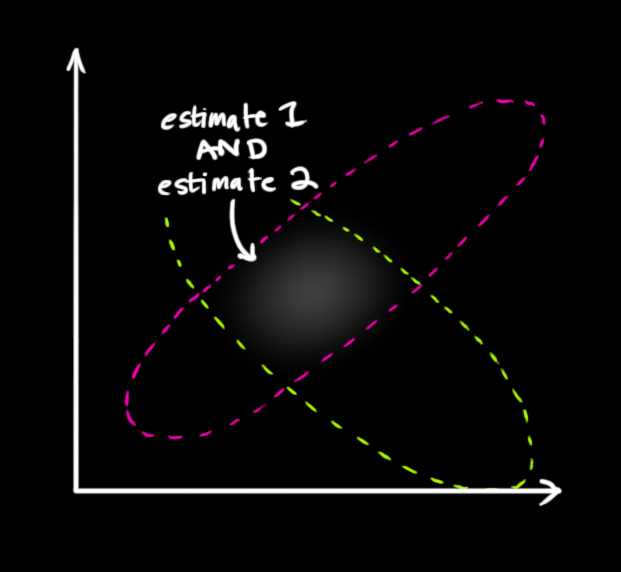
两块高斯分布相乘后,我们可以得到它们的重叠部分,这也是会出现最佳估计的区域。换个角度看,它看起来也符合高斯分布:
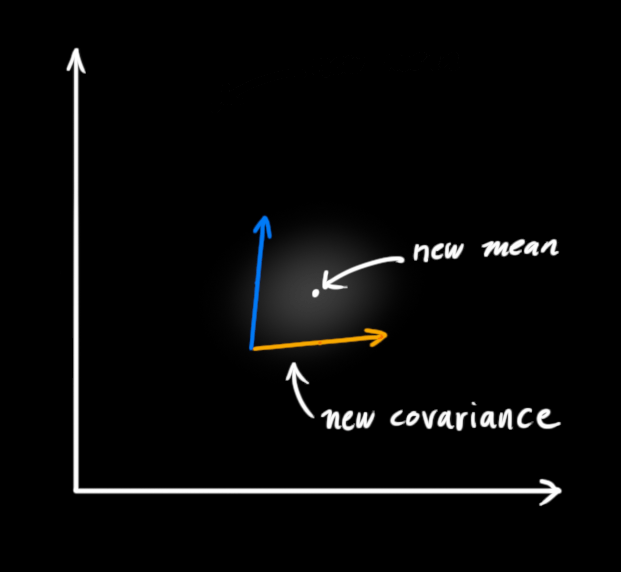
事实证明,当你把两个高斯分布和它们各自的均值和协方差矩阵相乘时,你会得到一个拥有独立均值和协方差矩阵的新高斯分布。最后剩下的问题就不难解决了:我们必须有一个公式来从旧的参数中获取这些新参数!
结合高斯
让我们从一维看起,设方差为σ2,均值为μ,一个标准一维高斯钟形曲线方程如下所示:

那么两条高斯曲线相乘呢?

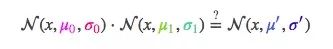
把这个式子按照一维方程进行扩展,可得:
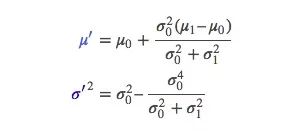
如果有些太复杂,我们用k简化一下:

还记得之前我们算不确定性的时候多麻烦吗?这里结合高斯算多简单!以上是一维的内容,如果是多维空间,把这个式子转成矩阵格式:

这个矩阵K就是我们说的卡尔曼增益,easy!
把它们结合在一起
截至目前,我们有用矩阵 (μ0,Σ0)=(Hkx̂k,HkPkHTk)预测的分布,有用传感器读数 (μ1,Σ1)=(zk,Rk)预测的分布。把它们代入上节的矩阵等式中:
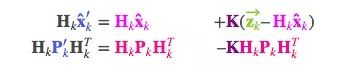
相应的,卡尔曼增益就是:

考虑到K里还包含着一个Hk,我们再精简一下上述等式:

最后,x̂k′是我们的最佳估计值,我们可以把它继续放进去做另一轮预测:
-
机器人
+关注
关注
211文章
28390浏览量
206949 -
卡尔曼滤波
+关注
关注
3文章
165浏览量
24648
原文标题:图说卡尔曼滤波:阿波罗登月飞船背后的秘密
文章出处:【微信号:jqr_AI,微信公众号:论智】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
卡尔曼滤波器是什么
卡尔曼滤波的变种有哪些?1
卡尔曼滤波的变种有哪些?2
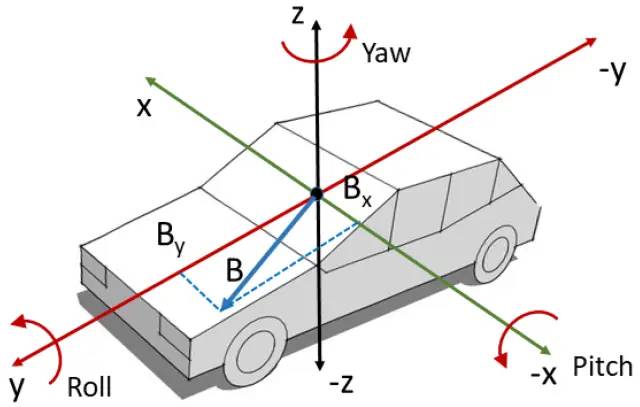
卡尔曼滤波的变种有哪些?3
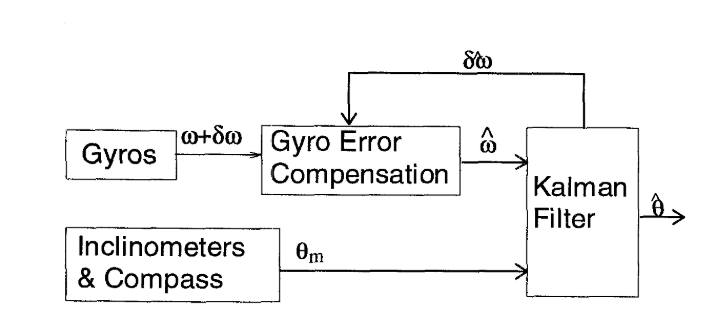
卡尔曼滤波的变种有哪些?4
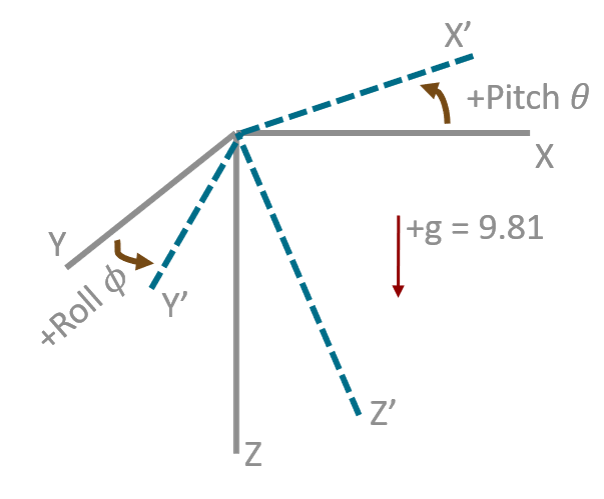




 什么是卡尔曼滤波? 浅谈卡尔曼滤波眼里的机器人问题
什么是卡尔曼滤波? 浅谈卡尔曼滤波眼里的机器人问题
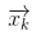
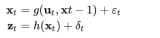










评论