区块链威廉希尔官方网站 浅析：交易脚本中的椭圆曲线加密算法

一、重新审视RSA

RSA之所以能作为非对称加密算法，其实有两点：

1. 基于大整数质数分解这个数学难题。这个难题，求解出来很困难，但是验证它很简单

2. 私钥签名之后，利用公钥进行验证的还原公式，RSA里面就是欧拉定理。

在比特币中，非对称加密使用的数学难题是离散对数问题。

二、椭圆曲线算法的数学难题

在阅读本节之前，可以先阅读ECC加密算法入门介绍，什么是椭圆曲线呢，并不是我们高中所学的在连续实数域二维平面上的椭圆曲线，而是定义在有限域(有限个离散的值组成的集合)射影平面上的曲线。

先不考虑有限域和射影平面，假设还是在连续实数域二维平面上，就像二维平面上其他曲线都有方程一样，椭圆曲线的方程是：

y2+ a1xy + a3y = x3+ a2x2+ a4x + a6

且曲线上的每个点都是非奇异（或光滑）的，也就是都有切线。

(下面都只讨论实数域和二维平面上的情况，理解了这部分，剩下的仅仅是扩展的问题，非常容易理解)

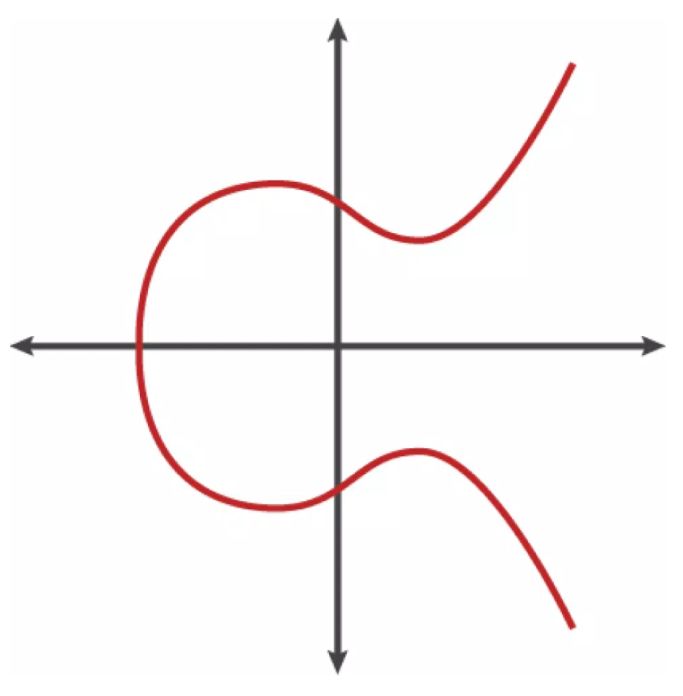
根据参数不同，曲线形状不同，比如

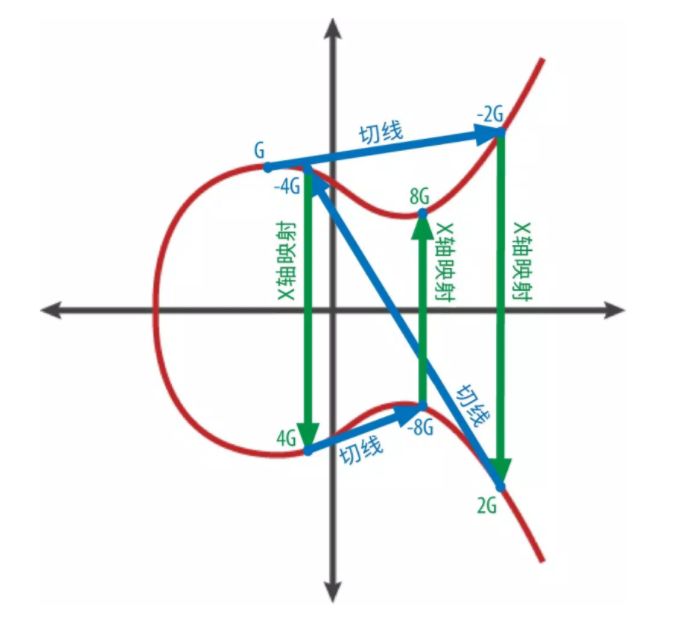
在这条曲线上定义了加法：就像上图，先定义一点G，然后过G做该椭圆曲线的切线，和椭圆曲线相交于另外一点，称为点-2G，找到点-2G关于X轴的点2G，该点在椭圆曲线上，因为比特币选定的椭圆曲线是关于X轴对称的。(根据参数不同，有很多椭圆曲线，有些不关于X轴对称，有一些关于X轴对称，比特币选定的关于X轴对称的曲线叫secp256k1)。点2G称为点G + 点G的加法。如果G做k次加法，也就是 点2G + 点G = 点3G，点3G + 点G = 点4G，一直加k次，得到点kG。

那么数学难题是什么呢？数学难题是：已知k和G，得出K = kG，是容易的，有公式直接得出，但是由kG的结果K，和点G，得出k是困难的。你看，这也是一个验证很简单，但是求解很困难的事情。为什么求解很困难？其实是相对于从k和G得出K而言的。首先需要明确的是，一步一步的计算，从k和G能得出K(正向)，从K和G也能得出k(逆向)，时间复杂度也就是O(k)，但是如果正向计算能使用一些方法快速求出来，而这个方法对逆向计算不适用，那么就构成了计算的非对称性。椭圆曲线加密算法正是这样的，正向计算可以使用比如 倍数-和 的方法(如果加法看成是乘法，那么就叫 平方-乘 的方法)，但是逆向计算仍然没有找到合适的快速的方法。该部分可以参见《密码学原理与实践》的第六章。

三、椭圆曲线算法的还原方法的设计

下面只是一个例子，还有很多其他的方法。

1. 加密签名的过程：

A. 选择一条椭圆曲线和基点GB. 选择私有密钥k，利用基点G计算公开密钥K = kGC. 产生一个随机整数r，计算点R = rGD. 将明文m和点R的坐标值x, y作为参数，计算SHA值，即Hash = SHA(m, x, y)E. 计算sn = r – Hash * kF. 将sn和Hash作为密文

2. 对应的验证过程如下

(公开的信息有：基点G，公开密钥K，sn，m和Hash)A. 计算点R(x, y) = sn * G + Hash * K

B. 计算H = SHA(m, x, y)

C. 如果H和Hash值相同，则验证成功。

因为：sn = r – Hash * k则验证公式为：sn * G + Hash * K= (r – Hash * k) * G + Hash * K= r * G – Hash * k * G + Hash * K= r * G – Hash * K + Hash * K= rG = R

(以上计算都是基于模的运算)

其实可以思考一下为啥需要一个随机数r，因为如果没有随机数，那么给出的密文是sn = Hash * k，因为Hash是已知的，所以这样暴露了k * Hash以及k * G，安全性会降低。

四、椭圆曲线算法和RSA的比较

1. 椭圆曲线算法的优点

安全性能更高

160位ECC与1024位RSA、DSA有相同的安全强度

处理速度更快

在私钥的处理速度上，ECC远 比RSA、DSA快得多

带宽要求更低

存储空间更小

ECC的密钥尺寸和系统参数与RSA、DSA相比要小得多

2. 椭圆曲线算法的缺点

设计困难，实现复杂

如果序列号设计过短，那么安全性并没有想象中的完善