关于超前滞后零极点频率补偿器原理及应用

零极点补偿器(Pole-zero compensator)常用于修正反馈放大器回路的幅度和相位。这篇文章超出了教科书标准的解释程度，本文考虑了工程师在使用补偿器设计电路时需要注意的地方，甚至还涉及了补偿器设计所采用晶体管的细节。

无源补偿器

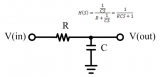
零极点补偿器可以是超前-滞后或滞后-超前补偿器。它们经常出现在电路和控制理论教科书中。最常见的无源电路补偿器有三个器件：两个电阻和一个电容。图1所示的电路放置在放大器内方便的位置，尤其是在反馈回路中，以提供额外的相位或高频幅度“加重”。

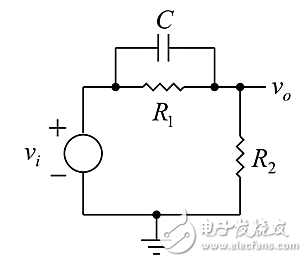
图1：典型的无源电路补偿器。

该电路本质上是个RC分频器，增加了与C并联的电阻R1。R1、C组合的阻抗为：

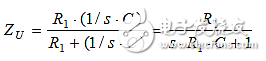
那么，传递函数就是分压器公式：

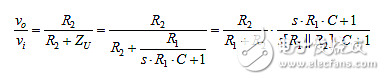
第一个因子是准静态(0 + Hz)增益，即没有C的分压器。动态或频率相关因子在ωz =–1/R1C处有一个零点；在ωp =–1/(R1 || R2)C处有一个极点。

当使用波特(Bode)或频率响应图时，使用频率ω的大小(即其绝对值)，负号被丢弃。

但是，请记住，波特图上的极点和零点频率不是正极点和零点——通常不是，但如果是的话，它们在图示上仍然是正的。

由于并联电阻的阻值比R1低，所以它们也具有较低的时间常数和较高频率。极点频率比零点高。

随着频率从低值开始增加，零点开始在低于ωz约十分之一的地方产生正向(超前)相位，它以45o/dec的线性增加，直到ωz为+ 45°。然后再高十倍，达到+90o；其在ωz的每一侧都有十倍的相位影响。

类似，极点在ωp周围有±10倍的相位相等范围，但在ωp的每一侧以–45o/dec线性地贡献负(滞后)相位。在ωp，极点的相位贡献是–45o。(极点或零点相位线性近似的最大误差约为±6o。)

如果ωp > ωz超过二十倍，则极点与零点之间不存在相位的相互作用，可以实现从零点开始的完整的+ 90°相位。

零点相位超前位于回路增益幅度||GH||=1附近，位于回路的横向或单位增益或交叉频率fT处。

对于||GH||< 1，回路没有足够的反馈幅度(与正弦波幅度相同)来维持振荡。

反馈电路中的常见问题是相位滞后或延迟过大，以及回路周围的相移(回路增益GH)太接近-180°(-π，以弧度表示)。回路中添加补偿器以加大正相位。这增加了相位裕度，即给定频率与-180°(回路振荡处)之间的回路相位差。

因此，一般的反馈设计目标是在fT处将回路相位保持在-180°以上，以实现正相位裕度。

理想情况下，补偿器只应贡献零点而没有极点，但实际的interwetten与威廉的赔率体系 电路总是产生不少于零点的极点。(在系统级，通过并联电路、有方法可以规避这种情况，例如在PID补偿器中。而在柏拉图式的理想DSP世界中，可以无极点地编程零点，但不能实时实现！)

超前-滞后补偿器有一个不需要的极点伴随着所需的零点。使用该电路进行补偿设计的挑战是将零点放置在需要额外(正)相位的位置，同时将极点放置在对回路动态性能无关宏旨的较高频率处，高于fT十倍以上是不错的选择。

为分离极点和零点，必须通过使R2 < < R1来分开时间常数。然而，这也使得分频器准静态增益 < < 1。是利是弊，取决于回路。对于由准静态回路增益太大导致振荡(或循环过度)的回路，GH0不仅会产生零点增加相位，而且由分频器引起的GH0的减小会使波特幅度曲线向下。因幅度随频率下降，fT经由移动到图2中左侧(如图2所示)而降低——下降到相位延迟不那么大且回路更稳定的位置。

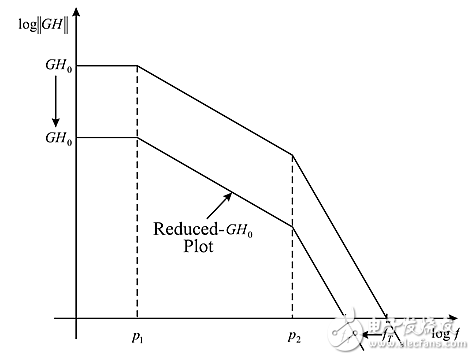
图2：使用补偿器后的波特图变化。

另一方面，如果回路的极点太多，但又必须保持回路增益以满足精度(准静态误差)要求，则超前-滞后补偿器不是合适的补救措施。 零点可以用来消除不需要的极点，但频率更高的补偿器极点仍存在。

实际上，补偿器只是将回路极点转移到更高频率，尽管不超过十倍。 这有时太过微不足道。

因此，当额外的零点和减小的准静态增益都有利于控制时，最好使用超前-滞后补偿器。

双无源和有源补偿器

接着反馈回路的零极点补偿器继续讲，并提出了一些教科书中通常看不到的方法。 双(dual)RC超前-滞后补偿器是RL超前-滞后补偿器，如下所示，其传递函数为：

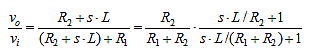
不采用并联-R极点，双重补偿器采用串联-R极点、时间常数τp=L/(R1+R2)；而零点时间常数为τz = L/(R2)。极点的串联-R大于零点的，在时间常数的分母中，极点频率较大：对于RC超前-滞后电路，ωp>ωz。

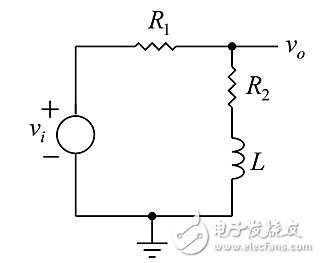
图3：双重补偿器电路图。

用电容来实现电路通常比用电感更合适，但有个有趣的例外：即当电感由晶体管和电阻合成时，如图4所示。

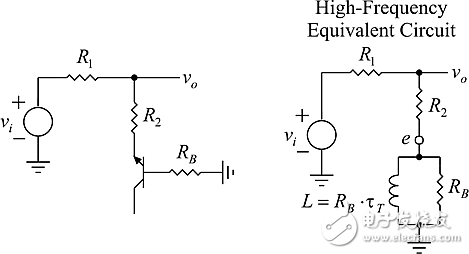
图4：电感由晶体管和电阻合成的补偿器及其高频等效电路。

在fβ(β(s)开始滚降)和fT(β(s)=1)之间，是晶体管的高频(hf)区域，其中基极阻抗在发射极旋转+ 90°。

在该hf区域中的基极电阻RB采用如右侧所示的等效电路(并联RL)，其中电感值取决于BJT的速度(由fT表示)，并在表述L的公式中用作τT，其中τT = 1/ωT = 1/2 x π x fT。

该等效电路可方便地用于在高频区补偿的超前-滞后补偿器。它与L被RB分流的无源版本不同。

当为传递函数求解该hf等效电路时：

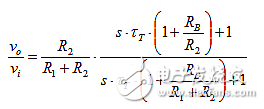
该电路有一个零点和一个极点，极点/零点频率之比为：

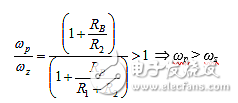
通过R1>>R2分开极点和零点。(接近或在同一频率上的极点和零点是双重点(doublet))。其对准静态增益产生的效果与对无源电路的相同。RB影响极点和零点的位置，并在频率上移动极点和零点。极点和零点被限制在高频区域，或者当回转(gyration)停止在该区域之外时，L“消失”。在fβ以下，仅为RB/(β0+1)。

该主题的一个变化如下所示，采用了并联L、R2，而非串联。

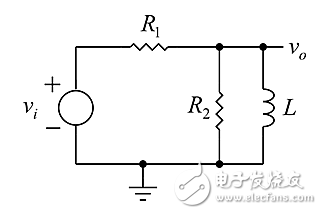
图5：变化后的补偿器电路。

RL超前-滞后补偿器的传递函数为：

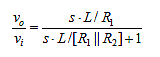
它与RC补偿器在形式上的类似处在于都具有并联-R极点，不同处在于在原点(origin)有零点。零点和极点频率分别为ωz=–1/(L/R1)和ωp=–L/[R1||R2]；其中零点频率是零点增益达到一时的频率。利用了相同的一般考虑。

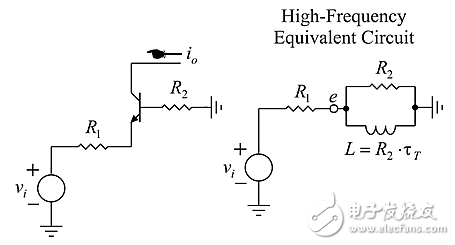
图6：有源补偿器及其高频等效电路。

滞后-超前补偿器通过安置ωp<ωz以降低低频下的回路增益，然后当fT接近以-1双对数斜率穿越fT的平稳过渡时，将幅度响应从零点展开(flare out)。相同的有源器件电感合成可用于合成有源滞后-超前电路。