13种神经网络激活函数

机器学习初创公司Mate Labs联合创始人Kailash Ahirwar简要介绍了13种神经网络激活函数。

激活函数将非线性引入网络，因此激活函数自身也被称为非线性。神经网络是普适的函数逼近器，而深度神经网络基于反向传播训练，因此要求可微激活函数。反向传播在这一函数上应用梯度下降，以更新网络的权重。理解激活函数非常重要，因为它对深度神经网络的质量起着关键的作用。本文将罗列和描述不同的激活函数。

线性激活函数

恒等函数（Identity）或线性激活（Linear activation）函数是最简单的激活函数。输出和输入成比例。线性激活函数的问题在于，它的导数是常数，梯度也是常数，梯度下降无法工作。

值域：(-∞, +∞)

例子：f(2) = 2或f(-4) = -4

阶跃函数

阶跃函数（Heaviside step function）通常只在单层感知器上有用，单层感知器是神经网络的早期形式，可用于分类线性可分的数据。这些函数可用于二元分类任务。其输出为A1（若输入之和高于特定阈值）或A0（若输入之和低于特定阈值）。感知器使用的值为A1 = 1、A0 = 0.

值域：0或1

例子：f(2) = 1、f(-4) = 0、f(0) = 0、f(1) = 1

图片来源：维基百科

sigmoid函数

sigmoid函数，也称逻辑激活函数（Logistic activation function）最常用于二元分类问题。它有梯度消失问题。在一定epoch数目之后，网络拒绝学习，或非常缓慢地学习，因为输入（X）导致输出（Y）中非常小的改动。现在，sigmoid函数主要用于分类问题。这一函数更容易碰到后续层的饱和问题，导致训练变得困难。计算sigmoid函数的导数非常简单。

就神经网络的反向传播过程而言，每层（至少）挤入四分之一的误差。因此，网络越深，越多关于数据的知识将“丢失”。某些输出层的“较大”误差可能不会影响相对较浅的层中的神经元的突触权重（“较浅”意味着接近输入层）。

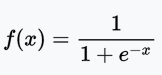
sigmoid函数定义

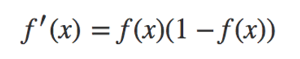
sigmoid函数的导数

值域：(0, 1)

例子：f(4) = 0.982、f(-3) = 0.0474、f(-5) = 0.0067

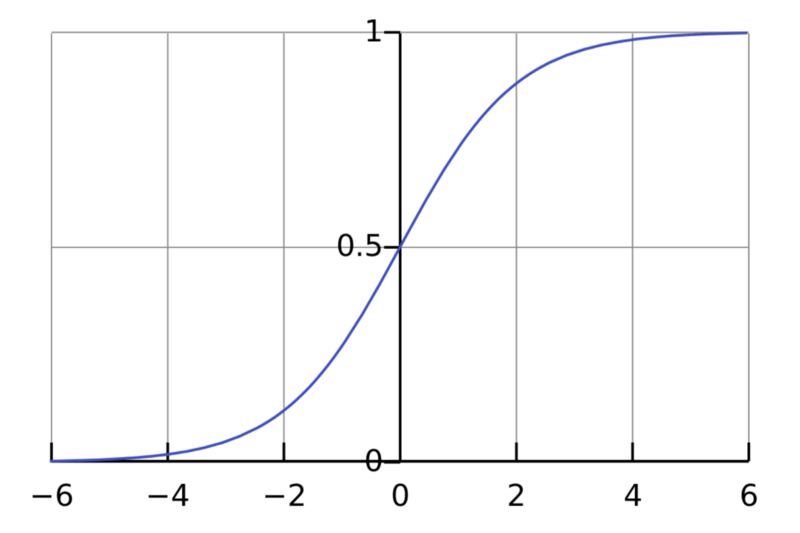
图片来源：维基百科

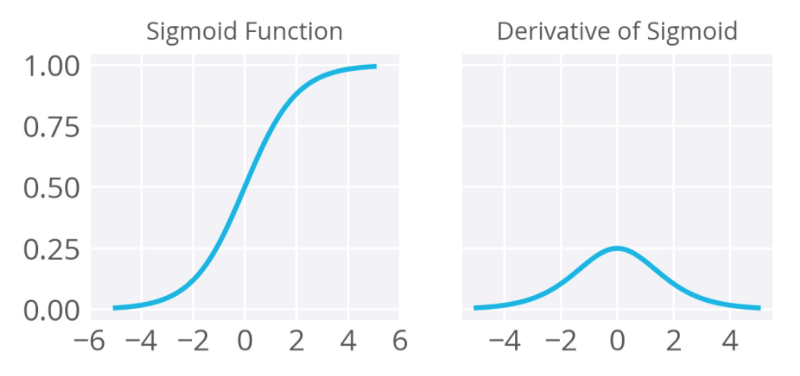
图片来源：deep learning nano foundation

tanh函数

tanh函数是拉伸过的sigmoid函数，以零为中心，因此导数更陡峭。tanh比sigmoid激活函数收敛得更快。

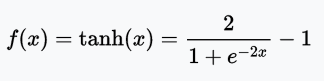
值域：(-1, 1)

例子：tanh(2) = 0.9640、tanh(-0.567) = -0.5131、tanh(0) = 0

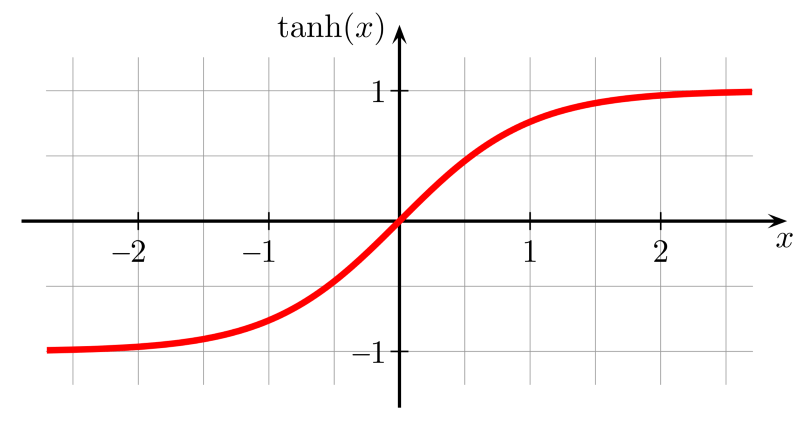
图片来源：维基百科

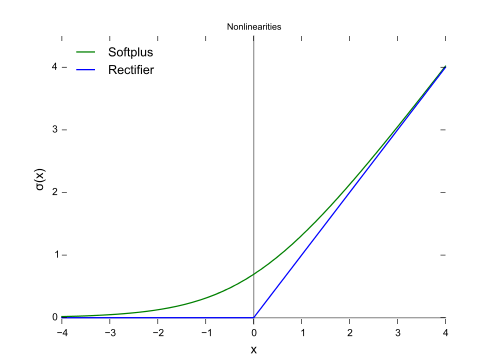
ReLU函数

ReLU（Rectified Linear Unit，修正线性单元）训练速度比tanh快6倍。当输入值小于零时，输出值为零。当输入值大于等于零时，输出值等于输入值。当输入值为正数时，导数为1，因此不会出现sigmoid函数反向传播时的挤压效应。

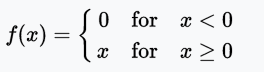
值域：[0, x)

例子：f(-5) = 0、f(0) = 0、f(5) = 5

图片来源：维基百科

不幸的是，ReLU在训练时可能很脆弱，可能“死亡”。例如，通过ReLU神经元的较大梯度可能导致权重更新过头，导致神经元再也不会因为任何数据点激活。如果这一情况发生了，经过这一单元的梯度从此以后将永远为零。也就是说，ReLU单元可能在训练中不可逆地死亡，因为它们被从数据流形上踢出去了。例如，你可能发现，如果学习率设置过高，40%的网络可能“死亡”（即神经元在整个训练数据集上永远不会激活）。设置一个合适的学习率可以缓解这一问题。

-- Andrej Karpathy CS231n 课程

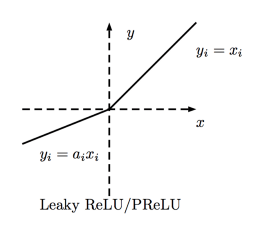
Leaky ReLU函数

Leaky ReLU让单元未激活时能有一个很小的非零梯度。这里，很小的非零梯度是0.01.

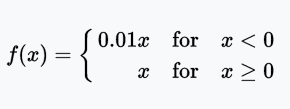
值域：(-∞, +∞)

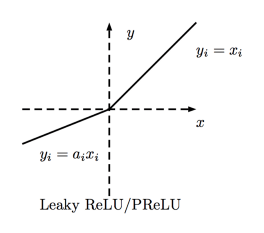
PReLU函数

PReLU（Parametric Rectified Linear Unit）函数类似Leaky ReLU，只不过将系数（很小的非零梯度）作为激活函数的参数，该参数和网络的其他参数一样，在训练过程中学习。

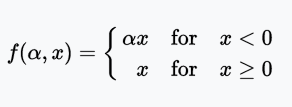
值域：(-∞, +∞)

RReLU函数

RReLU也类似Leaky ReLU，只不过系数（较小的非零梯度）在训练中取一定范围内的随机值，在测试时固定。

值域：(-∞, +∞)

ELU函数

ELU（Exponential Linear Unit，指数线性单元）尝试加快学习速度。基于ELU，有可能得到比ReLU更高的分类精确度。这里α是一个超参数（限制：α ≥ 0）。

值域：(-α, +∞)

SELU函数

SELU（Scaled Exponential Linear Unit，拉伸指数线性单元）是ELU经过拉伸的版本。

图片来源：Elior Cohen

SReLU函数

SReLU（S-shaped Rectified Linear Activation Unit，S型修正线性激活单元）由三个分段线性函数组成。系数作为参数，将在网络训练中学习。

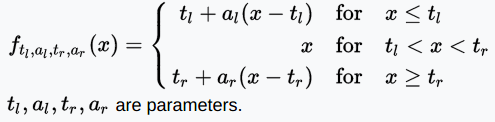
值域：(-∞, +∞)

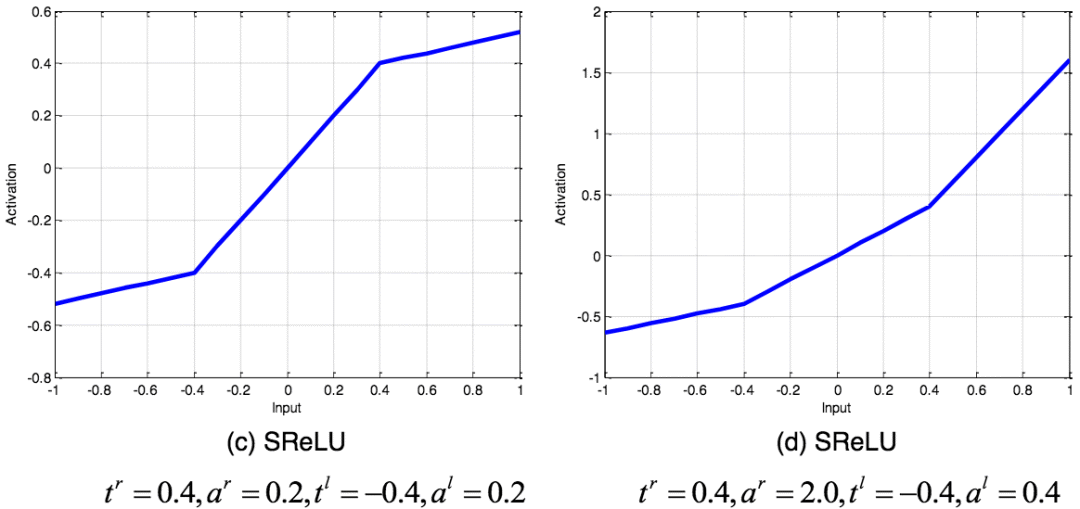
不同参数的SReLU图像；图片来源：arXiv:1512.07030

APL函数

APL（Adaptive Piecewise Linear，自适应分段线性）函数

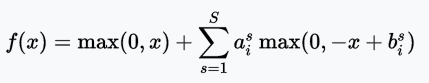
图片来源：arXiv:1512.07030

值域：(-∞, +∞)

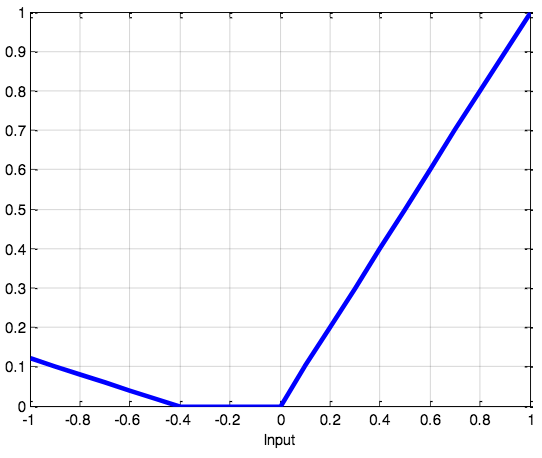
SoftPlus函数

SoftPlus函数的导数为逻辑（logistic）函数。大体上，ReLU和SoftPlus很相似，只不过SoftPlus在接近零处平滑可微。另外，计算ReLU及其导数要比SoftPlus容易很多。

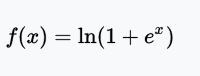
值域：(0, ∞)

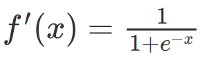
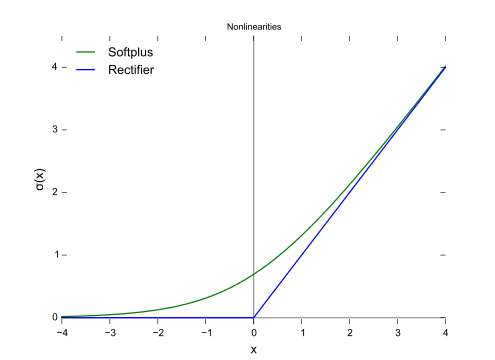
图片来源：维基百科

bent identity函数

bent identity函数，顾名思义，将恒等函数弯曲一下。

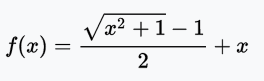
值域：(-∞, +∞)

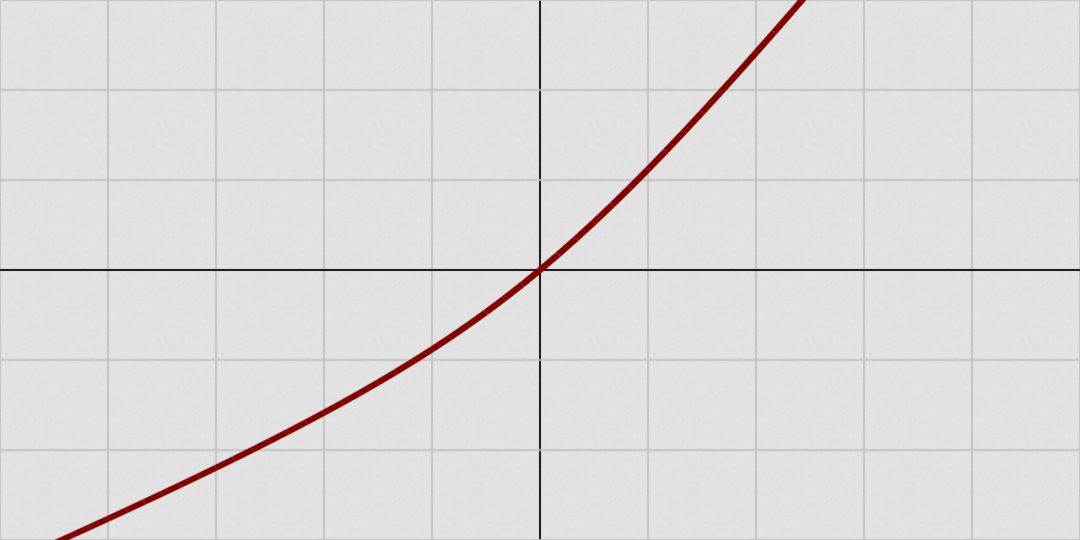
图片来源：维基百科

softmax函数

softmax函数将原始值转换为后验分布，可用于衡量确定性。类似sigmoid，softmax将每个单元的输出值挤压到0和1之间。不过，softmax同时确保输出的总和等于1.

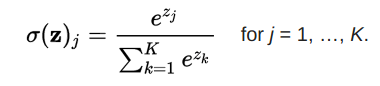
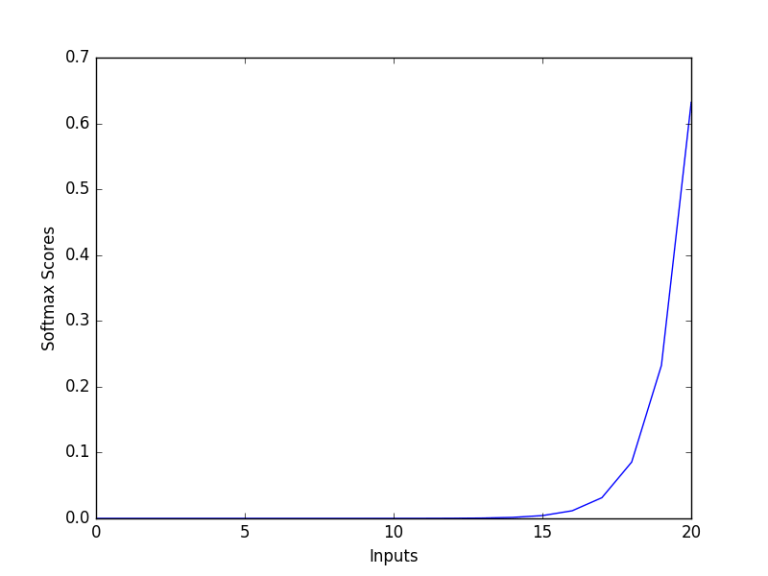
图片来源：dataaspirant.com

softmax函数的输出等价于类别概率分布，它告诉你任何分类为真的概率。

结语

选择激活函数时，优先选择ReLU及其变体，而不是sigmoid或tanh。同时ReLU及其变体训练起来更快。如果ReLU导致神经元死亡，使用Leaky ReLU或者ReLU的其他变体。sigmoid和tanh受到消失梯度问题的困扰，不应该在隐藏层中使用。隐藏层使用ReLU及其变体较好。使用容易求导和训练的激活函数。