在电子设计中,振荡器是一个重要的组件,广泛应用于信号发生、无线通信和音频设备中。一般来说,设计一个稳定的正弦波振荡器往往需要运算放大器或复杂的电路结构。
然而,是否可以仅用两个晶体管就轻松实现一个高效的正弦波振荡器呢?本文将介绍一种仅使用两个晶体管、少量无源元件以及简单反馈机制的正弦波振荡器设计,并分析其工作原理和性能。
电路结构与原理
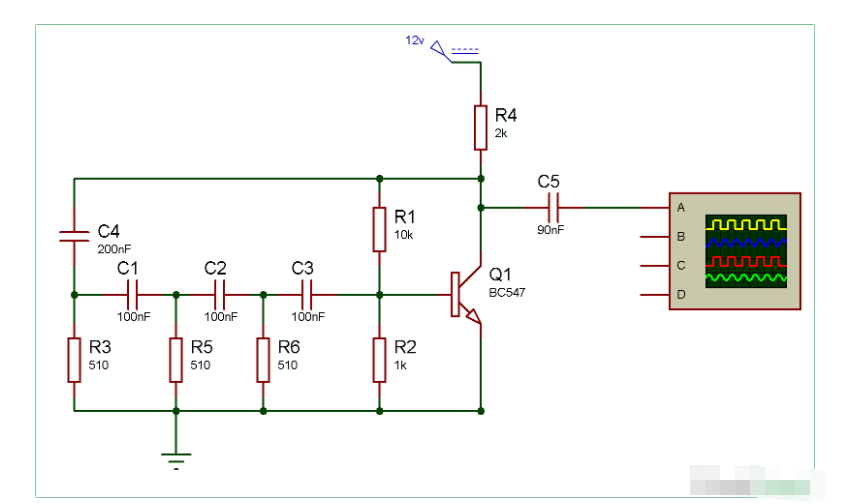
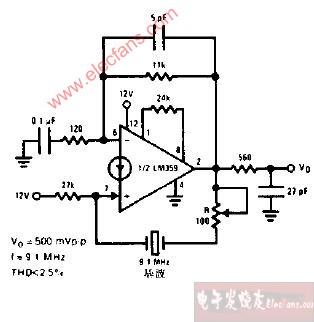
本文介绍的振荡器电路如图1所示。它由两个主要部分组成:一个基于晶体管Q1的多反馈带通滤波器(MFBF)和一个基于晶体管Q2的反相放大器。其中,多反馈带通滤波器负责设定振荡频率,而反相放大器提供增益以维持振荡。
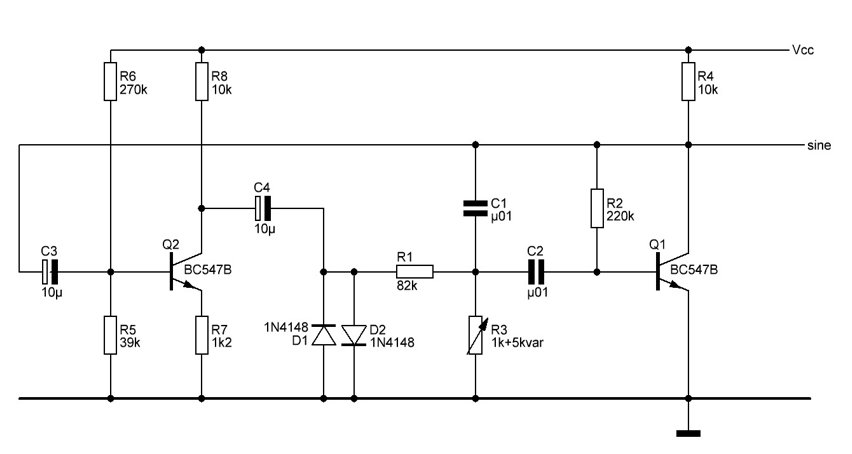 图1
图1多反馈带通滤波器(Q1部分)
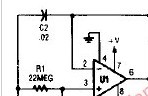
Q1及其周围的电路构成了多反馈带通滤波器。该滤波器的中心频率由无源元件(电阻和电容)决定,其典型结构如图2所示。
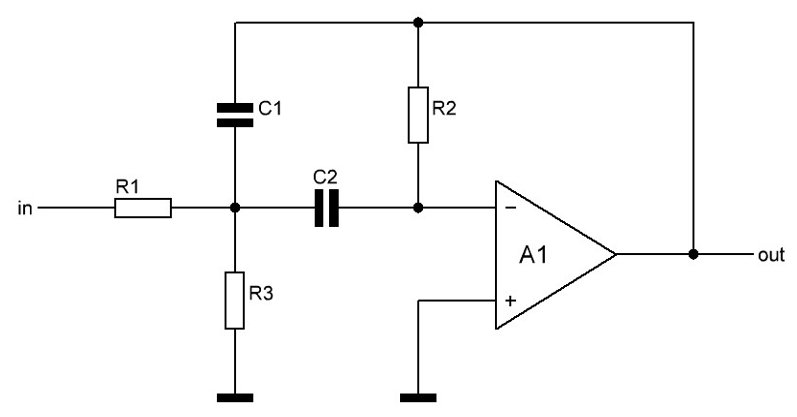 图2
图2滤波器的频率计算公式在大多数电子学教材中都可以找到(假设C1 = C2 = C):
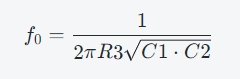
其中,R3的阻值决定了滤波器的中心频率,而R2和R1的比值决定了滤波器的增益,具体公式为:
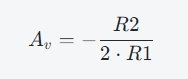
通常,这种滤波器使用运算放大器构建,但在本设计中,利用晶体管Q1实现了同样的功能。虽然晶体管开环增益有限,但在适当的频率范围内仍然可以满足振荡条件。
反相放大器(Q2部分)
由Q2构成的反相放大器为滤波器提供信号增益,同时确保回路总相移达到360°。Q2的增益由R8和R7的比值决定,具体公式为:
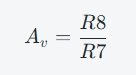
为了防止信号过载并保持正弦波的形状,R8与二极管D1、D2一起构成了一个限幅电路。当信号幅值超过一定阈值时,二极管导通,限制电压幅度,从而保证输出信号稳定。
振荡原理分析
在滤波器的中心频率处,滤波器的相移为180°,而Q2的反相特性又引入了额外的180°相移,使回路总相移为360°。同时,由于Q2提供了足够的增益,回路增益大于1,满足巴克豪森振荡条件,电路即可产生稳定的正弦波输出。
需要注意的是,滤波器的无源元件决定了中心频率。通过调整R3的阻值,可以改变振荡器的频率范围。本设计中,R3的调整范围为1kΩ到6kΩ,对应的输出频率范围为498 Hz至1230 Hz。
性能表现
实验表明,该振荡器电路具有良好的稳定性和较低的失真。输出信号的失真度约为1%,且输出幅值相对稳定。在电源电压从9V变化到12V时,振荡频率仅变化约2Hz,而输出幅值从0.80 Vpp变化到0.86 Vpp,表现出较强的抗干扰能力。
结语
通过巧妙设计,这款仅使用两个晶体管的振荡器电路实现了高效、稳定的正弦波输出,充分展现了电子设计中以简驭繁的艺术。这种电路设计不仅简洁实用,也为振荡器领域提供了新的思路,尤其适合对成本和元件数量有所限制的应用场景。
浮思特科技深耕功率器件领域,为客户提供IGBT、IPM模块等功率器件以及单片机(MCU)、触摸芯片,是一家拥有核心威廉希尔官方网站 的电子元器件供应商和解决方案商。
-
单片机
+关注
关注
6039文章
44575浏览量
636366 -
振荡器
+关注
关注
28文章
3839浏览量
139162 -
晶体管
+关注
关注
77文章
9705浏览量
138461
发布评论请先 登录
相关推荐
使用晶体管构建的简单正弦波发生器电路




 两个晶体管能如何实现高效正弦波振荡?
两个晶体管能如何实现高效正弦波振荡?

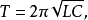










评论