一、加密算法概述
数据加密的基本过程就是对原来为明文的文件或数据按某种算法进行处理,使其成为不可读的一段代码为 “密文”,使其只能在输入相应的密钥之后才能显示出原容,通过这样的途径来达到保护数据不被非法人窃取、阅读的目的。该过程的逆过程为解密,即将该编码信息转化为其原来数据的过程。
1、常见加密算法
常见加密算法可分为三类,对称加密算法、非对称加密算法、Hash 加密算法
1.1 对称加密算法
特点是文件加密与解密使用相同的密钥,密钥较短。
优点:算法公开、加密速度快、计算量小、加密效率高。
缺点:加密方与解密方需要提前敲定好密钥,并双方保存好密钥。
常见对称加密算法:AES、SM4
1.2 非对称加密算法
可以在不传递密钥的情况下完成解密
优点:相比对称加密算法其安全性更好
缺点:加解密时间花费更长,适合少量数据加密
常见非对称加密算法:ECC、RSA、SM2
1.3 Hash 算法
算法特点是单向算法,不能通过 Hash 值还原目标信息
优点:不可逆、易计算、特征化
缺点:存在散列冲突(存在两个不同的原始值经过哈希运算后得到同样的结果)
常见非对称加密算法:SM3、SHA256、SHA384、SHA512、SHA224、SHA512_224、SHA512_25
二、ECC256 算法
ECC(Elliptic Curve Cryptography,椭圆曲线加密)算法公私钥的长度是 ECC 安全性的关键参数之一,ECC 算法后跟着的是椭圆曲线的域长度如 256 位,ECC256 是目前最常用的私钥长度之一,它提供了一个良好的安全性和性能的平衡。
1、ECC 算法原理介绍
1.1 概述
ECC(Elliptic Curve Cryptography)加密算法是一种基于椭圆曲线数学理论的公钥加密算法。
ECC 公钥:是基于私钥和椭圆曲线上的基点计算得出的,公钥在加密过程中用于接收者加密消息,在数字签名中用于验证签名。
ECC 私钥:是一个随机数,它在椭圆曲线加密算法中用于生成公钥以及在解密和签名过程中使用。
ECC 的安全性在很大程度上取决于曲线的选择,目前美国国家标准与威廉希尔官方网站 研究院(NIST)维护了一系列安全的椭圆曲线参数,即著名的 NIST 曲线。
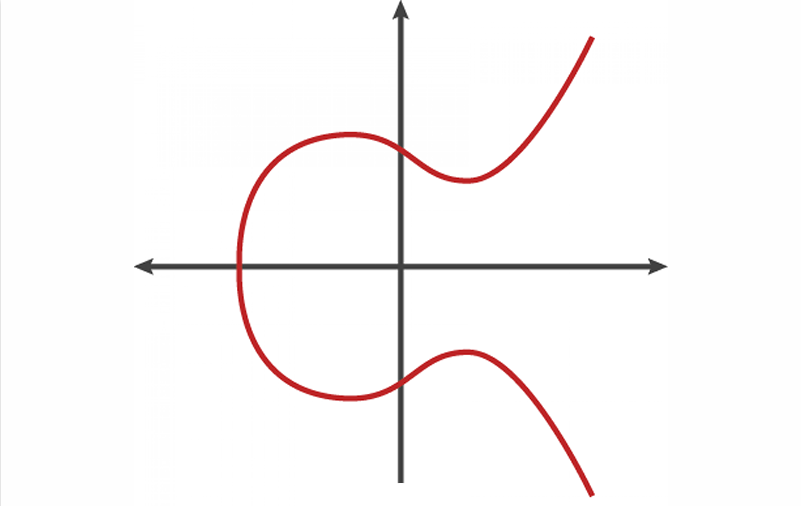
ECC 公钥长度的选择应根据安全要求和可用资源来确定,一般来说 256 位和 384 位的 ECC 公钥长度足以满足大多数应用的要求。
1.2 算法概念
椭圆曲线离散对数问题,椭圆曲线上的两个点 P 和 Q,P 称为基点(base point)、k 为私钥(private key)、Q 为公钥(public key)
Q = k * P
给定 k 和 P,根据加法法则,计算 Q 很容易;
但给定 P 和 Q ,求 k 非常困难(实际应用 ECC,质数 P 取的非常⼤,穷举出 k 非常困难)。
1.3 算法过程
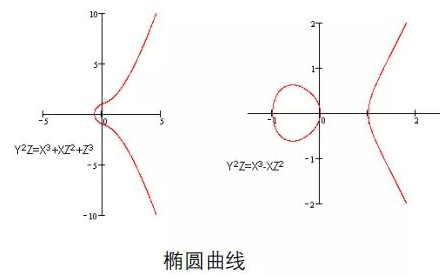
选⼀条椭圆曲线 Ep(a,b), 并取椭圆曲线上⼀点作为基点 P。
选定⼀个大数 k 作为私钥,并⽣成公钥 Q= k * P。
加密:选择随机数 r,将消息 M 生成密文 C,密文是⼀个点对,即 C = (rP, M+rQ)。
解密:M+rQ-k(rP) = M+r(kP)-k(rp) = M
1.4 算法过程解析
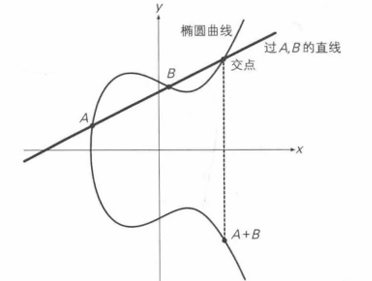
点运算的加法
过点 A B 交于曲线的一个交点,取这个交点 X 轴对称的点为 A+B
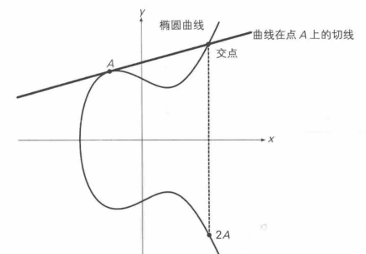
点运算的乘法
当 A 和 B 无限接近,A = B 时这条线为曲线上的切线,切线交于曲线的一个交点,取这个交点 X 轴对称的点为 A+A 即为 2A
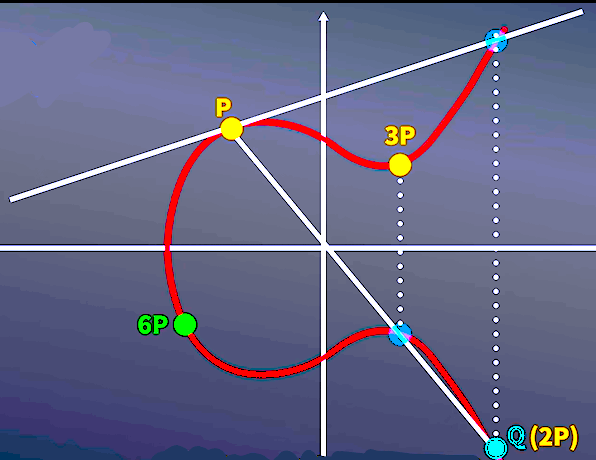
其中,6P 是由 3P 切线交线的来,也可由 2P 切线交线后 4P,再与 2P 交线的来
可得如下式子:
2(3P) = 3(2P)
密钥生成
私钥:选择一个大的随机整数 k 作为私钥。这个私钥应该保密,不应被泄露。
公钥:选择一个椭圆曲线上的基点 P(这个点是公开的,并且对于所有使用该曲线的用户都是相同的)。然后计算公钥 Q=kP,即私钥 k 与基点 P 的标量乘法结果,公钥 Q 可以公开。
加密过程
随机数:选择一个随机数 r,这个随机数在每次加密时都应该不同,以增加加密的安全性。
密文生成:将消息 M 编码为一个与椭圆曲线上的点可以相加的数值(这通常涉及到一些数学转换,比如将消息哈希为一个整数),然后计算密文 C,它是一个点对,即 C=(rP, M+rQ)。
rP 是随机数 r 与基点 P 的标量乘法结果。 M+rQ 是消息 M 与 rQ(即 r 与公钥 Q 的标量乘法结果)的加法,这里的加法是在椭圆曲线上的加法,不是普通的整数加法。
解密过程
解密过程:持有私钥 k 的用户可以解密密文 C。
从密文 C 中提取出 rP 和 M+rQ。
使用私钥 k 计算 k(rP)。
然后计算 M:(M+rQ)−k(rP)
由于 Q=kP,所以 rQ=r(kP)。因此:M = (M+rQ)−rQ=(M+rQ)−k(rP)=M+r(kP)−k(rP)
这样就成功地从密文中恢复出了原始消息 M。
安全性
ECC 的安全性基于椭圆曲线离散对数问题的难度,给定 P 和 Q=kP,很难计算出私钥 k。
加密过程中使用的随机数 r 增加了每次加密的多样性,使得即使相同的消息被多次加密,产生的密文也会不同。
2、ECC 算法公私钥数组长度
ECC 算法中,公钥和私钥的长度是固定的,并且与椭圆曲线的域长度(即 ECC256,256位)直接相关,以下是ECC256 算法中公钥和私钥的字节长度:
三、签名验签过程
因为 ECC 通常用于加密密钥交换或数字签名,而不是直接用于数据加密,所以签名验签过程分三部分:公钥生成、明文签名、签名验签。
1、公钥生成
1.1 密钥生成工具
OpenSSL 是一个强大的开源安全套接字层密码库,它提供了丰富的密码算法、密钥和证书封装管理功能,实现了目前大部分主流的密码算法和标准,如对称算法、非对称算法、散列算法、数字签名和认证、X509 数字证书标准、PKCS12、PKCS7 等。
特点:OpenSSL 是一个开源的软件库,用户可以自由地使用、修改和分发它
1.2 工具使用
在 Git 中集成了 OpenSSL 库,OpenSSL 主要作为一个加密库来使用,为 Git 的通信和数据存储提供安全支持,以下公钥生成章节中生成公钥等操作均在 Git 中调用 OpenSSL 库使用。
2、生成 ECC256 密钥
1.1 ECC256 公私私钥
① Eg. ECC256 算法生成公私钥 OpenSSL 命令
生成 ECC256 私钥
openssl ecparam -genkey -name prime256v1 -param_enc explicit -out secp256r1-key.pem
提取公钥
openssl ec -in secp256r1-key.pem -pubout -out ecpubkey.pem
打印私钥
openssl ec -in secp256r1-key.pem -text > pri.hex
打印公钥
openssl ec -pubin -in ecpubkey.pem -text > pub.hex
② 打开 pri.hex,查看文本,提取其中公钥与私钥数据
③ 提取出来的公钥与私钥数据数组如下:
// 软件工程中使用的公私钥
uint8 ecc_secp256r1_prikey[] = "ca085e45ec036d7a9bcd67d7990a89dd50816b9351141aafbbb75bb3c862cc51"
uint8 ecc_secp256r1_pubkey[] = "f227f1bd2dd624e211580207e248fcc077bc5a5a5877128d85e25a3aedb24b98b0efd869cd9953ca5aed03b9b4528164d2cbf203b35f391d3cd573aebd78646e"
3、ECC256 签名
签名方需要待签名数据 test_data_raw.bin,需要 ECC256 密钥 secp256r1-key.pem
① 生成签名数据的哈希,首先对待加密数据文件的内容生成一个哈希值,使用 SHA-256 算法来完成。
# 生成文件的 SHA-256 哈希值
openssl dgst -sha256 -binary -out hash.bin test_data_raw.bin
② 使用 ECC 私钥签名上一步骤生成的哈希值。
# 使用 ECC 私钥对哈希值进行签名
openssl dgst -sha256 -sign secp256r1-key.pem -out signature.bin hash.bin
将签名转换为十六进制表示(用于查看)
openssl base64 -in signature.bin -out signature.hex
③ 对 test_data_raw 的哈希值进行签名,签名数据转为 hex 查看
4、ECC256 签名验签
验签方需要待签名数据 test_data_raw.bin、由 ECC256 密钥 secp256r1-key.pem 中提取的 ecpubkey.pe公钥。
① 重新生成签名数据的哈希,接收方在收到数据和签名后,首先需要对数据重新生成哈希值,使用 SHA-256 算法来完成。
# 接收方重新生成文件的 SHA-256 哈希值
openssl dgst -sha256 -binary -out received_hash.bin test_data_raw.bin
② 使用公钥验签:然后,接收方使用 ECC256 公钥对签名进行验证,以确保数据在传输过程中没有被篡改。
# 使用公钥验证签名
openssl dgst -sha256 -verify ecpubkey.pem -signature signature.bin data_hash.bin
③ 如果签名验证成功,OpenSSL 不会输出任何内容(或者可能会输出一个 "Verified OK" 的消息,这取决于你的 OpenSSL 版本和配置);
如果验证失败,OpenSSL 会输出一个错误消息,指出签名无效;
printf >>
$ openssl dgst -sha256 -verify ecpukey.pem -signature signature.bin hash.bin
Verified OK
四、参考文档
《【ECC加密算法】| ECC加密原理详解| 椭圆曲线加密| 密码学| 信息安全》
https://www.bilibili.com/video/BV1v44y1b7Fd/?spm_id_from=333.337.search-card.all.click&vd_source=9fe0b02e4f116cc091f5fa76d03c35c6
《Openssl》
https://www.openssl.org/
《椭圆加密算法》
https://baike.baidu.com/item/%E6%A4%AD%E5%9C%86%E5%8A%A0%E5%AF%86%E7%AE%97%E6%B3%95/10305582?fr=ge_ala
登录大大通网站,阅读原文,提问/评论,获取威廉希尔官方网站 文档等更多资讯!
-
密钥
+关注
关注
1文章
139浏览量
19775 -
加密算法
+关注
关注
0文章
216浏览量
25551 -
数据加密
+关注
关注
0文章
53浏览量
12723
发布评论请先 登录
相关推荐
基于椭圆曲线算法的数字签名威廉希尔官方网站 研究
三种加密器件的熟悉
基于STM32的C语言SHA256加密算法相关资料下载
基于AES和ECC的混合加密系统的设计
基于ECC加密的电子商务系统
基于AES加密算法的信息安全研究(AEC与ECC结合)
常见公钥加密算法有哪些
基于STM32的C语言SHA256加密算法





 深入解析ECC256椭圆曲线加密算法
深入解析ECC256椭圆曲线加密算法
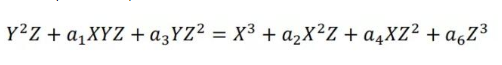










评论