由于定点的四则运算比较简单,如加减法只要注意符号扩展,小数点对齐等问题即可。在本文中,运用在前一节中描述的自定义浮点格式FPGA中数的表示方法(下),完成浮点四则运算的实现过程
1.自定义浮点格式加(减)法运算
基于FPGA 实现的浮点加法运算包括了一系列对尾数和指数部分的操作:移位、交换、格式化、舍入和格式化等。如下图所示,自定义浮点流水加法器实现结构主要分为两部分:基本加法器部分和格式化操作部分。
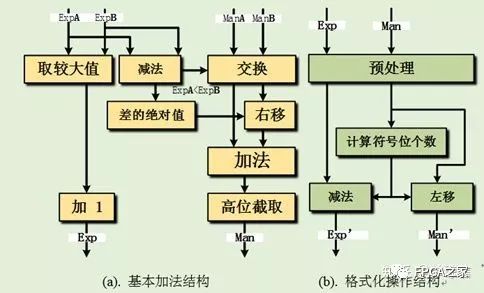
在图(a)中的基本加法器,首先比较两个操作数的指数部分,较大的指数加上1之后,寄存输出(保证流水输出)作为加法和的指数部分;另一方面根据指数部分的比较结果,交换尾数的位置,即需要对较小的尾数进行右移对齐;之后尾数部分相加,得到的结果高位截取后输出作为加法和的尾数部分。由于操作数A 和B 的尾数部分首先需要符号位拓展之后进行才进行下一步操作,而最后的和是直接高位截取输出的,故导致加法结果比实际值小一倍,这就是前面指数需要加上1输出的原因。对于(b)中的格式化操作,首先对来自基本加法器的尾数和指数进行预处理,然后计算尾数部分的符号位个数。最后根据计算得到的符号位个数,左移尾数后输出尾数部分,而指数则减去符号位数作为指数部分输出。
如果是一次而输入加法则以这样的结构即可,但如果涉及多次加法,以流水形式完成,则在结构上可以作更好的优化。如下是四输入和八输入加法器的结构:
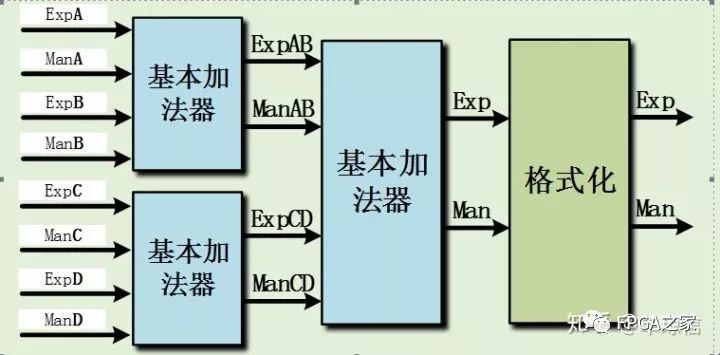
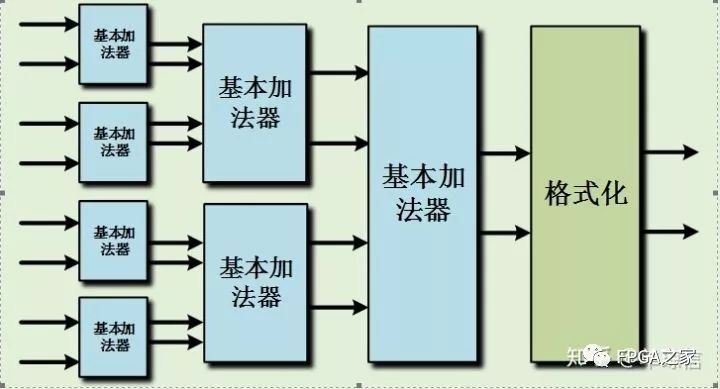
如上所示的情况,可知,这样的方法可以减少格式化操作,而格式化操作在整个运算过程中消耗相对比较多的资源,因此这样的实现结构可以有效的减少硬件资源的消耗。
3. 乘加运算
浮点乘法运算较为简单,对应的尾数部分进行相乘,指数部分进行相加。尾数相乘部分采用XILINX 乘法器IP即可。需要注意的是,乘法结果输出的位宽指定,在乘法器IP中,按一般流程下来,乘完之后的结果是保留两位符号位(假设乘数都是一个符号的情况),即多出一个符号位,按小数乘法分析的话,值的情况是比实际结果小一倍,在截位输出的时候需要做一定的取舍(是从最高位开始截位输出,还是次高位开始截位输出;如果从最高位截位输出,则结果比实际值小一倍,如果从次高位截位输出只有一种情况会溢出,即两个乘数都为-1的情况,这种情况如果从次高位截位输出则会错误,其余情况都是正确的)。
这里需要进一步讨论的是乘加操作,数字信号处理中常常会遇到操作,如FIR滤波器。按本文的设计思路乘加运算也可以节省一次格式化运算,设计方法如下:
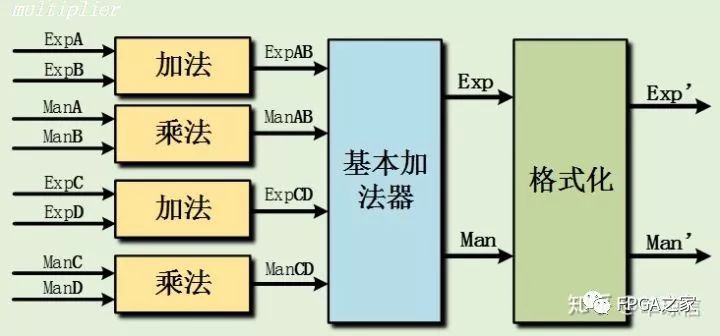
这样即可省去乘法器中的格式化过程,将乘法的中间结果直接输入给加法器,最后再进行格式化输出。
4. 自定义浮点除法器详细设计
现有的除法硬件实现算法主要可以分为三类:查表法、数字迭代法和函数迭代法。基于查找表的实现方法实现结构简单,只需进行简单的查表操作即可,但是其精度多一位,则查找表大小就要增加一倍,显然不适合实现高精度除法器;数字迭代法中应用最广的是SRT算法,这类算法基于减法运算,商的精度随减法迭代次数而线性增长,故为了得到高精度,资源消耗也是相当严重。函数迭代算法中最典型的两种算法是Newton Raphson和Goldschimidt算法,这两种算法是采用乘法运算来实现对商的精度的逼近,商的精度随着迭代次数而呈指数增长,适用于高精度的除法运算。
本质上Goldschimidt和Newton Raphson两种算法的原理是一致的,Goldschimidt算法的实质就是对牛顿迭代算法的迭代操作进行重新排列,使得Goldschimidt算法中的乘法操作可以并行进行处理,故在利用硬件实现除法时,Goldschimidt算法较Newton Raphson在速度上更具优势。以下详细分析一下Goldschmidt算法的原理
函数g(y)在p点的泰勒展开公式如下:
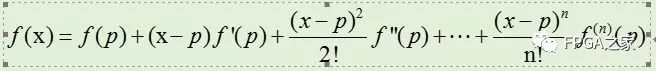
对于除法来说,希望得到如下的等式关系:
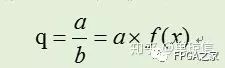
即可以得到倒数函数的展开公式,然而,倒数函数无法作泰勒展开,故采用麦克劳林展开公式,采用的函数表达如下:
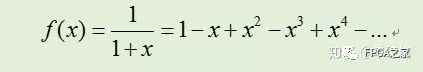
令 f(x)=1/b,则有x=b-1,由0.5≤b<1,得abs(x)≤0.5 ,故:
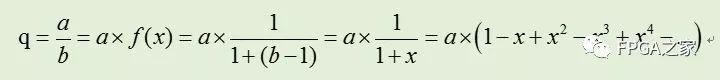
上述公式因式分解后可得如下公式:
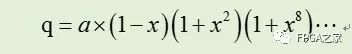
q值可以实现如下迭代过程,其近似的商可以表示如下:
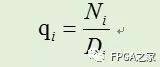
其中Ni和Di分别是算法执行i步后得到的分子和分母。当Di趋近1时,Ni就趋近于q了。迭代开始时,令N0=a,D0=b。第一次迭代,时,N1=R0*N0,其中R0= 1-x = 2-b。可得到如下:
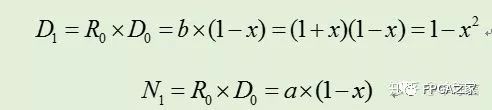
类似地,下次迭代令R1= 2-D1= 1+y^2,则可以得到:
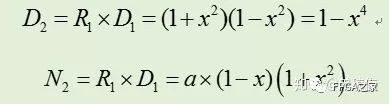
故可以得到Goldschmidt算法的迭代过程,总结如下:
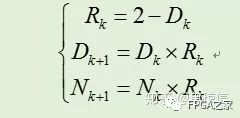
故通过对初始种子进行多次迭代而不断逼近目标精度。
现有的Glodschimidt算法都是基于标准的IEEE 754双精度格式,其算法过程可以描述如下图所示:
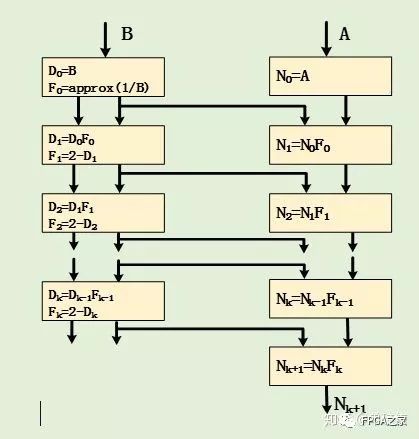
上图中的approx(1/B)步骤需要得到精度不高的近似的倒数,这里采用直接查找表的形式,这种形式最为简单,直接查找倒数表得到除数(B)的倒数近似值,然后在使用该值进行上图所示的函数迭代来得到更高精度的除数倒数逼近值。直接查找表得到的近似值的精度取决于查表的索引长度及其表项长度。故要使初始值的精度增加1位,则查找表的空间就需要翻一倍。对于现阶段的FPGA,其存储资源已经非常多,故在FPGA实现直接查找表,其资源消耗是相对很小的。
IEEE-754标准的浮点数尾数的值范围为[1,2),在不考虑符号位的情况下,尾数D形如1.d1d2d3…dn。则其倒数范围(0.5,1]。而自定义的浮点的尾数格式为 .1d1d2d3…dn, 即表示的值的范围[0.5,1),则其倒数范围为(1,2]。这样的区别导致在整个大框架下具体的实现内容情况发生变化。需要对整个算法的每一步骤做好设计。
诚如上述,自定义格式的浮点中,得到的倒数范围为(1,2],而我们自定义的浮点格式表示的范围为[0.5,1),故我们须将(1,2]改成(0.5,1] * 2,其中的(0.5,1]由尾数表示,而2则由指数表示。故查找表中的表项表示的值是实际倒数值的1/2。现假设阶段后的除数输入表示为0.1d1d2d3…dn,则输出的除数倒数值可表示为21 * 0.1b1b2b3…bm,则查表所需的查找表大小为:
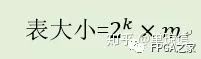
而在FPGA中,采用块RAM进行实现,每个块RAM大小36k,而本实现中,初始精度的设计需要达到14位左右,这样,则输出位宽m表示为13至16都消耗同等资源,而后边的算法迭代中,设计的乘法器位宽当为有符号数16x52消耗的DSP48乘法模块的资源为3,是最为折中的方法,故采用m为15,直接查找表中的每一项直接表示为0.1b1b2b3…bm,这样表的输出为16位,正好与后边的乘法器位宽对应上。
4.1 查找表设计
直接查找表方法中,最常用的是常数分段逼近方法,该算法的核心是确定截断输入数0.1d1d2d3…dn0和后一位截断输入数0.1d1d2d3…dn1,的中点数值,然后计算该值的倒数,最后加上2^(-(m+2)),并对得到的结果进行舍入到0.1b1b2b3…bm,故查找表中的每一项可以表示为:
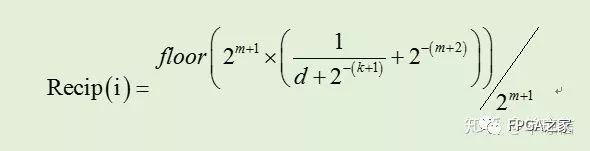
其中0.1d1d2d3…dn。对于输出位宽m=k+g,能得到的设计精度如下表格:
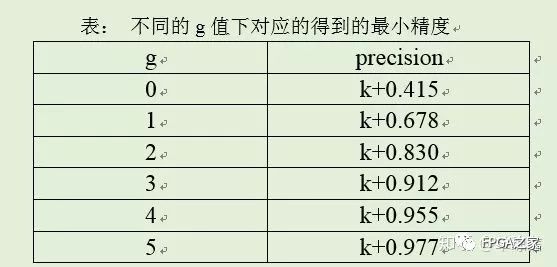
假设确定k=13,m=16,故得到的最小精度为13.912。
4.2 迭代过程
对应的函数迭代过程也发生相应地改变,这里设计时应该考虑每一步骤中的指数变化情况。相应的设计过程如下图所示:
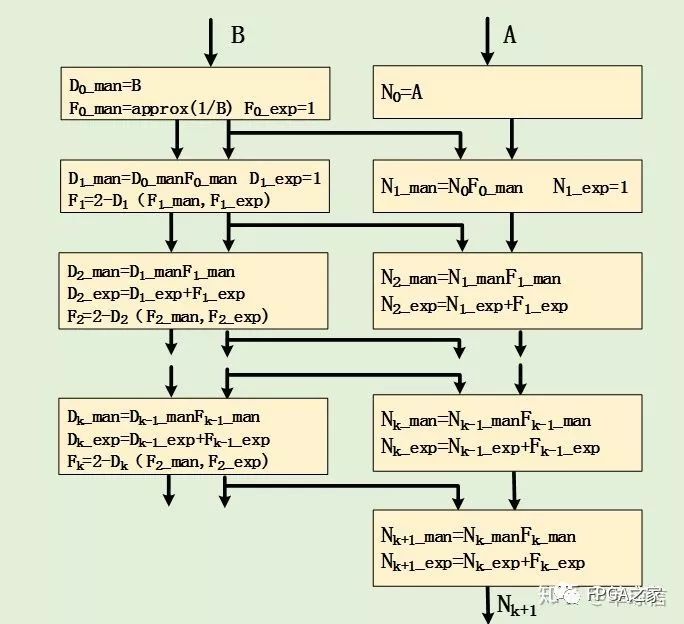
另外在实现多分子单分母,形如(A+C)/B,为了更省时间和空间资源可以采取如下图所示的实现策略:
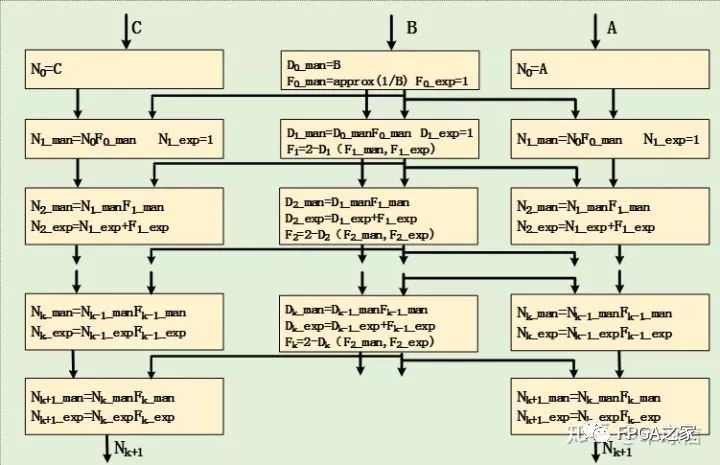
整个算法的流水过程如下:
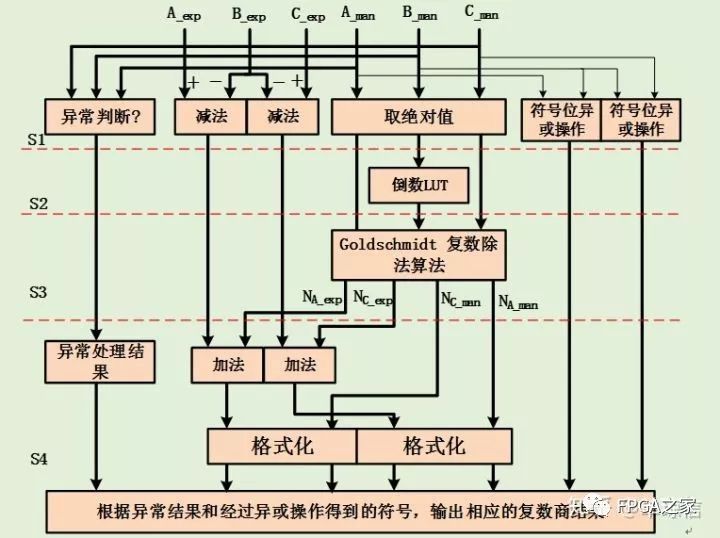
至此,完成自定义浮点格式的四则运算。
-
FPGA
+关注
关注
1629文章
21729浏览量
603024 -
运算
+关注
关注
0文章
130浏览量
25785
原文标题:FPGA中的浮点四则运算
文章出处:【微信号:Hack电子,微信公众号:Hack电子】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
雾盈FPGA笔记之(二十五)六位数四则运算计算器(1)整体结构及设计思路
雾盈FPGA笔记之(三十)六位四则运算计算器(6)小算法实现BCD转二进制
雾盈FPGA笔记之(三十二)六位四则运算计算器(8)算法实现加减乘除
利用simulink设计四则运算仿真模型
如何去实现基于单片机的四则运算计算器设计
使用51单片机设计一个四则运算带括号的计算器设计报告免费下载
使用51单片机实现简易四则运算计算器的资料和程序免费下载
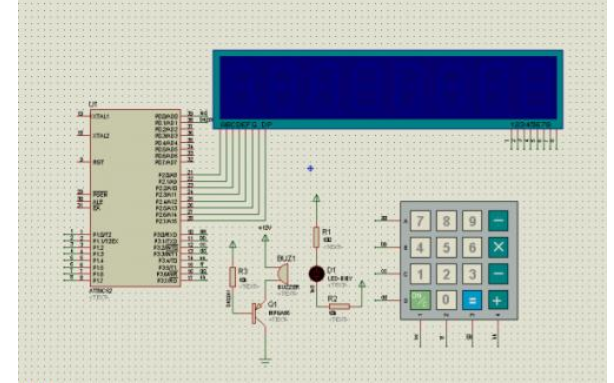
三菱FX系列PLC浮点数运算指令说明
基于单片机四则运算计算器设计+proteus仿真





 FPGA中浮点四则运算的实现过程
FPGA中浮点四则运算的实现过程










评论