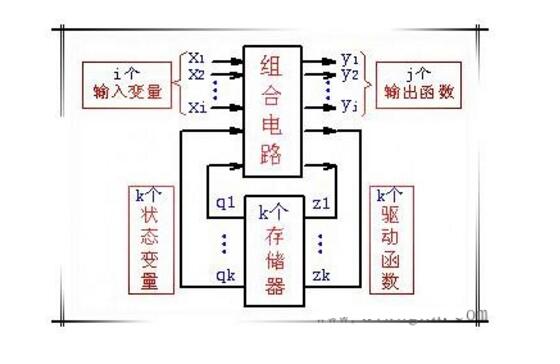
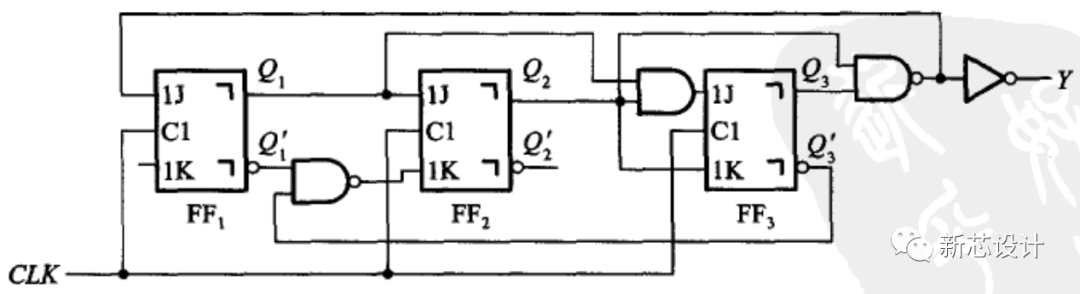
时序逻辑电路是数字电路中的一种重要类型,它具有存储功能,能够根据输入信号和内部状态的变化来改变其输出。时序逻辑电路广泛应用于计算机、通信、控制等领域。本文将介绍时序逻辑电路的描述方法,包括状态图、状态表、有限状态机、卡诺图、布尔差分方程、布尔函数、时序逻辑仿真等。
- 状态图
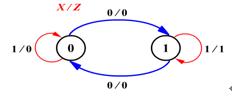
状态图是一种图形化的描述方法,用于表示时序逻辑电路的状态转换关系。状态图由节点和有向边组成,节点表示电路的状态,有向边表示状态之间的转换。状态图的绘制步骤如下:
1.1 确定状态集合:首先需要确定电路的所有可能状态,并将它们表示为状态集合。
1.2 确定初始状态:在状态集中选择一个状态作为初始状态。
1.3 确定输入变量:确定电路的输入变量,它们将影响状态转换。
1.4 绘制状态转换:根据电路的逻辑功能,绘制状态之间的转换关系。对于每个状态,列出所有可能的输入变量组合,并确定它们对应的下一个状态。
1.5 标注状态转换条件:在有向边旁边标注状态转换的条件,通常使用布尔表达式表示。
1.6 检查状态图的完整性:确保状态图包含了所有可能的状态转换。
- 状态表
状态表是一种表格化的描述方法,用于表示时序逻辑电路的状态转换关系。状态表通常包括以下几列:当前状态、输入变量、输出变量和下一个状态。状态表的编制步骤如下:
2.1 确定状态集合:与状态图相同,首先确定电路的所有可能状态。
2.2 列出输入变量:确定电路的输入变量,并在状态表的左侧列出它们。
2.3 列出输出变量:确定电路的输出变量,并在状态表的右侧列出它们。
2.4 填充状态表:对于每个状态和输入变量的组合,确定下一个状态和输出变量,并将它们填入状态表中。
2.5 检查状态表的完整性:确保状态表包含了所有可能的状态转换。
- 有限状态机(FSM)
有限状态机是一种抽象的计算模型,用于描述时序逻辑电路的状态转换关系。有限状态机由一组状态、一组输入变量、一组输出变量和一组状态转换规则组成。有限状态机的描述方法包括:
3.1 确定状态集合:与状态图和状态表相同,首先确定电路的所有可能状态。
3.2 确定初始状态:在状态集中选择一个状态作为初始状态。
3.3 确定输入变量:确定电路的输入变量,它们将影响状态转换。
3.4 确定输出变量:确定电路的输出变量,它们将根据状态转换结果产生。
3.5 确定状态转换规则:根据电路的逻辑功能,确定状态转换规则。状态转换规则通常使用布尔表达式表示。
3.6 描述有限状态机:使用状态图或状态表描述有限状态机的状态转换关系。
- 卡诺图
卡诺图是一种图形化的优化方法,用于简化布尔函数。卡诺图的绘制步骤如下:
4.1 列出布尔函数的真值表:首先列出布尔函数的所有可能输入组合及其对应的输出值。
4.2 绘制卡诺图:根据输入变量的数量,绘制相应大小的卡诺图。卡诺图由单元格组成,每个单元格对应一个输入组合。
4.3 标记1值:在卡诺图中,将真值表中的1值对应的单元格标记出来。
4.4 寻找覆盖1值的最小集合:在卡诺图中,寻找能够覆盖所有1值的最小单元格集合。这些单元格集合可以共享边或顶点。
4.5 简化布尔函数:使用找到的最小单元格集合,构造简化后的布尔函数。
- 布尔差分方程
布尔差分方程是一种代数化的描述方法,用于表示时序逻辑电路的状态转换关系。布尔差分方程的建立步骤如下:
5.1 确定状态变量:首先确定电路的状态变量,它们将表示电路的状态。
5.2 确定输入变量:确定电路的输入变量,它们将影响状态转换。
5.3 建立状态方程:根据电路的逻辑功能,建立状态变量与输入变量之间的关系,通常使用布尔表达式表示。
5.4 建立输出方程:根据状态变量和输入变量,建立输出变量与它们之间的关系,通常使用布尔表达式表示。
5.5 求解布尔差分方程:使用布尔代数的运算规则,求解布尔差分方程,得到电路的状态转换关系。
-
数字电路
+关注
关注
193文章
1605浏览量
80617 -
时序逻辑电路
+关注
关注
2文章
94浏览量
16541 -
函数
+关注
关注
3文章
4331浏览量
62593 -
输入信号
+关注
关注
0文章
456浏览量
12562
发布评论请先 登录
相关推荐
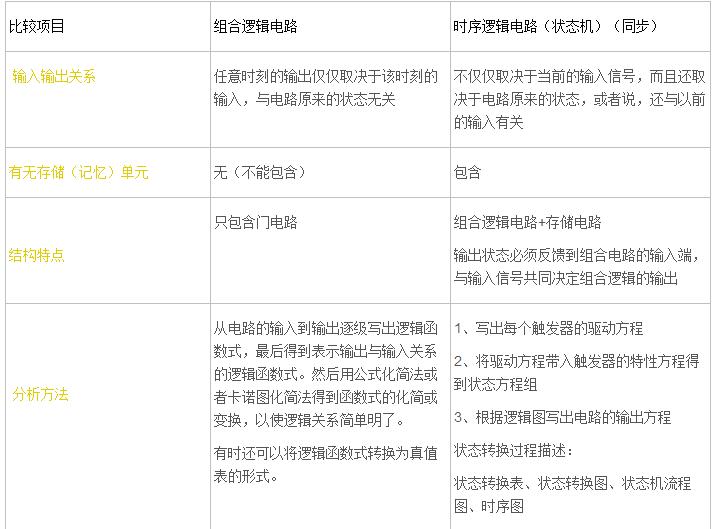
组合逻辑电路和时序逻辑电路比较_组合逻辑电路和时序逻辑电路有什么区别
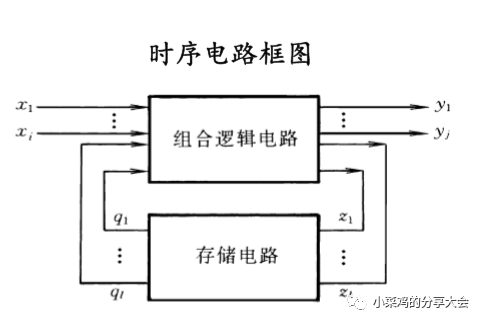
时序逻辑电路的分析方法




 时序逻辑电路的描述方法有哪些
时序逻辑电路的描述方法有哪些











评论