单片机高效运行秘诀：实现数学函数的优化之道

大家好，我是小麦，今天给大家分享一下如何在资源紧张，算力较低的单片机上实现三角函数的算法。

之前发过一篇关于IQMath的文章，这个是ti公司平台上的一个数学运算库，里面封装了很多高效的数学运算方法。

例如在不具备浮点运算器的定点处理器使用定点运算，以前写过一篇Q格式的文章，有简单介绍过这些知识。

那么问题来了，有一个读者朋友的硬件平台无法使用IQMath，但是他要进行一些三角函数的运算，那么该如何自己动手实现呢？

下面我们来简单介绍一下整体的思路吧，因为硬件平台的资源比较紧张；

RAM比较少；

ROM比较少；

CPU处理速度比较慢；

所以这里比较常用的方法就是通过空间换时间，预先将sin，cos的值存储到数组中，需要用的时候，访问数组就可以得到具体的数据。这也就是我们经常会提到的查表法。

下面我们来详细介绍一下。

正弦表

这个正弦函数表达式是这样的，

具体如下图所示；

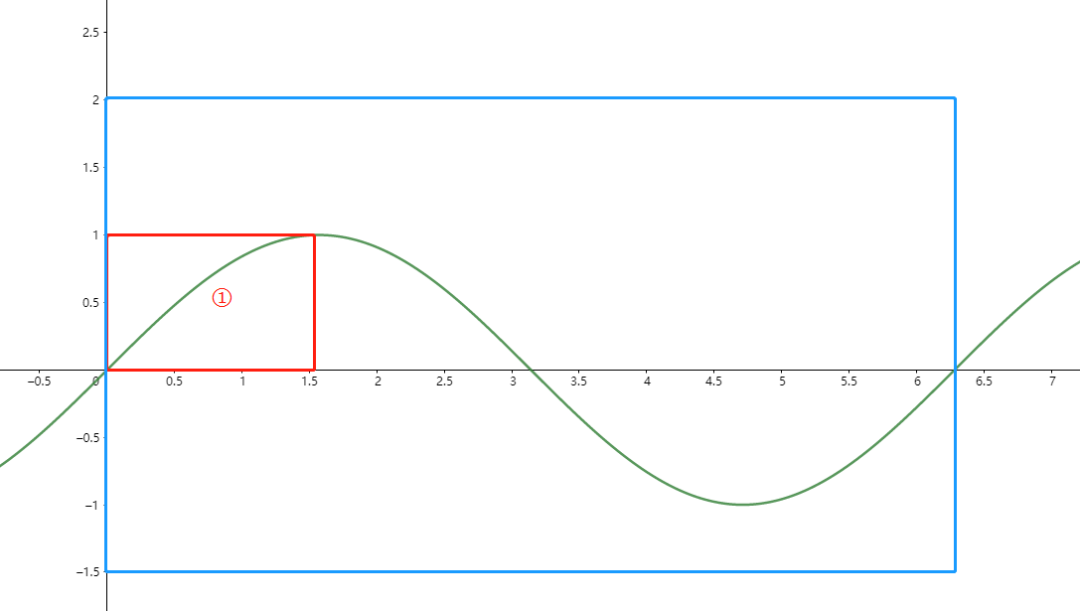
正弦波

首先我们来简单分析一下这个波形：

在蓝色框内是一整个周期的波形；

在红色框内是四分之一个周期的波形；

其实不难发现，我们只要表示出这四分之一个波形的数据，其余剩下的波形都可以通过换算表示出来。

这样做就大大节省了查表法所需要的空间。

下面我们来介绍一下具体如何实现；

首先我们得搞清楚一个点，就是量纲，统一用归一化的形式来做。

y的范围是 [-1, 1]；

x的范围是[0, 2π]，当然，x的范围[-π, π]也是没问题的，下面会继续介绍；

而在实际的程序中，我们是无法这样去做的，这些数值我们期望通过整形类型去访问，所以我们要做到几点：

尽量避免使用浮点运算；

尽量避免除法；

尽量避免乘法；

所以这里有必要先了解一下Q格式，用左移和右移去代替乘法和除法，提高运算效率；

对于X轴的数据，于是可以将[0, 2π]细分成 128 ，256，512或者 1024 等等；

这里我们先细分成1024等份，正如前面提到的，只需要选择前四分之一周期的内容即可；

#definePOINT_NUM256
#definePI3.141592f
for(inti=0;i< POINT_NUM; i++) {

        printf( "[%03d:%1.4f]	", i , (sin(i*PI/2 / POINT_NUM)));
        if((i+1) % 8 == 0){
            printf("
");
        }
    }

打印的输出结果如下：

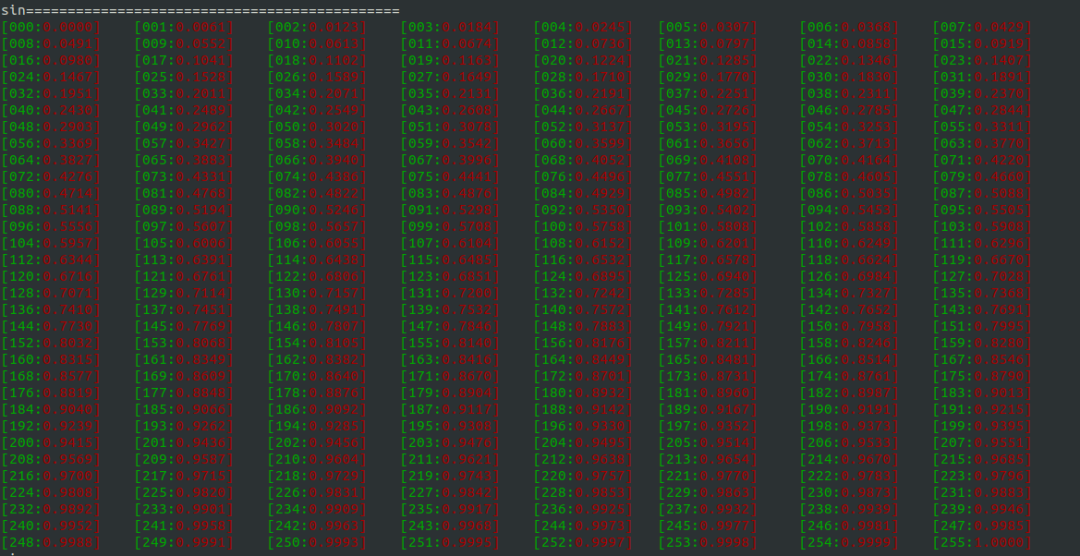
浮点类型的正弦表

这里我们可以简单取几个特殊点验证一下，发现整体还是可以接受的；

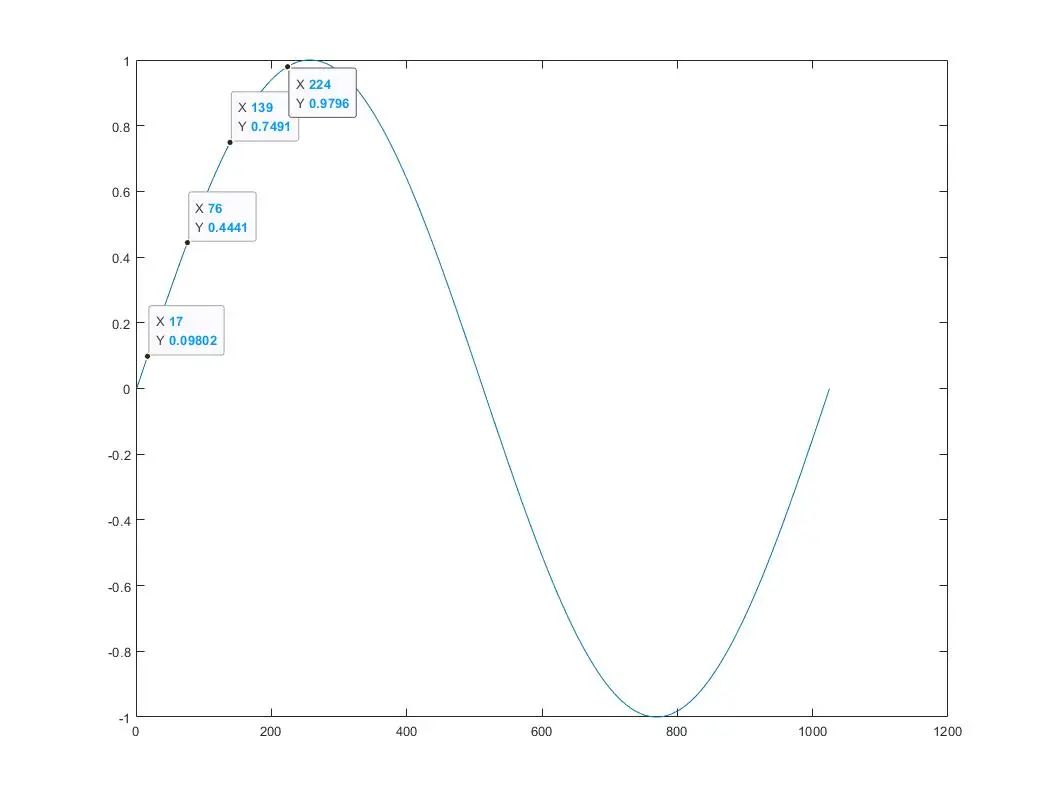
matlab输出的波形

下一步就是将浮点数据y转化为Q1.15格式哈，

#definePOINT_NUM256
#definePI3.141592f
printf("sin=============================================
");
for(inti=0;i< POINT_NUM; i++) {

        printf("[ %d:	0x%04X ]", i, (int16_t)(sin(i*PI/2 / POINT_NUM) * 32768));
        if((i+1) % 8 == 0){
            printf("
");
        }
    }

最终输出结果如下所示；

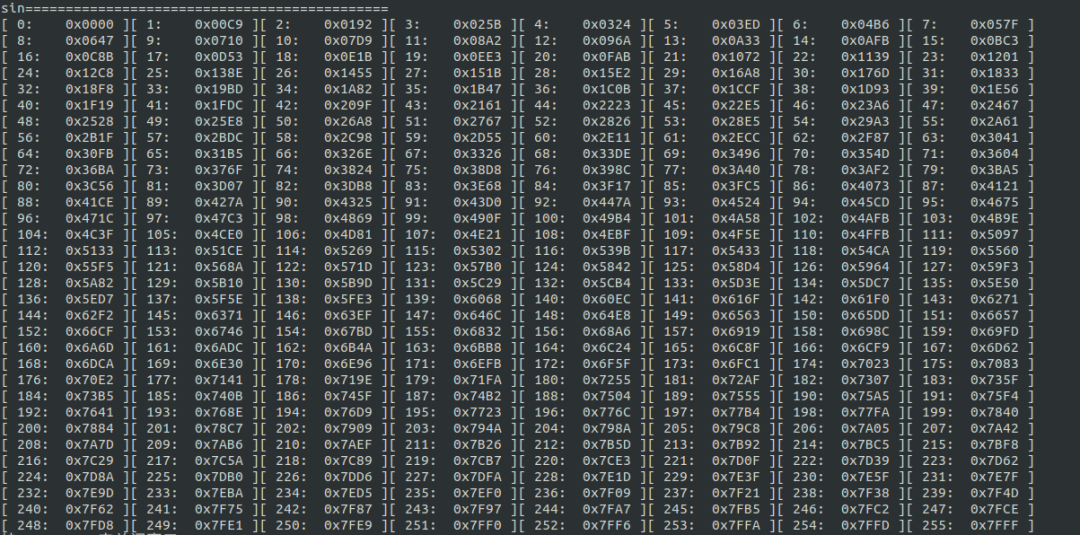
Q格式正弦表

源码部分

下面这部分代码是参考ST的mcsdk中的一个实例，下面我们会依次分析每个部分的作用，整体的代码具体如下所示；

#defineSIN_COS_TABLE{
0x0000,0x00C9,0x0192,0x025B,0x0324,0x03ED,0x04B6,0x057F,
0x0648,0x0711,0x07D9,0x08A2,0x096A,0x0A33,0x0AFB,0x0BC4,
0x0C8C,0x0D54,0x0E1C,0x0EE3,0x0FAB,0x1072,0x113A,0x1201,
0x12C8,0x138F,0x1455,0x151C,0x15E2,0x16A8,0x176E,0x1833,
0x18F9,0x19BE,0x1A82,0x1B47,0x1C0B,0x1CCF,0x1D93,0x1E57,
0x1F1A,0x1FDD,0x209F,0x2161,0x2223,0x22E5,0x23A6,0x2467,
0x2528,0x25E8,0x26A8,0x2767,0x2826,0x28E5,0x29A3,0x2A61,
0x2B1F,0x2BDC,0x2C99,0x2D55,0x2E11,0x2ECC,0x2F87,0x3041,
0x30FB,0x31B5,0x326E,0x3326,0x33DF,0x3496,0x354D,0x3604,
0x36BA,0x376F,0x3824,0x38D9,0x398C,0x3A40,0x3AF2,0x3BA5,
0x3C56,0x3D07,0x3DB8,0x3E68,0x3F17,0x3FC5,0x4073,0x4121,
0x41CE,0x427A,0x4325,0x43D0,0x447A,0x4524,0x45CD,0x4675,
0x471C,0x47C3,0x4869,0x490F,0x49B4,0x4A58,0x4AFB,0x4B9D,
0x4C3F,0x4CE0,0x4D81,0x4E20,0x4EBF,0x4F5D,0x4FFB,0x5097,
0x5133,0x51CE,0x5268,0x5302,0x539B,0x5432,0x54C9,0x5560,
0x55F5,0x568A,0x571D,0x57B0,0x5842,0x58D3,0x5964,0x59F3,
0x5A82,0x5B0F,0x5B9C,0x5C28,0x5CB3,0x5D3E,0x5DC7,0x5E4F,
0x5ED7,0x5F5D,0x5FE3,0x6068,0x60EB,0x616E,0x61F0,0x6271,
0x62F1,0x6370,0x63EE,0x646C,0x64E8,0x6563,0x65DD,0x6656,
0x66CF,0x6746,0x67BC,0x6832,0x68A6,0x6919,0x698B,0x69FD,
0x6A6D,0x6ADC,0x6B4A,0x6BB7,0x6C23,0x6C8E,0x6CF8,0x6D61,
0x6DC9,0x6E30,0x6E96,0x6EFB,0x6F5E,0x6FC1,0x7022,0x7083,
0x70E2,0x7140,0x719D,0x71F9,0x7254,0x72AE,0x7307,0x735E,
0x73B5,0x740A,0x745F,0x74B2,0x7504,0x7555,0x75A5,0x75F3,
0x7641,0x768D,0x76D8,0x7722,0x776B,0x77B3,0x77FA,0x783F,
0x7884,0x78C7,0x7909,0x794A,0x7989,0x79C8,0x7A05,0x7A41,
0x7A7C,0x7AB6,0x7AEE,0x7B26,0x7B5C,0x7B91,0x7BC5,0x7BF8,
0x7C29,0x7C59,0x7C88,0x7CB6,0x7CE3,0x7D0E,0x7D39,0x7D62,
0x7D89,0x7DB0,0x7DD5,0x7DFA,0x7E1D,0x7E3E,0x7E5F,0x7E7E,
0x7E9C,0x7EB9,0x7ED5,0x7EEF,0x7F09,0x7F21,0x7F37,0x7F4D,
0x7F61,0x7F74,0x7F86,0x7F97,0x7FA6,0x7FB4,0x7FC1,0x7FCD,
0x7FD8,0x7FE1,0x7FE9,0x7FF0,0x7FF5,0x7FF9,0x7FFD,0x7FFE}

constint16_thSin_Cos_Table[256]=SIN_COS_TABLE;

typedefstruct
{
int16_thCos;
int16_thSin;
}Trig_Components;

/**
*@briefThisfunctionreturnscosineandsinefunctionsoftheanglefedin
*input
*@paramhAngle:angleinq1.15format(-1~0.9999)
*@retvalTrig_ComponentsCos(angle)andSin(angle)inTrig_Componentsformat
*/
Trig_Componentstrig_functions(int16_thAngle)
{
int32_tshindex;
uint16_tuhindex;

Trig_ComponentsLocal_Components;

/*10bitindexcomputation*/
shindex=((int32_t)32768+(int32_t)hAngle);
uhindex=(uint16_t)shindex;
//uhindex/=(uint16_t)64;
uhindex=uhindex>>6;
/**
|hAngle|angle|std|
|(0,16384]|U0_90|(0,0.5]|
|(16384,32767]|U90_180|(0.5,0.99]|
|(-16384,-1]|U270_360|(0,-0.5]|
|(-16384,-32768]|U180_270|(-0.5,-1)|
*/
//SIN_MASK0x0300u
switch((uint16_t)(uhindex)&SIN_MASK)
{
//0x0200u
caseU0_90:
Local_Components.hSin=
hSin_Cos_Table[(uint8_t)(uhindex)];
Local_Components.hCos=
hSin_Cos_Table[(uint8_t)(0xFFu-(uint8_t)(uhindex))];
break;
//0x0300u
caseU90_180:
Local_Components.hSin=
hSin_Cos_Table[(uint8_t)(0xFFu-(uint8_t)(uhindex))];
Local_Components.hCos=
-hSin_Cos_Table[(uint8_t)(uhindex)];
break;
//0x0000u
caseU180_270:
Local_Components.hSin=
-hSin_Cos_Table[(uint8_t)(uhindex)];
Local_Components.hCos=
-hSin_Cos_Table[(uint8_t)(0xFFu-(uint8_t)(uhindex))];
break;
//0x0100u
caseU270_360:
Local_Components.hSin=
-hSin_Cos_Table[(uint8_t)(0xFFu-(uint8_t)(uhindex))];
Local_Components.hCos=
hSin_Cos_Table[(uint8_t)(uhindex)];
break;
default:
break;
}
return(Local_Components);
}

由于输入的hAngle是Q1.15格式，所以这里可以简单画个图；下面是角度hAngle从0x0000~0xFFFF的示意图，如下所示；

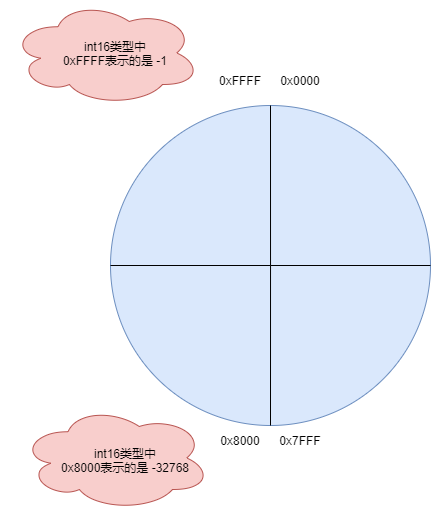
角度值

这里注意，负数是以补码形式进行保存的，正数的补码等于他本身；

负数的补码是除了符号位外，其他位取反，然后加上1；

所以可以算一下 0xFFFF表示-1；

0x8000表示 -32768；

因为Q格式中有无符号的范围和带符号的范围，所以这里的hAngle充分利用这个16 bit的数据，并且兼容了传入参数可以是有符号int16或者是无符号uint16，这里比较绕，先看下面这张图片；

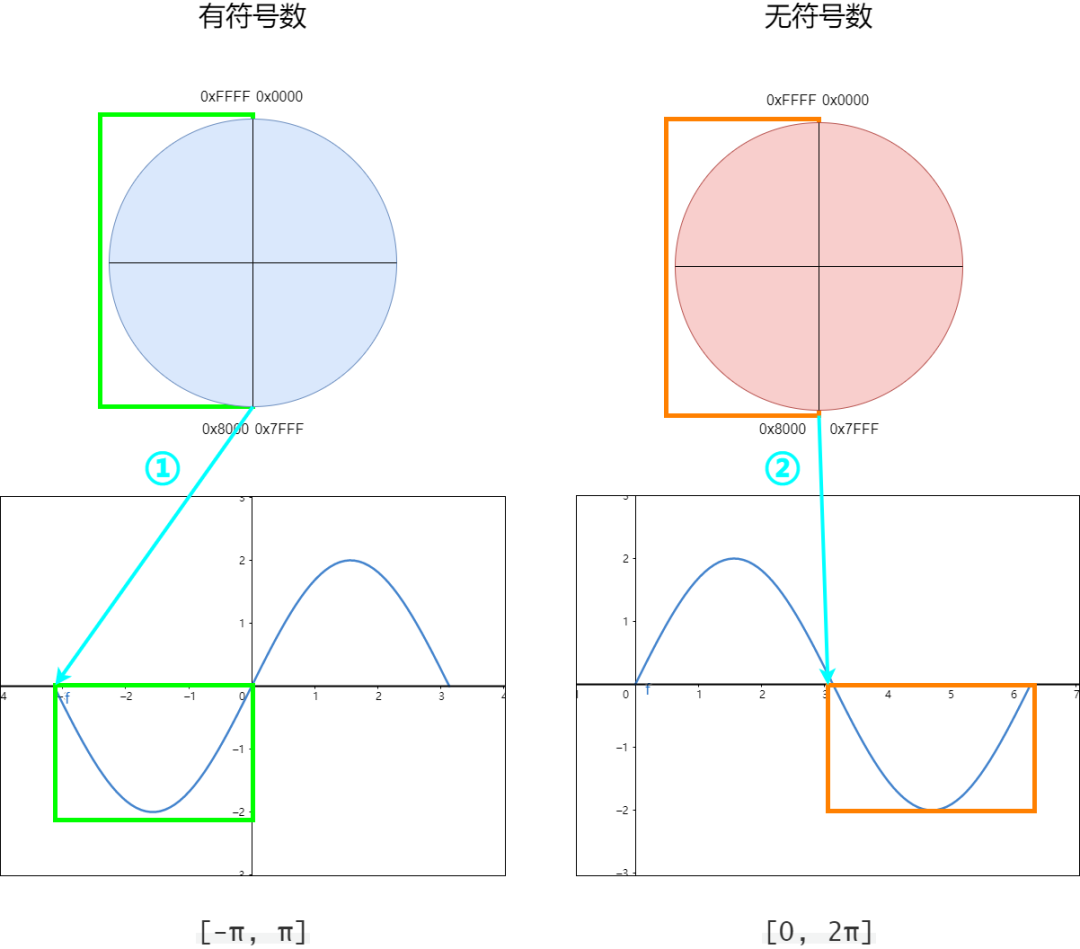
有符号和无符号 对比

上图中；

左边是有符号int16，右边是无符号数uint16；

两个圆形分别表示int16和uint16的数值范围；

左边绿色框内的波形相对应，橙色框内的波形相对应；

这里有几点我们要注意一下，无论是有符号和无符号，他们的周期都是相同的；

有符号整数 int16 ：-32768 ~ 32765 ，

无符号整数 uint16 ：0 ~ 65535，

所以这两者都使用 65536个数来表示正弦的一个周期，也就是 2π。

这里是比较关键的地方，因此对于0x8000 这个关键点，有符号和无符号所表示的数值是不同的；

有符号整数 int16 ：0x8000 表示为 -32768；

无符号整数 uint16 ：0x8000 表示为 32768；

因此这他们刚好相差了一个周期 65536，所以表示的正弦数值y是相同的，正如上图中蓝色箭头①和②所示。

内部实现

由于有符号整数 int16 的最高位是符号位，所以这里我们先把它转化成无符号整形；

前面用 int32类型是为了防止数据溢出，这里加上32768，相当于对正弦波平移了半个周期，所以在下面y和x的映射关系需要根据实际情况来修改；

/*10bitindexcomputation*/
shindex=((int32_t)32768+(int32_t)hAngle);
uhindex=(uint16_t)shindex;
//uhindex/=(uint16_t)64;
uhindex=uhindex>>6;

因为前面提高过正弦表的四分之一是256个数据，所以整个正弦周期应该是 1024 个细分数据，那也就是2的10次，就需要10 bit；

10 bit的数据范围是 0~1023;

16 bit的数据范围是 0~65535;

为了获取有效的高10 bit数据，对数据右移 6 bit，具体如下所示；

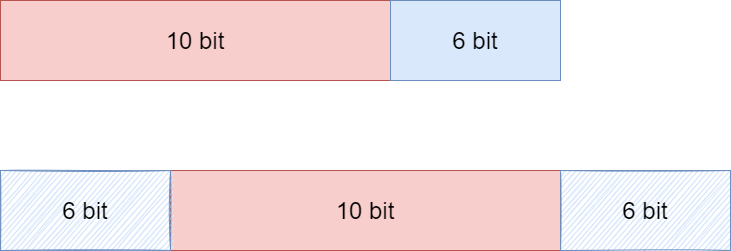
所以，我们又可以得到以下这个数据的范围 0 ~ 1023 ，0 ~ 0x400

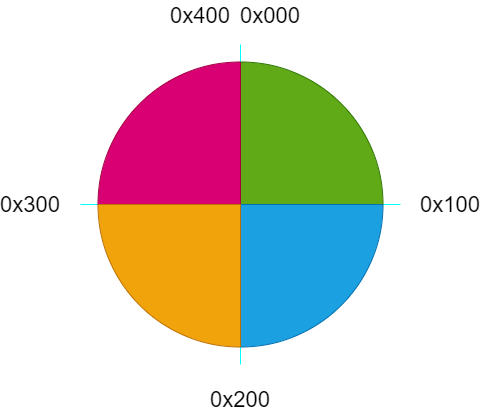
因此我们在程序中引入四个掩码，作为正弦波形落在哪个象限的标识位，这样也避免了使用除法运算，提高了效率，具体如下所示；

#defineSIN_MASK0x0300u
#defineU0_900x0200u
#defineU90_1800x0300u
#defineU180_2700x0000u
#defineU270_3600x0100u

其中，U0_90表示 0° ~ 90°，以此类推；

那为什么是这个映射关系呢？

0~90°不应该是从 0x000u~0x100u吗？这里我们再简单解释一下；

前面有一个这样的操作，具体如下；

shindex=((int32_t)32768+(int32_t)hAngle);
uhindex=(uint16_t)shindex;

这里的hAngle加上32768，相当于加了一个π，正弦波形向左移动了半个周期；因此整体的映射关系要和原始的数据对应起来，具体如下所示；

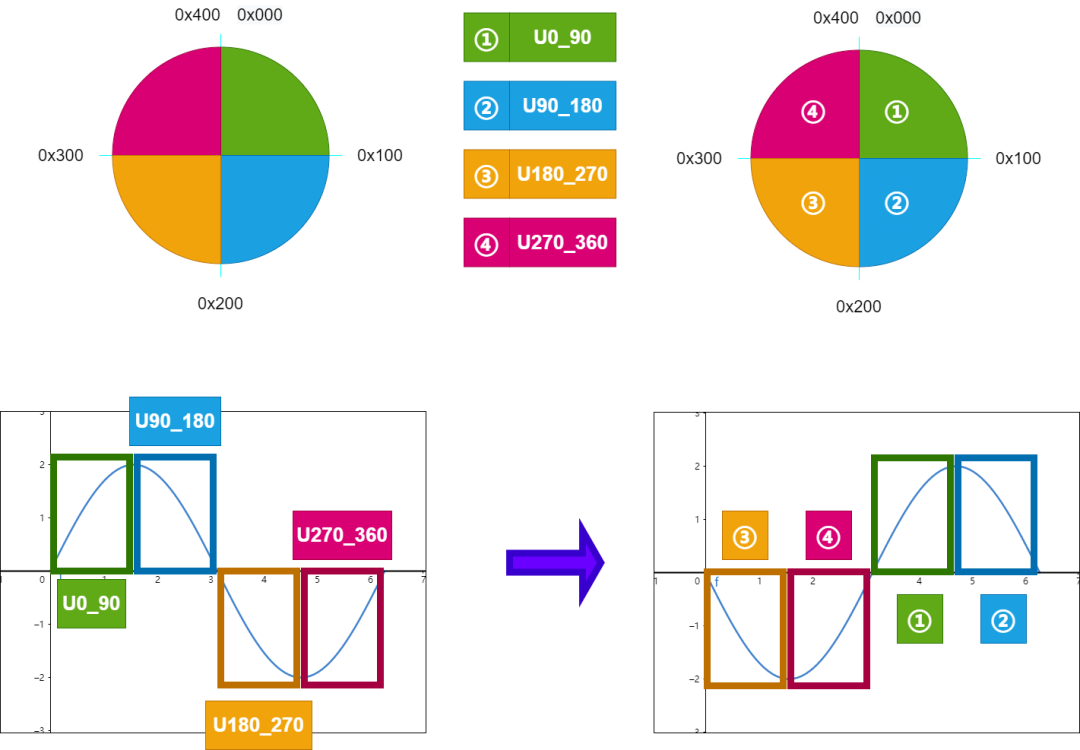
最后，既然我们已经知道波形在哪个象限了，就可以根据当前象限和我们正弦表的关系来得到新的波形，这里有中心对称，关于y轴对称，简单做一下变换就可以得到正弦值和余弦值；

//SIN_MASK0x0300u
switch((uint16_t)(uhindex)&SIN_MASK)
{
//0x0200u
caseU0_90:
Local_Components.hSin=
hSin_Cos_Table[(uint8_t)(uhindex)];
Local_Components.hCos=
hSin_Cos_Table[(uint8_t)(0xFFu-(uint8_t)(uhindex))];
break;
//0x0300u
caseU90_180:
Local_Components.hSin=
hSin_Cos_Table[(uint8_t)(0xFFu-(uint8_t)(uhindex))];
Local_Components.hCos=
-hSin_Cos_Table[(uint8_t)(uhindex)];
break;
//0x0000u
caseU180_270:
Local_Components.hSin=
-hSin_Cos_Table[(uint8_t)(uhindex)];
Local_Components.hCos=
-hSin_Cos_Table[(uint8_t)(0xFFu-(uint8_t)(uhindex))];
break;
//0x0100u
caseU270_360:
Local_Components.hSin=
-hSin_Cos_Table[(uint8_t)(0xFFu-(uint8_t)(uhindex))];
Local_Components.hCos=
hSin_Cos_Table[(uint8_t)(uhindex)];
break;
default:
break;
}

总结

本文简单介绍了正余弦函数的实现，参考了ST的mcsdk中算法，做了简单的分析，其中需要了解一部分Q格式进行定点运算的知识，本文可能存在错误和纰漏，请大家指出。如果大家有更好的方法，欢迎在下方讨论。
审核编辑：黄飞