摩尔定律 VS 功能密度定律
众所周知,随着IC工艺的特征尺寸向5nm、3nm迈进,摩尔定律已经要走到尽头了,那么,有什么定律能接替摩尔定律呢?
这就是我们今天要提出的:“功能密度定律-Function Density Law”,简称“FD Law”。
首先,让我们回顾一下摩尔定律。
1. 摩尔定律
摩尔定律(Moore's Law)是由英特尔(Intel)创始人之一戈登·摩尔(Gordon Moore)于1965年提出来的,至今已有55年。
摩尔定律内容为:当价格不变时,集成电路上可容纳的元器件的数目,约每隔18-24个月便会增加一倍,性能也将提升一倍。换言之,每一美元所能买到的电脑性能,将每隔18-24个月翻一倍以上。
总得来说,摩尔定律有以下三种说法:
1、集成电路芯片上所集成的电路的数目,每隔18-24个月就翻一番。
2、微处理器的性能每隔18-24个月提高一倍,而价格下降一倍。
3、用一个美元所能买到的电脑性能,每隔18-24个月翻两番。
以上几种说法中,以第一种说法最为普遍,第二、三两种说法涉及到价格因素,其实质是一样的。三种说法虽然各有千秋,但在一点上是共同的,即"翻番"的周期都是18-24个月,至于"翻一番"(或两番)的是"集成电路芯片上所集成的电路的数目",是整个"计算机的性能",还是"一个美元所能买到的性能"就见仁见智了。
这一定律揭示了信息威廉希尔官方网站 进步的速度,尽管这种趋势已经持续了超过半个世纪,摩尔定律仍应该被认为是观测或推测,而不是一个物理或自然法。
摩尔定律到底准不准?让我们先来看下面一张图,从图中可以看出,采样点基本位于曲线的附近,可以看出摩尔定律基本上还是准确的。
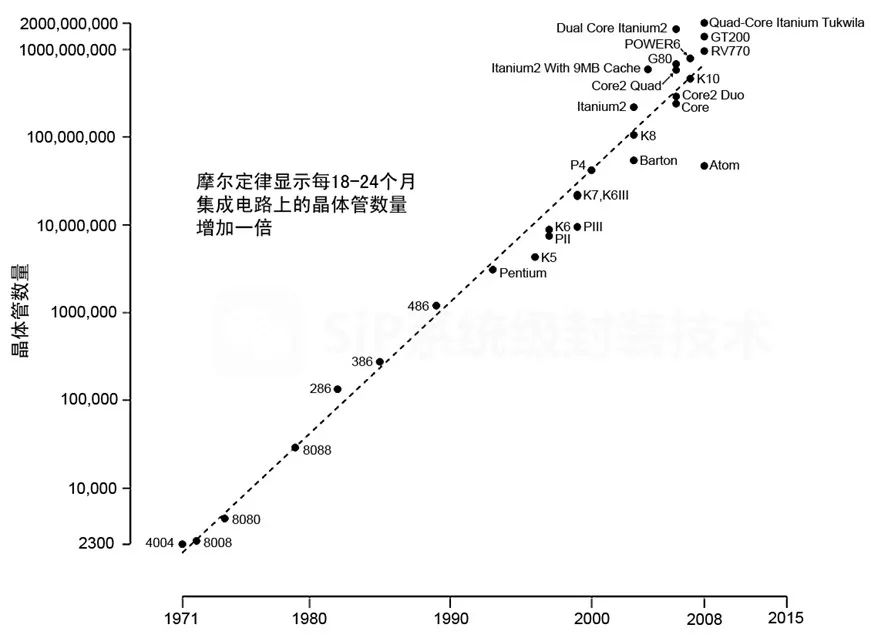
摩尔定律并非数学或者物理定律,而是对发展趋势的一种预测,因此,无论是文字表述还是定量计算,都应当容许一定的宽裕度。从这个意义上看,摩尔的预言是相当准确了,所以才会被业界人士的公认,并产生巨大的反响。
"摩尔定律"的终结
摩尔定律问世至今已55年了,我们知道:芯片上元件的几何尺寸总不可能无限制地缩小下去,这就意味着,总有一天,芯片单位面积上可集成的元件数量会达到极限。
从威廉希尔官方网站 的角度看,随着硅片上线路密度的增加,其复杂性和差错率也将呈指数增长,同时也使全面而彻底的芯片测试几乎成为不可能。
一旦芯片上特征尺寸达到1纳米时,相当于只有5个硅原子的大小,这种情况下材料的物理、化学性能将发生质的变化,致使采用现行工艺的半导体器件不能正常工作,摩尔定律也就要走到它的尽头了。
2. 功能密度定律
既然摩尔定律已经要走到尽头了,就需要有一个新的定律来接替摩尔定律,有什么定律能接替摩尔定律呢?
这就是我们今天要提出的:“功能密度定律”(Function Density Law)。
功能密度定律:对于所有的电子系统来说,沿着时间轴,系统空间内的功能密度总是在持续不断地增大,并且会一直持续下去。
Function Density Law:For all electronic systems, along the time axis, the function density in system space is constantly increasing and will continue.
下图为功能密度定律的曲线描述:
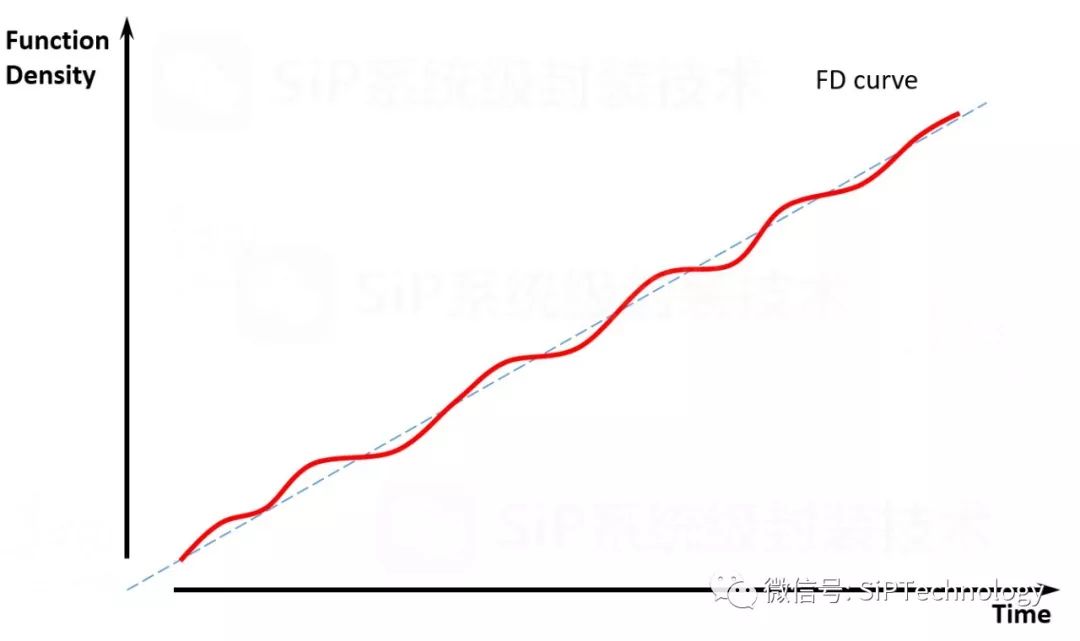
从以上曲线可以看出,电子系统的功能密度会随着时间延续而持续地增长,其增长的快慢在不同的历史时期会有所不同,如果有新的威廉希尔官方网站 的突破,其增长的就会比较快,如果没有新威廉希尔官方网站 突破,其增长则会比较缓慢,但总的趋势是不断增长。
要理解功能密度定律,首先我们要理解什么是功能密度?
功能密度:单位体积内包含的功能单位的数量称为功能密度。
Function density: The number of Function UNITs contained in a unit volume is called function density.
功能密度中的关键词是功能单位,那什么又是功能单位(Function UNITs)呢?我们需要了解一下电子系统的6级功能分类。
电子系统6级分类法:
6-levels classification of electric system:
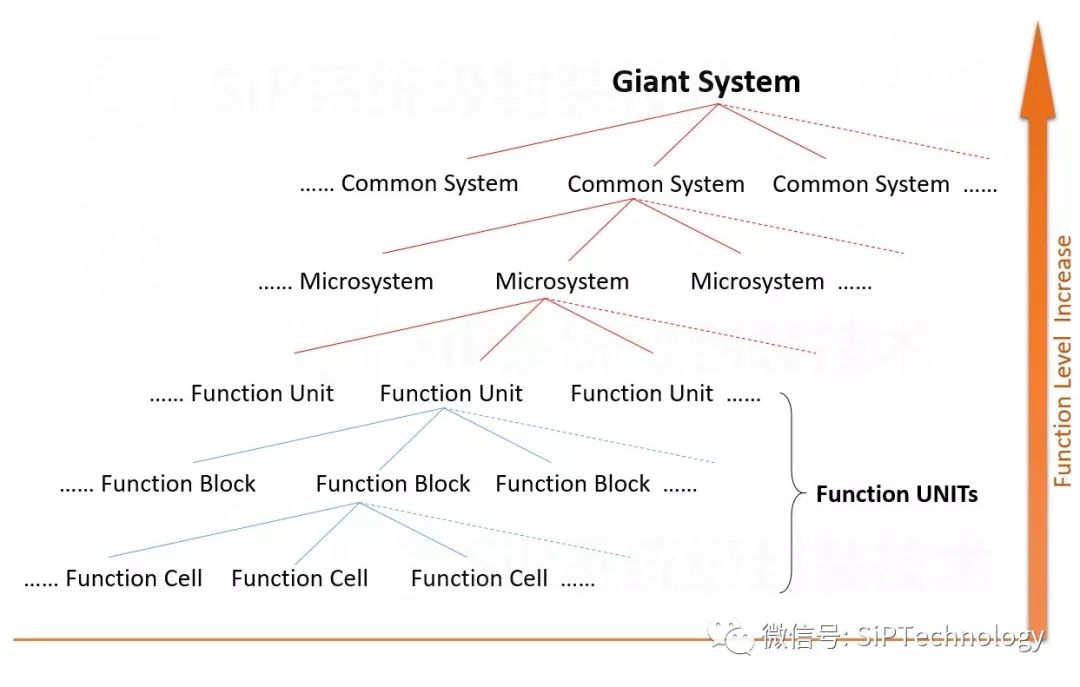
功能细胞,Function cell(FC),功能细胞是电子系统组成的最小功能单位,不可拆分,如果拆分,功能则会丧失,不可恢复,例如晶体管Transistor,电阻、电容、电感等都是功能细胞。
功能块,Function block(FB),功能块由功能细胞组成,具有一定的逻辑功能,例如,6个Transistor可以组成一个SRAM存储功能块,1个Transistor和1个电容可以以组成一个DRAM存储功能块,4个MOS管可以组成一个与非门或者或非门。功能块是具有特定功能的功能单位。
功能单元,Function unit(FU),功能单元由功能块组成,可以完成复杂功能的功能单位,例如算术逻辑单元(ALU),输入输出控制单元(IO Control Unit),中央处理单元(CPU)等,计算机的处理器,DSP,FPGA,存储器等都可以归属于功能单元这一级别的功能单位。
微系统,Micro System(MS),到这一级别,我们开始定义系统的概念,微系统可以独立完成系统功能,并且体积较小,通常并不直接和最终用户打交道,例如SiP, SoC,SoP等,微系统通常可由功能单元、功能块或者功能细胞组成。
常系统,Common System(CS),也可称之为常规系统,顾名思义就是常人能接触到的系统,一般是指和最终用户直接打交道的系统,这里的最终用户指的是人。例如手机,电脑,家用电器等都可称为常系统,常系统通常由微系统、功能单元组成;
大系统,Giant System(GS),一般是指复杂而庞大的系统,例如无线通信网络系统,互联网系统,载入航天系统、空间站系统等,大系统通常由常系统、微系统等组成。
在以上的定义中,功能细胞(FC),功能块(FB),功能单元(FU),都可以称之为功能单位(FUs),它们分别属于不同级别的功能单位。
我们再回顾一下功能密度的定义:
单位体积内包含的功能单位的数量称为功能密度。这其中的功能单位(Function UNITs)可以是:功能块(Function Block),功能细胞(Function Cell)或者功能单元(Function Unit)。
需要读者注意的是:在进行同一类型系统的功能密度比较时,需要采用相同级别的功能密度定义。例如,系统A、B、C的功能密度进行比较,A采用功能块(Function Block)作为功能单位来定义功能密度,则B和C同样需要采用功能块(Function Block)作为功能单位来定义功能密度。
3. 功能密度定律的意义
如果将功能密度定义中的功能单位具体为功能细胞(Transistor),并将其空间二维化,将其时间具体化,那么,功能密度定律就会缩化为摩尔定律。
如果将集成电路上的晶体管集成从二维平面扩展为三维空间,将晶体管扩展为功能单位,并将时间由具体变为趋势化,那么,摩尔定律就会扩展为功能密度定律。
我们也可以这么理解,对于电子系统的集成来说,摩尔定律是功能密度定律的在集成电路上特例,而功能密度定律则是摩尔定律在整个电子系统的扩展。
也许会有人问,为什么功能密度定义时用的不是确定的功能单位,而是三个层次的功能单位(功能块FB,功能细胞FC,功能单元FU)呢?这是由于功能本身的复杂性和不确定性。
例如,新威廉希尔官方网站 的发展,功能块的结构发生了进化,仅需要更小的功能块(Function Block) 就可以实现同样的功能,这样,即使最底层的功能细胞(Function Cell)Transistor的数量没有变化,其功能密度也同样是增加的。
比如我们通常用的SRAM需要6个晶体管(Transistor)可以实现一个存储单元,称为6T,一种新威廉希尔官方网站 的出现据说可以用1个晶体管实现一个存储单元,称为1T,这样,即使单位体积内的晶体管数量不变,其功能密度却增加了6倍。
以此类推......
4. 小结和展望
功能密度定律预测了电子系统集成的趋势,并将成为判断电子系统先进性的重要指标!
摩尔定律是关于人类创造力的定律,实际上是关于人类信念的定律,当人们相信某件事情一定能做到时,就会努力去实现它。摩尔当初提出他的观察报告时,实际上是给了人们一种信念,使大家相信他预言的趋势一定会持续。
功能密度定律同样是关于人类创造力的定律,也是关于人类信念的定律,当人们相信电子系统空间内的功能密度一定能会持续增加时,同样会努力去实现。
功能密度定律(Function Density Law,简称FD Law)是作者Suny Li(Li Yang)于2020年1月20号在本文中首次正式提出。
在此之前,作者经历了20年的电子系统设计,积累了丰富的项目经验,并且通过了长久的分析和思考而得出。
功能密度定律(FD Law)会不会像摩尔定律(Moore's Law)一样,成为电子系统集成的最重要定律呢?
现在,我们还不急着给出定论,等十年以后的2030年我们再看吧!
不再纠结于二维平面尺度上晶体管的缩放,而把思维投入到更广阔的空间,从多维度的集成,从结构化的创新,从更灵活的尺度去评判,去发展!
理解并运用功能密度定律,你就不会再纠结摩尔定律的终结,因为新的空间已经为我们打开,并且更为广阔!
正如人们常说的:“山重水复疑无路,柳暗花明又一村!”
审核编辑:刘清
-
摩尔定律
+关注
关注
4文章
633浏览量
78971 -
IC工艺
+关注
关注
0文章
4浏览量
5916
原文标题:摩尔定律 vs 功能密度定律
文章出处:【微信号:bdtdsj,微信公众号:中科院半导体所】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
晶圆和摩尔定律有什么关系?
摩尔定律也适用于EPON芯片商用之路?
半导体行业的里程碑“摩尔定律”竟是这样来的
摩尔定律推动了整个半导体行业的变革
IC芯片的密度和计算机的速度能够一直按照摩尔定律前行吗?
摩尔定律,摩尔定律是什么意思
摩尔定律的历程





 功能密度定律是否能替代摩尔定律?摩尔定律和功能密度定律比较
功能密度定律是否能替代摩尔定律?摩尔定律和功能密度定律比较












评论