协方差矩阵是统计学中常用的工具,用于描述多个随机变量之间的关系。在进行数据分析和建模时,协方差矩阵能够提供重要的信息,帮助我们理解变量之间的线性关系,以及它们的方差。本文将详细介绍协方差矩阵的各个元素的含义,并解释协方差矩阵的计算方法。
首先,我们来了解一下协方差的基本概念。协方差是用来衡量两个变量之间的相关性的指标。数学上,给定两个随机变量X和Y,它们的协方差定义为:
cov(X,Y) = E[(X - E(X))(Y - E(Y))]
其中,cov(X,Y)表示变量X和Y的协方差,E(X)和E(Y)分别表示X和Y的期望(即均值)。协方差描述了X和Y之间的线性相关程度。如果协方差为正数,说明X和Y呈正相关;如果协方差为负数,说明X和Y呈负相关;而如果协方差接近于零,说明X和Y之间基本没有线性关系。
协方差矩阵是一个方阵,每个元素表示两个变量之间的协方差。对于n个随机变量X1, X2, ..., Xn,它们的协方差矩阵C定义为:
C = [cov(Xi, Xj)]
其中,C是一个n×n的矩阵,cov(Xi, Xj)表示变量Xi和Xj的协方差。协方差矩阵提供了关于变量之间线性相关性的完整信息,通过分析协方差矩阵,我们可以了解变量之间的关系,并进一步进行数据建模和预测。
协方差矩阵的元素可以分为两类:对角线元素和非对角线元素。对角线元素表示自己和自己的协方差,即cov(Xi,Xi),它等于变量Xi的方差。方差是衡量一个变量离散程度的指标,如果一个变量的方差较大,说明它的取值较为分散;相反,如果一个变量的方差较小,说明它的取值集中在均值附近。
非对角线元素表示两个不同变量之间的协方差,即cov(Xi,Xj)。协方差的绝对值表示两个变量之间的线性关系的强度,而符号表示关系的方向。如果协方差为正数,说明两个变量呈正相关;如果协方差为负数,说明两个变量呈负相关;而如果协方差接近于零,说明两个变量之间基本没有线性关系。
协方差矩阵的计算方法有多种,最常用的是样本协方差矩阵的计算方法。给定一个包含n个样本的数据集,每个样本有m个变量的取值,我们可以根据以下公式计算协方差矩阵的估计值:
C = 1/(n-1) × [Σ(xi - x̄)(xi - x̄)ᵀ]
其中,C表示协方差矩阵,n表示样本个数,xi表示第i个样本,x̄表示所有样本的均值向量,(xi - x̄)表示样本xi与均值向量的差值,(xi - x̄)ᵀ表示差值的转置。
通过计算样本协方差矩阵,我们可以得到关于变量之间线性相关性的估计值。协方差矩阵越接近于零矩阵,说明变量之间线性相关性越弱;而协方差矩阵的非零元素越大,说明变量之间线性相关性越强。
在实际应用中,协方差矩阵被广泛应用于数据分析、金融风险测度、机器学习等领域。通过分析协方差矩阵,我们可以识别出变量之间的主要相关性、剔除无关变量、构建特征向量等。此外,协方差矩阵还可以用于生成随机变量和interwetten与威廉的赔率体系 数据等。
综上所述,协方差矩阵是一个重要的统计工具,用于描述多个变量之间的线性相关关系。它的各个元素分别表示变量之间的自协方差和协方差,通过分析协方差矩阵,我们可以获得关于变量之间线性相关性的重要信息,并进一步进行数据建模和预测。计算协方差矩阵的方法有多种,其中样本协方差矩阵是最常用的估计方法。
-
线性
+关注
关注
0文章
198浏览量
25147 -
协方差矩阵
+关注
关注
0文章
5浏览量
6039 -
机器学习
+关注
关注
66文章
8408浏览量
132573 -
数据分析
+关注
关注
2文章
1446浏览量
34051
发布评论请先 登录
相关推荐
Matlab协方差矩阵的计算原理
Matlab协方差矩阵的计算原理
基于协方差矩阵的CFA插值盲检测方法
基于协方差矩阵特征分解的多通道SAR-GMTI方法及性能分析
基于杂波协方差矩阵特征向量分析STAP降维方法
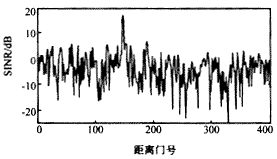
基于稀疏干扰协方差矩阵重构的稳健自适应波束形成算法(CAPON谱改正)
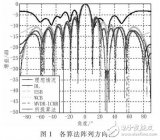
协方差公式_协方差的计算公式例子

协方差矩阵是什么_协方差矩阵计算公式_如何计算协方差矩阵

基于协方差矩阵降维稀疏表示的二维波达方向估计方法
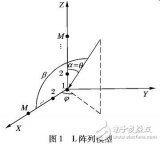
基于协方差矩变异系数的能量泄露评估模型





 协方差矩阵中各元素含义 协方差矩阵怎么算
协方差矩阵中各元素含义 协方差矩阵怎么算










评论