上期我们讲了槽内线圈的感应电势,解答了用“Blv观点”计算槽内线圈感应电势的有关问题,明确了电机线圈中的感应电势大小与电枢开槽无关,“Blv观点”不仅适用于计算光滑电枢表面的线圈感应电势,而且也适用于计算电枢开槽后槽内线圈感应电势的计算,但用“Blv观点”计算槽内线圈的感应电势时,其中的B必须用光滑电枢时的气隙磁密值代入。
与此问题类似,通电导体在磁场中会受到的电磁力的作用,电磁力的大小可用“BIL”计算。具体到电机中,如果电枢是光滑的,线圈位于光滑电枢表面,则用“BIL观点”计算线圈导体的受力,进而计算电磁转矩是非常容易理解的;如果电枢开槽,线圈的导体位于槽内,同样存在着槽内的磁密很小,“BIL观点”还是否适用的问题。如果能用,其中的B又应该用何值代入?另外同学们还经常问到一个问题,就是槽内线圈产生的电磁力是作用在槽内的导体上还是作用在铁芯上?本期就来回答这些问题!
1 磁介质在磁场中受到的磁场力
将一块磁介质(简称“磁质”)置于磁场中,就会受到磁场力的作用。在磁质的某点附近取一体积微元dV,设该体积微元所受到的磁力为dF,则定义dF/dV为该点磁质所受到的体积磁力密度,即f=dF/dV。也就是说,磁质上某点的磁力密度就是该点附近单位体积的磁质所受到的磁场力。根据相关电磁理论,磁质在磁场中所受到的体积磁力密度为:
f=J×B-(1/2)H²•gradμ+f″ ⑴
需要说明的是,上式为不失一般性的磁力密度表达式,全面考虑到了各种情况:其中第一项是考虑了磁质中包含传导电流所受到的磁场力,即通电导体在磁场中受到的磁力,也就是人们常说的“洛伦兹力”,式中:J为该点处的传导电流密度矢量;B为该点处的磁密矢量,该项表明通电导体在磁场中所受到的磁力密度为电流密度矢量与磁密矢量的叉乘,进一步推导(略)可知,如果电流方向与磁场方向垂直,则该项磁力的大小就等于BIL,作用点在载流导体上,方向可用左手定则判定;第二项是考虑了磁质中各点的磁导率分布可能不同,式中:gradμ为该点磁导率的梯度;H为该点的磁场强度,该项表明当磁质内各点的磁导率分布不均匀时,就会因各向磁阻不均匀而产生的磁力,称为麦克斯韦力,麦克斯韦力的大小与该处磁导率的梯度成正比,该项前面的负号“-”表示麦克斯韦力的方向为从μ值大处指向μ值小处;第三项 f″则表示磁质在磁场中受到应力后发生变形,于是各方向的μ值发生变化而引起的力,称为磁致伸缩力,通常在磁质内部 f″会被材料局部的弹力相平衡,属于内力,只影响磁质内部的应力分布,不影响整个磁质所受到的总合力,加之在简化的铁磁物质模型中,认为磁质变形时μ并不随之而变化,因此通常在电机中将该项忽略不计。这样在分析实际电机中的电磁力时,就只考虑前面两项——洛伦兹力和麦克斯韦力,并还可根据电机磁路的具体情况,作相应的简化。
整块磁质所受到的磁场力:
F=∭【V】f•dV⑵
式中:【V】为积分区域,即整个磁质的体积。
2 磁场通过两种不同磁介质时交界面上的磁场力
对于⑴式中的第二项——麦克斯韦力,若一种磁质内部的μ为常数(处处相等),则该磁质内部gradμ=0,这就意味着同一磁介质内部的麦克斯韦力为0,但如果磁路中存在两种磁介质,例如电机的磁路中就存在铁心与空气两种磁介质,由于铁心与空气的磁导率相差巨大,那么在铁心与空气的交界面上就存在巨大的法向磁导率梯度gradμ,因此在交界面上就会产生巨大的麦克斯韦力。因此在分析电机中的电磁力时,往往不考虑铁心内部的体积磁力密度,而只考虑两种不同介质交界面上的面积磁力密度,即磁应力,为此⑵式可写作:
F=∭【V】f•dV=∬【A】σ•da⑶
式中:【A】为积分区域,即为包围体积【V】的闭合曲面;σ为磁应力,即单位面积上的电磁力;da为曲面A上的面积微元。
根据麦克斯韦张量理论,经过一系列复杂的推导(略),得出两种不同磁介质交界面上的磁应力:
σ=(1/2μ)(Bn²-Bt²)n+(1/μ)Bn•Bt•t=σn+σt ⑷
式中:Bn和Bt分别为交界面上法向和切向的磁密;n和t分别代表交界面上的单位法向矢量和单位切向矢量;σn和σt分别为交界面上磁应力的法向分量和切向分量:
σn=(1/2μ)(Bn²-Bt²)
σt=(1/μ)Bn•Bt ⑸
3 铁心和空气交界面的磁场力
如图1所示表示铁心和空气形成交界面A。设空气为介质1,μ1=μ0,空气侧的磁密为B1;铁心为介质2,μ2=μFe,铁心侧的磁密为B2;磁场为二维平行平面场。
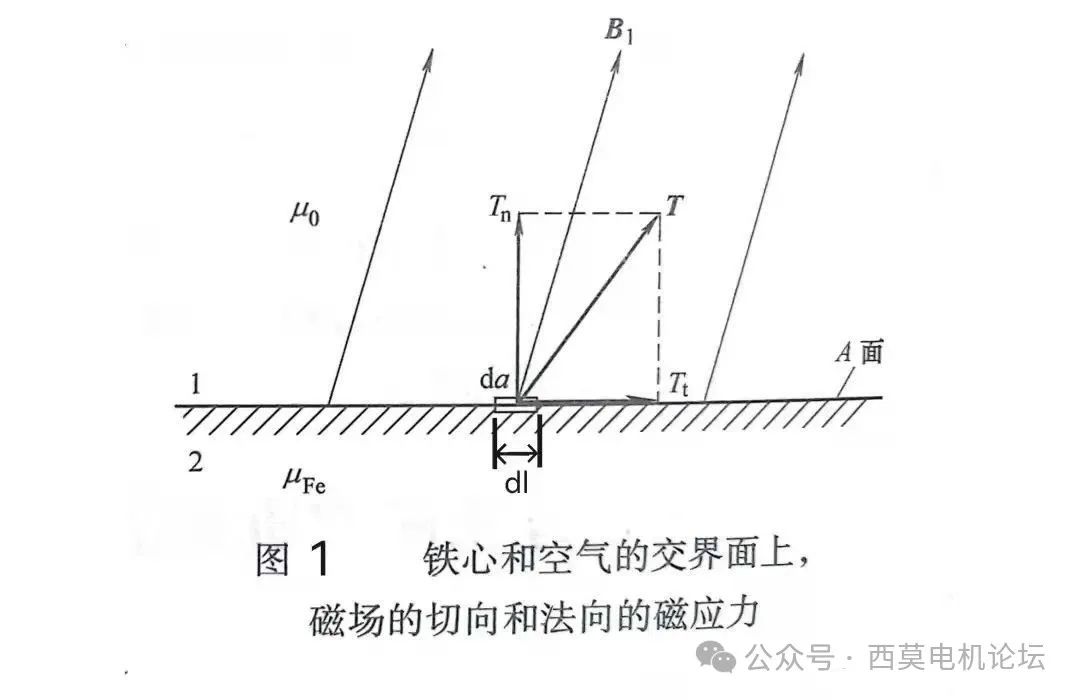
在交界面A上取一面积微元da,根据⑸式,空气侧磁应力的切向分量σ1t和法向分量σ1n分别为:
σ1t=(1/μ0)B1n•B1t
σ1n=(1/2μ0)(B1n²-B1t²) ⑹
铁心侧磁应力的切向分量和σ2t和法向分量σ2n分别为:
σ2t=(1/μFe)B2n•B2t
σ2n=(1/2μFe)(B2n²-B2t²) ⑺
于是作用在微元面积da上的合成切向磁应力σt和法向磁应力σn分别为:
σt=σ1t-σ2t=(1/μ0)B1n•B1t-(1/μFe)B2n•B2t
σn=σ1n-σ2n=(1/2μ0)(B1n²-B1t²)-(1/2μFe)(B2n²-B2t²) ⑻
若交界面上无电流层,则交界面上的边界条件为:
B1n=B2n=Bn≈Bδ
H1t=H2t=Ht ⑼
式中:Bδ为气隙磁密。
将⑼式代入⑻式得:
σt=0
σn=[(μFe-μ0)/(2μFe•μ0)]•(Bn²+μFe•μ0•Ht²) ⑽
由⑽式可见,当交界面上无电流层时,交界面上仅有法向磁应力,其方向为从铁心指向空气,切向应力恒等于0。由于铁心的磁导率远大于空气的磁导率,即μFe>>μ0,故认为磁力线进入铁心时,基本上垂直于铁心表面,即Ht≈0,于是法向磁应力可近似写成:
σn≈Bn²/(2μ0)≈Bδ²/(2μ0) (11)
通常工程实践中,都是用(11)式来计算法向磁应力的。
4 线圈置于光滑电枢表面时的切向力
在实际电机中,如果把图1中的铁心侧看作光滑的电枢铁心;空气侧看作气隙;把电枢绕组看作均匀分布在电枢铁心与气隙的交界面上,电枢绕组中的电流看作是均匀分布在交界面上没有厚度的电流层。那么在电机空载时,交界面上没有电流层,根据上述第3章的分析,分界面上的切向磁应力和法向磁应力即由(10)式决定,也就是说,光滑电枢的电机空载时切向磁应力为0,只有法向磁应力,法向磁应力近似按(11)式计算。由于法向磁应力不产生电磁转矩,而产生电磁转矩的切向磁应力为0,因此空载时电磁转矩为0。
负载时,电枢绕组中通有电流,即交界面上存在电流层有,设电枢圆周单位弧长上的电流为A′(即电机设计里的线负荷,为了区别于交界面A,这里用A′代表线负荷):
A′=∑I/(2πR) (12)
式中:∑I为整个电枢圆周上的总电流,即各相电流的安导总和;R为电枢半径。
接下来分析交界面上存在电流层时的边界条件。首先看法向边界条件,由于磁力线是不间断的闭合曲线,因此在交界面上,铁心和气隙两侧的法向磁密相等,即交界面上的法向边界条件仍然是B1n=B2n=Bn≈Bδ,交界面上的法向磁应力仍然按(11)式计算。
再看切向边界条件,图1中将磁场强度H沿包围面积微元da的闭合曲线周长积分就应该等于da面积内所包围的电流,即:
H1t•dl+H2t•dl=A′•dl (13)
式中:H1t、H2t分别为分界面上空气和铁心侧磁场强度的切向分量;dl为电枢圆周上的弧长微元。考虑到铁心中的磁导率远大于空气的磁导率,即μFe>>μ0,因此铁心侧的切向磁压降可以忽略不计,认为所有磁压降全部降在气隙侧,即H2t•dl=0,H2t=0,于是有H1t=A′。因此交界面上的边界条件为:
B1n=B2n=Bn≈Bδ
H1t=A′}(14)
H2t=0
将上述法向和切向边界条件代入⑻式的第一个公式,得负载时切向磁应力为:
σt=(1/μ0)B1n•B1t
=B1n•H1t
=Bδ• A′ (15)
由(15) 式可见,电枢表面的切向磁应力就是电机设计里所说的电磁负荷!
进一步推导电机负载时总的切向力为:
Ft=σt•2πR•L
=Bδ•A′•2πR•L
=Bδ•∑I•L (16)
式中:L为铁心有效长度。由(16)式可见,光滑电枢表面的电机,负载时的切向电磁力就是“BIL”。
小结一下:线圈置于光滑电枢表面时,空载切向磁应力为0,法向磁应力约为Bδ²/(2μ0),电磁转矩为0;负载时的法向磁应力仍约为Bδ²/(2μ0),切向磁应力等于负载时的电磁负荷,切向电磁力可以用 “BIL观点”来计算,切向电磁力的作用点是作用在线圈导体上,铁心表面只受法向电磁力作用。
5 线圈置于电枢槽内时的切向力
当电枢开槽、导体嵌入槽内以后,情况有了很大的变化。由于铁心的磁导率远大于空气的磁导率,槽内磁通密度相对较低,因此载流导体放入槽内后,导体上所受到的电磁力将急剧下降,此时切向磁场力和由此产生的电磁转矩,大部份将集中在电枢齿壁上。下面用磁应力来说明此问题。
如图2a)表示空载时主极所产生的气隙和槽内磁场,图b表示槽内载流导体单独作用(不考虑主极磁场)时,槽内和气隙中的磁场。设铁心的磁导率μFe=常值,把图2a)和图2b)两个磁场叠加,可得负载时气隙和槽内的合成磁场,如图2c)所示。
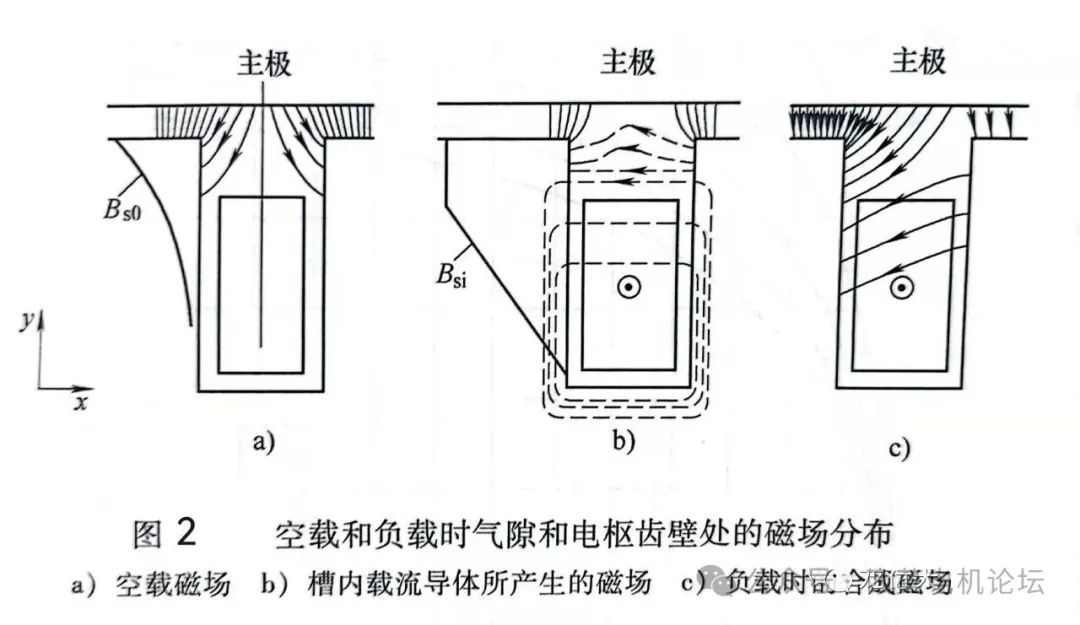
比较图2a)和图2c)可以看出:空载时电枢左、右齿壁上的磁场为对称分布,作用在左、右齿壁上的法向(x方向)磁场力互相平衡,使切向合成磁场力和相应的电磁转矩为0。负载时,由于载流导体的作用,气隙和槽内的磁场发生畸变,左、右齿壁上的磁场分布不再对称,左齿壁上的磁场加强、磁应力加大,右齿壁上的磁场减弱、磁应力减小,结果使齿上受到一个x方向(即切向)的磁场力和电磁转矩。
设Bs0为空载时齿壁上的磁通密度,Bsi为槽内载流导体单独作用时,在左、右齿壁处所产生的磁通密度;则负载时左齿壁上的磁通密度Bs1=Bs0+Bsi,右齿壁上的磁通密度Bs2=Bs0-Bsi,如图2c)所示;于是由式(11)可知,作用于左、右齿壁上的合成磁应力σ为:
σ≈(1/2μ0)(Bs1²-Bs2²)
=(1/2μ0)(Bs1+Bs2)(Bs1-Bs2)
=(1/2μ0)•2Bs0•2Bsi
=(2/μ0)Bs0•Bsi (17)
合成磁场力F则为
F=∫【0,h】σ•L dy=(2/μ0)L∫【0,h】Bs0Bsidy (18)
式中:h为槽高;L为铁心有效长度。此力对齿壁而言是法向力,对电枢而言,则是产生电磁转矩的切向力。
一般情况下,要用解析法来推导出Bs0和Bsi是极为困难的。但是,对于矩形开口槽、且槽形很深(认为h→∞),载流导体置于槽底的情况,可以用保角变换法来求出槽壁处的Bs0和Bsi,并由此算出作用在载流导体上的合成的磁场力F。对于这种特定情况,经过一系列复杂的推导和计算(略)可得到如下结论:
①当槽深h→∞时,作用在左、右齿壁上的合成磁场力大小,恰好等于电枢为光滑时作用在载流导体上的切向电磁力F0,F0=BδIL,其中Bδ为光滑电枢时的空载气隙磁密。
②从槽口到深度d处,齿壁上的合成磁场力Fd如图3所示。
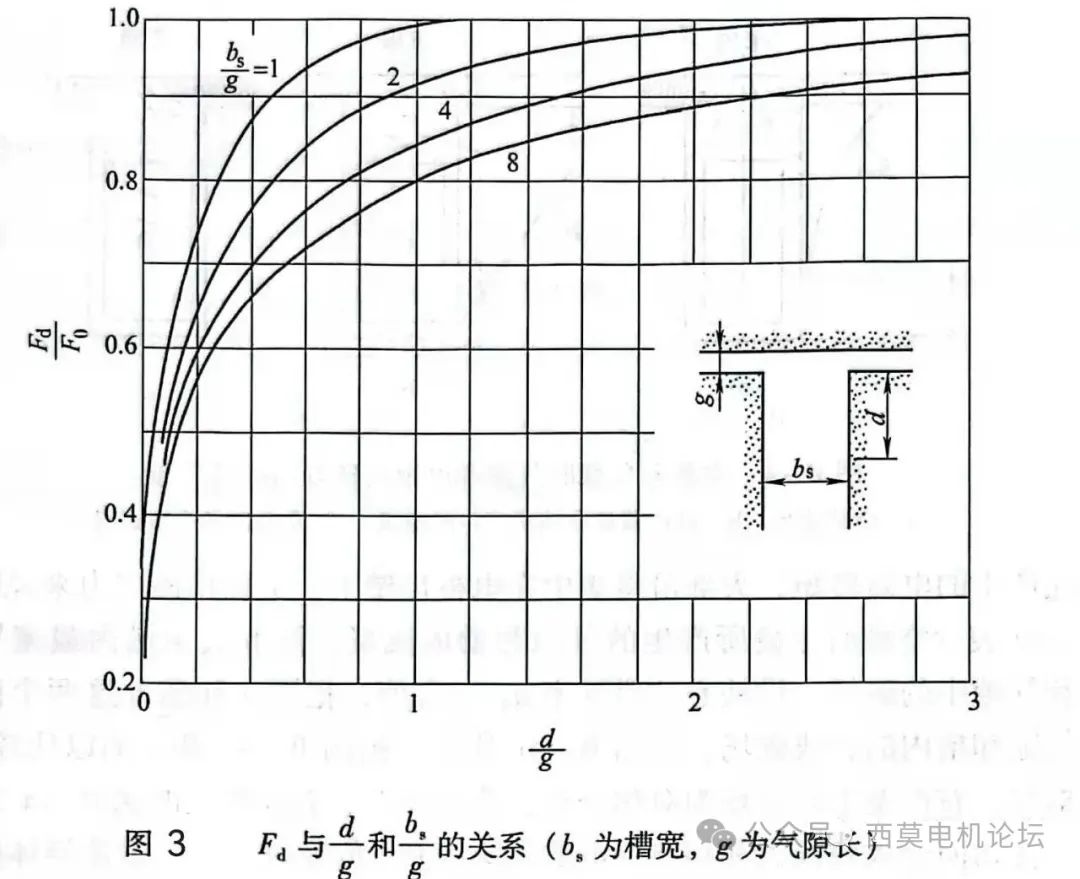
由图可见,90%以上的磁场力将集中在离槽口2.5g深(g为气隙长)的齿壁上。
③当载流导体进入槽内时,由于齿的屏蔽作用,导体上所受到的切向电磁力将随导体所处深度的增大而急骤下降。例如当bs/g=4、载流导体为线电流、进入槽内深度d=2g时,作用在导体上的切向电磁力,将下降到置于光滑电枢表面时的10%左右。
用上述磁应力法来计算磁场力,其优点是既可算出实际磁场力的分布,又可算出总的电磁力和电磁转矩;缺点是需要求出负载时整个电机内的磁场分布,这用解析法是不可能做到的,只能通过数值计算的办法才能做到。
必须强调一个重要结论:电枢开槽后,无论何种槽型,作用在电枢齿壁上的合成切向磁场力,与作用在槽内载流导体上的切向电磁力两者之和,恒等于载流导体置于光滑电枢表面时的切向电磁力“BIL”,这就意味着电枢开槽后,仍然可以用“BIL观点”来计算切向电磁力!特别是如果仅需知道总的电磁转矩,而无需得知电磁力和电磁转矩的分布时,就可以作为载流导体置于光滑电枢表面的情况来处理,并用“BIL观点”算出电磁力和总的电磁转矩。但必须注意以下两点:一是此时电枢表面必须是光滑的圆柱面,否则将导致错误的结果;二是这样处理虽然总的切向电磁力和电磁转矩结果是正确的,但是并未揭示问题的实质和切向电磁力的分布情况,实际上电枢开槽后,产生电磁转矩的切向力主要是作用在铁心的齿上,而槽内载流导体受到的切向力很小,通常可以忽略不计。
其实上述重要结论还可从另外一个角度,用“虚位移法”来理解和解释:假设载流导体为“线电流”,即槽的面积远大于载流导体截面积,导体的粗细可以忽略,认为载流导体是一根无限细的导线,当把该载流导体放入很深的槽底时,则电机内部的磁场分布(气隙和槽内的磁场分布)就与导体在槽底的切向位置无关,将载流导体在槽底切向移动位置时并不影响槽内和气隙磁场的分布,因而磁场的储能不会因导体在槽底作切向位移而变化,这就意味着磁场储能对导体切向位移的偏导数为0,说明导体所受到的切向电磁力即为0。而铁心若沿切向位移一个很小的角度时,磁场的储能会变化很大,即磁场储能对铁心切向位移的偏导数很大,说明切向电磁力主要作用在铁心上。当然上述这种分析是建立在理想的假设条件下,如:“线电流”模型、槽子足够窄而深、导体位于槽内足够深处等,如果考虑到实际电机中槽子深度有限、导体离槽口较近等因素,则槽内载流导体也会受到一定的切向电磁力,特别是当槽子宽而浅、导体离槽口很近时,导体受到的电磁力会有所增大(如图3所示),但与齿壁受到的切向力相比,导体受到的切向电磁力还是很小,可以忽略的。
总结一下:
①电枢表面光滑时,电枢受到的切向电磁力可以用“BIL观点”来计算,切向电磁力的作用点是作用在载流导体上。因此在设计无槽电机时,要特别注意绕组与电枢铁心之间的机械固定问题,必须要有足够的附着力,以防线圈与铁心之间扭脱打滑发生相对移位。
②电枢开槽后,线圈导体嵌放于槽内,此时仍然可以用“BIL观点”来计算总的切向电磁力的大小,但切向电磁力的作用点并不是作用在导体上,而是主要作用在铁心的齿壁上,而槽内载流导体上的切向电磁力可以忽略不计。因此,设计有槽电机时,应该对齿根部位进行必要的机械强度校核,以免齿根断裂。
审核编辑:刘清
-
电磁力
+关注
关注
1文章
78浏览量
14260 -
电机绕组
+关注
关注
0文章
68浏览量
10617 -
电磁转矩
+关注
关注
0文章
55浏览量
8672
原文标题:电机绕组(十九)
文章出处:【微信号:西莫电机论坛,微信公众号:西莫电机论坛】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐




 电机槽内线圈产生的电磁力是作用在槽内的导体上还是铁芯上?
电机槽内线圈产生的电磁力是作用在槽内的导体上还是铁芯上?












评论