0x1. OpenAI Triton介绍阅读
这里来看官方的介绍:https://openai.com/research/triton ,从官方的介绍中我们可以看到OpenAI Triton的产生动机以及它的目标是什么,还可以看到一些经典算法的实现例子展示。
这里的标题是 Introducing Triton: Open-source GPU programming for neural networks ,翻译就是《介绍 Triton:用于神经网络的开源 GPU 编程语言》。然后下面的一句话翻译过来是:我们发布了 Triton 1.0,这是一种开源的类 Python 编程语言,它使得没有 CUDA 经验的研究人员能够编写高效的 GPU 代码——大多数情况下,其效能与专家所能编写的代码相当。这里指出了triton的目的,就是让编写cuda kernrl变得更简单。接下来就逐步看一下介绍里的具体内容,为了更加准确这里会截图对应的原文然后放上我的翻译或者理解。

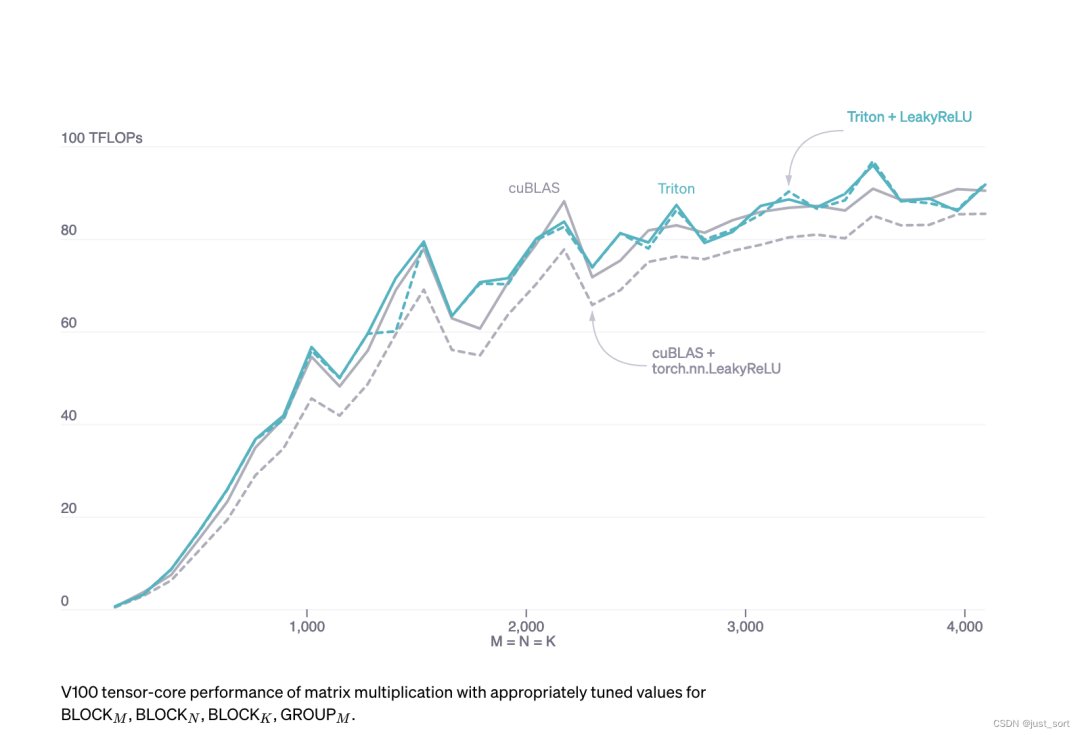
这里的意思是Triton可以使得用户用较少的努力就写出一个达到硬件峰值性能的kernel,比如使用 Triton 可以编写 FP16 矩阵乘法的核函数,其性能能够匹配 cuBLAS,并且这个代码不超过25行。然后研究者已经用Triton开发了一些高效的实现,和功能相同的Torch实现相比,性能可以达到两倍提升。后面一段就是强调了使用CUDA来把一些原始的PyTorch实现写一个算子一般会更加高效,但是这个难度不小,并且目前已有工作也不能很好覆盖这种情况,所以OpenAI Triton诞生。

这里讲的是GPU编程的挑战,现代 GPU 的架构大致可以分为三个主要部分——DRAM、SRAM 和 ALU。在优化 CUDA 代码时,必须考虑到这些组件:
从 DRAM 的内存传输必须合并成大型事务,以利用现代内存接口的大总线宽度(内存合并访问)。
数据必须在重复使用前手动存储到 SRAM 中,并进行管理来最小化bank conflict。
计算必须仔细地进行划分和调度,不仅是在流式多处理器(SMs)之间,还包括在其内部,以促进指令/线程级并行性,并利用专用的 ALU(例如,Tensor Cores)。


考虑所有这些因素可能对于拥有多年经验的资深 CUDA 程序员来说都是一个挑战。Triton 的目的是完全自动化这些优化,以便开发者能够更好地专注于他们并行代码的高层逻辑。Triton 旨在广泛适用,因此不会自动在流式多处理器(SMs)之间调度工作——留下一些重要的算法考虑(例如,tiling,跨 SM 同步)由开发者自行决定。
然后给了一个表格展示cuda的编译器和triton的区别。
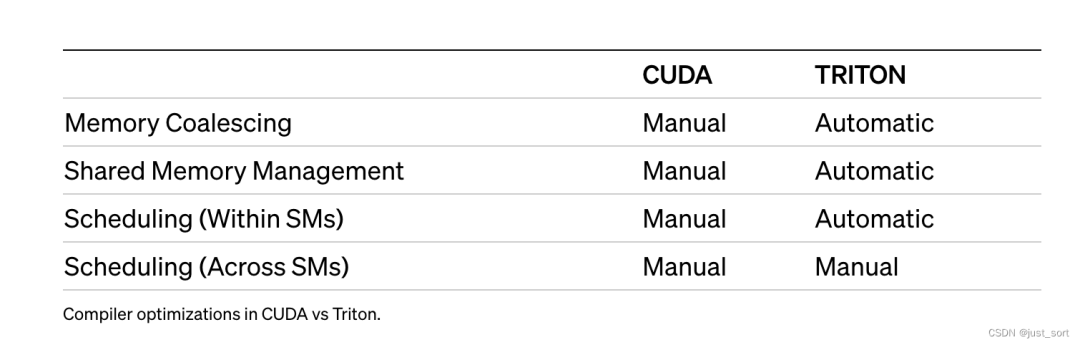

在所有可用的领域特定语言和即时编译器中,Triton可能和Numba最相似:kernel被定义为一个装饰过的函数,并以不同的 program_id 并行启动在所谓的网格实例上。然而,正如下面的代码片段所示,相似之处仅此而已:Triton 通过对块上的操作来暴露实例内部的并行性——这些小数组的尺寸是二的幂次方——而不是单指令多线程(SIMT)执行模型。这样做,Triton 有效地抽象出了所有与 CUDA 线程块内部并发相关的问题(例如,内存合并、共享内存同步/冲突、Tensor Cores调度)。
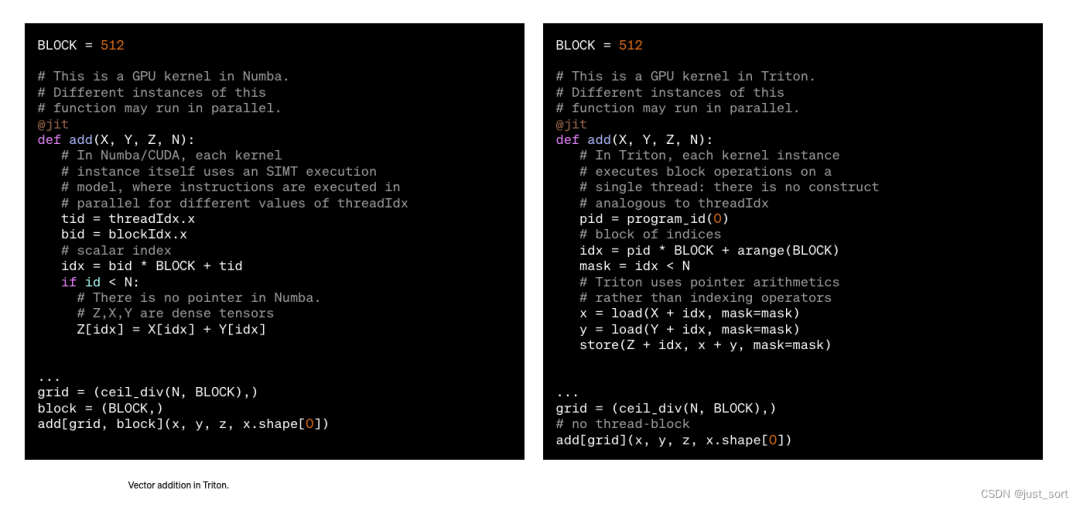


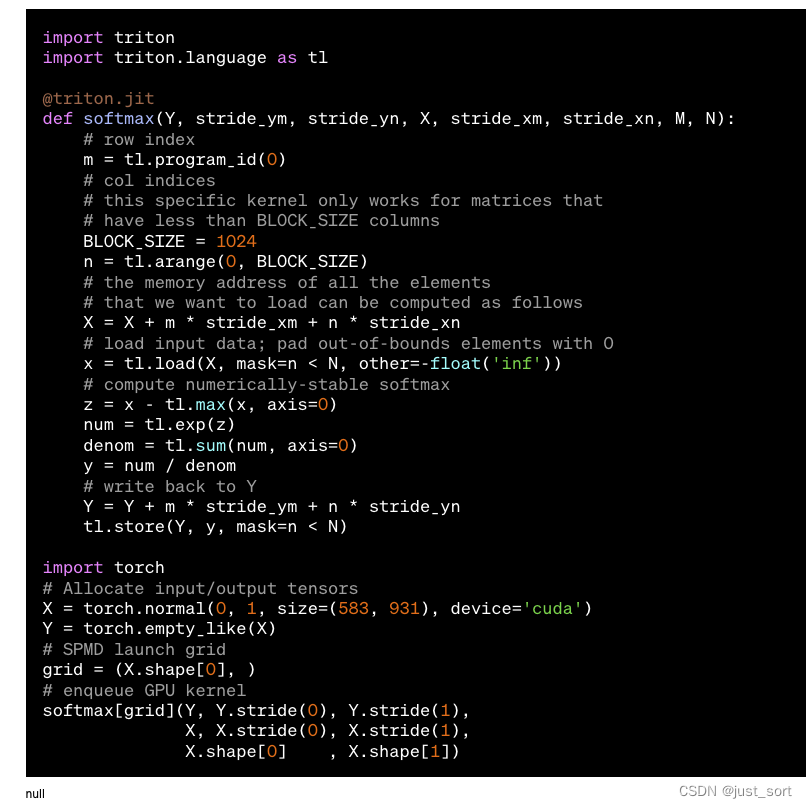
注意,Triton 的即时编译器将 X 和 Y 视为指针而不是张量;我们认为保留对内存访问的低级控制对于处理更复杂的数据结构(例如,块稀疏张量)是重要的。重要的是,这种特定的 softmax 实现在整个标准化过程中将 X 的行保留在 SRAM 中,这在适用时最大化了数据重用(约 <32K 列)。这与 PyTorch 的内部 CUDA 代码不同,后者使用临时内存使其更具通用性,但显著更慢(如下所示)。这里的关键不是 Triton 本质上更好,而是它简化了专用kernel的开发,这些内核可能比在通用库中找到的内核快得多。
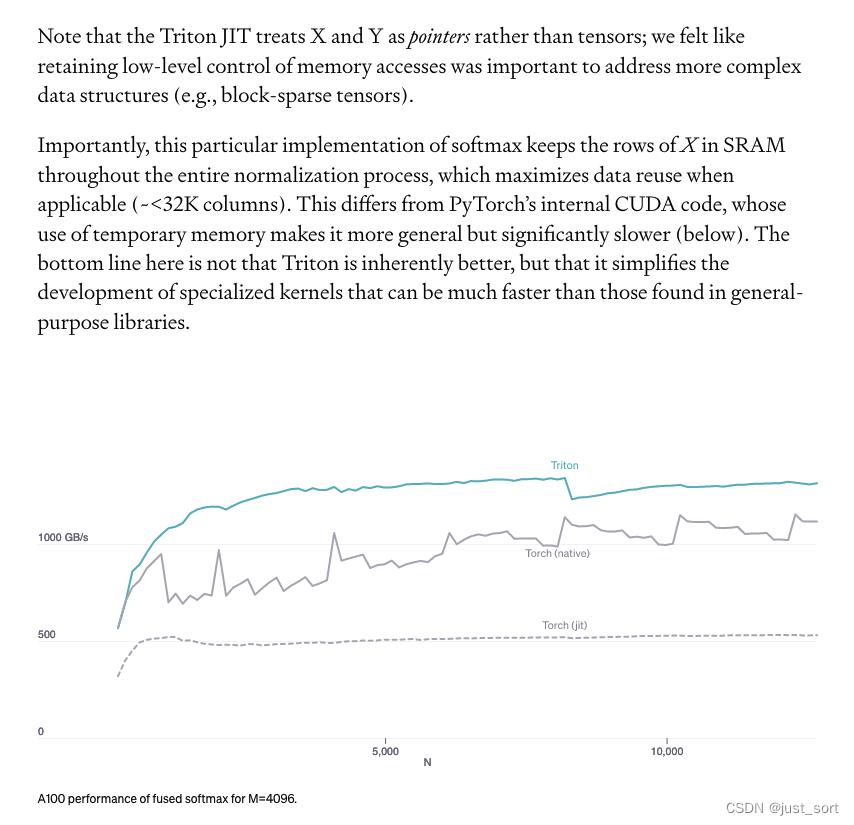
Torch(v1.9)JIT编译器的较低性能凸显了从高级张量操作序列自动生成 CUDA 代码的难度。


这里是说Triton大概只需要25行Python代码就可以实现一个接近峰值的矩阵乘法。(后面有专门的一大节讲这个代码的原理)代码如下:
@triton.jit defmatmul(A,B,C,M,N,K,stride_am,stride_ak, stride_bk,stride_bn,stride_cm,stride_cn, **META): #extractmetaparameters BLOCK_M,GROUP_M=META['BLOCK_M'],META['GROUP_M'] BLOCK_N=META['BLOCK_N'] BLOCK_K=META['BLOCK_K'] #programsaregroupedtogethertoimproveL2hitrate _pid_m=tl.program_id(0) _pid_n=tl.program_id(1) pid_m=_pid_m//GROUP_M pid_n=(_pid_n*GROUP_M)+(_pid_m%GROUP_M) #rm(resp.rn)denotesarangeofindices #forrows(resp.col)ofC rm=pid_m*BLOCK_M+tl.arange(0,BLOCK_M) rn=pid_n*BLOCK_N+tl.arange(0,BLOCK_N) #rkdenotesarangeofindicesforcolumns #(resp.rows)ofA(resp.B) rk=tl.arange(0,BLOCK_K) #thememoryaddressesofelementsinthefirstblockof #AandBcanbecomputedusingnumpy-stylebroadcasting A=A+(rm[:,None]*stride_am+rk[None,:]*stride_ak) B=B+(rk[:,None]*stride_bk+rn[None,:]*stride_bn) #initializeanditerativelyupdateaccumulator acc=tl.zeros((BLOCK_M,BLOCK_N),dtype=tl.float32) forkinrange(K,0,-BLOCK_K): a=tl.load(A) b=tl.load(B) #blocklevelmatrixmultiplication acc+=tl.dot(a,b) #incrementpointerssothatthenextblocksofAandB #areloadedduringthenextiteration A+=BLOCK_K*stride_ak B+=BLOCK_K*stride_bk #fuseleakyReLUifdesired #acc=tl.where(acc>=0,acc,alpha*acc) #writebackresult C=C+(rm[:,None]*stride_cm+rn[None,:]*stride_cn) mask=(rm[:,None]< M) & (rn[None, :] < N) tl.store(C, acc, mask=mask)
手写矩阵乘法kernel的一个重要优势是,它们可以根据需要定制,以适应输入(例如,切片)和输出(例如,LeakyReLU)的融合转换。如果没有像 Triton 这样的系统,没有出色的 GPU 编程专长的开发者将无法进行矩阵乘法内核的定制修改。
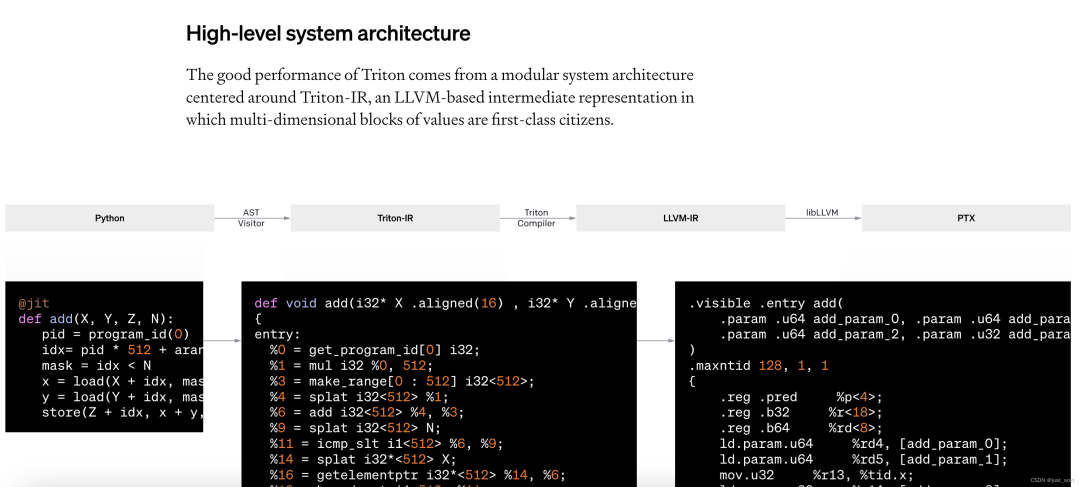
这里是说Triton 的良好性能源于一个以 Triton-IR 为中心的模块化系统架构,Triton-IR 是一个基于 LLVM 的中间表示,在这个系统中,多维值块(这个是MLIR的概念)是一等公民。GPT
@triton.jit 装饰器的工作原理是遍历提供的 Python 函数的抽象语法树(AST),以便使用常见的 SSA 构建算法即时生成 Triton-IR。然后,编译器后端会简化、优化并自动并行化所产生的 IR 代码,再将其转换为高质量的 LLVM-IR —— 最终生成 PTX —— 以在近期的 NVIDIA GPU 上执行。目前不支持 CPU 和 AMD GPU,但我们欢迎社区贡献,旨在解决这一限制。
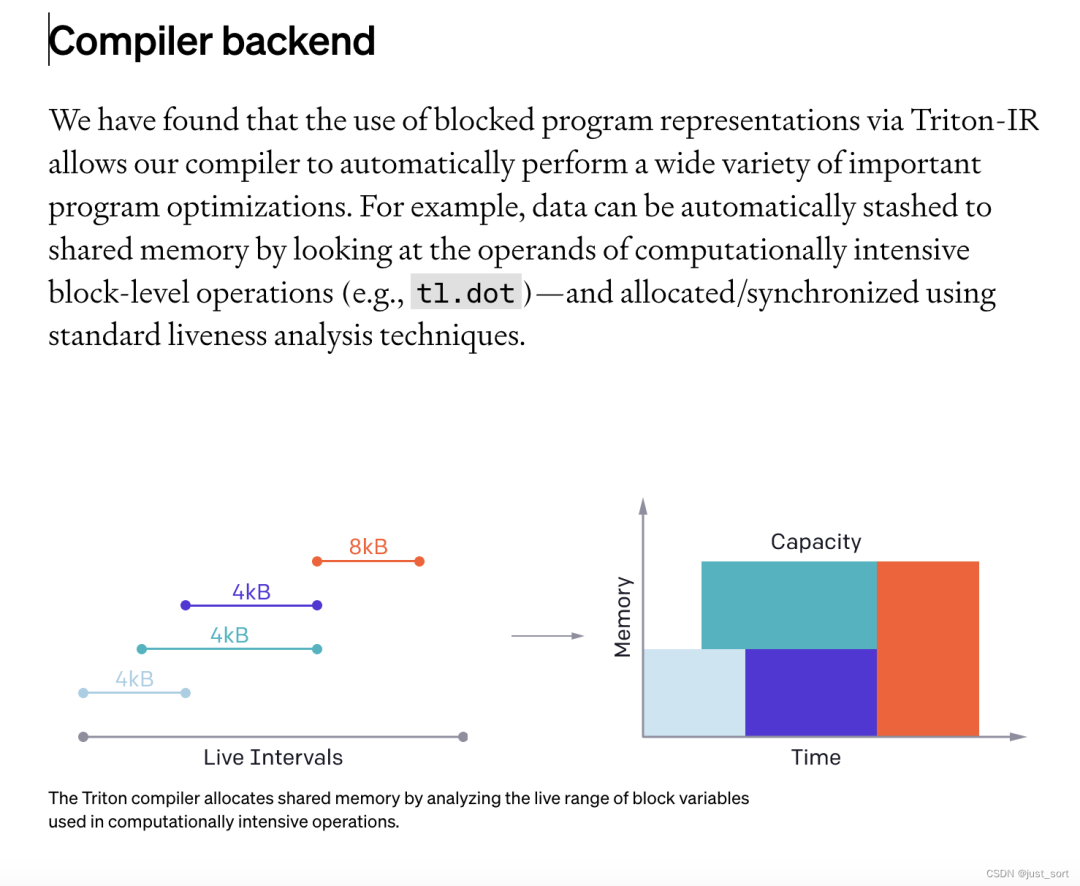
我们发现,通过 Triton-IR 使用块级别程序表示,使我们的编译器能够自动执行各种重要的程序优化。例如,可以通过观察计算密集型块级操作(例如,tl.dot)的操作数,自动将数据暂存到共享内存中,并使用标准的活性分析威廉希尔官方网站
进行分配和同步。
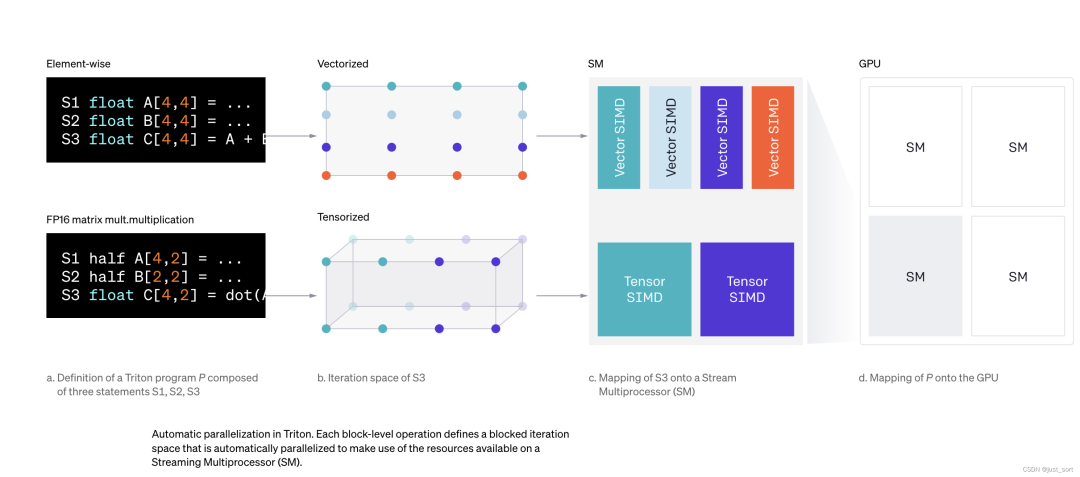
另一方面,如下所示,Triton 程序可以高效且自动地并行化,既可以(1)通过并发执行不同的kernel实例在流式多处理器(SMs)间并行,也可以(2)通过分析每个块级操作的迭代空间,并在不同的 SIMD 单元间适当分配,从而在 SMs 内部并行。
0x2. 教程1 Vector Addition阅读

意思是这一节教程会介绍Triton编程模型定义kernel的基本写法,此外也会介绍一下怎么实现一个良好的benchmark测试。下面来看计算kernel实现,我把注释改成中文了:
importtorch importtriton importtriton.languageastl @triton.jit defadd_kernel(x_ptr,#*指针*,指向第一个输入向量。 y_ptr,#*指针*,指向第二个输入向量。 output_ptr,#*指针*,指向输出向量。 n_elements,#向量的大小。 BLOCK_SIZE:tl.constexpr,#每个程序应处理的元素数量。 #注意:`constexpr`这样可以被用作形状值。 ): #这里有多个“程序”处理不同的数据。我们在这里识别我们是哪一个程序: pid=tl.program_id(axis=0)#我们使用一维启动网格,所以轴是0。 #该程序将处理从初始数据偏移的输入。 #例如,如果你有一个长度为256的向量和块大小为64,那么程序 #将分别访问元素[0:64,64:128,128:192,192:256]。 #注意偏移量是一个指针列表: block_start=pid*BLOCK_SIZE offsets=block_start+tl.arange(0,BLOCK_SIZE) #创建一个掩码以防止内存操作越界访问。 mask=offsets< n_elements # 从DRAM加载x和y,屏蔽任何额外的元素以防输入不是块大小的倍数。 x = tl.load(x_ptr + offsets, mask=mask) y = tl.load(y_ptr + offsets, mask=mask) output = x + y # 将x + y写回DRAM。 tl.store(output_ptr + offsets, output, mask=mask)
这里还声明了一个辅助函数来(1)分配z张量,(2)使用适当的网格/块大小排队上面的kernel:
defadd(x:torch.Tensor,y:torch.Tensor): #我们需要预分配输出。 output=torch.empty_like(x) assertx.is_cudaandy.is_cudaandoutput.is_cuda n_elements=output.numel() #SPMD启动网格表示并行运行的kernel实例的数量。 #它类似于CUDA启动网格。它可以是Tuple[int],也可以是Callable(metaparameters)->Tuple[int]。 #在这种情况下,我们使用一个1D网格,其大小是块的数量: grid=lambdameta:(triton.cdiv(n_elements,meta['BLOCK_SIZE']),) #注意: #-每个torch.tensor对象都隐式地转换为指向其第一个元素的指针。 #-使用`triton.jit`装饰的函数可以用一个启动网格索引来获得可调用的GPU内核。 #-不要忘记将元参数作为关键字参数传递。 add_kernel[grid](x,y,output,n_elements,BLOCK_SIZE=1024) #我们返回一个指向z的句柄,但是因为`torch.cuda.synchronize()`还没有被调用,所以这时kernel仍然 #在异步运行。 returnoutput
我们现在可以使用上面定义的函数来计算两个torch.tensor对象的逐元素求和,并测试其正确性:
torch.manual_seed(0) size=98432 x=torch.rand(size,device='cuda') y=torch.rand(size,device='cuda') output_torch=x+y output_triton=add(x,y) print(output_torch) print(output_triton) print(f'Themaximumdifferencebetweentorchandtritonis' f'{torch.max(torch.abs(output_torch-output_triton))}')
输出:
tensor([1.3713,1.3076,0.4940,...,0.6724,1.2141,0.9733],device='cuda:0') tensor([1.3713,1.3076,0.4940,...,0.6724,1.2141,0.9733],device='cuda:0') Themaximumdifferencebetweentorchandtritonis0.0

我们可以对不同大小的向量进行自定义操作的性能基准测试,以了解它相对于PyTorch的表现如何。为了简化操作,Triton提供了一系列内置工具,使我们能够简洁地绘制出自定义操作在不同问题规模下的性能图表。
@triton.testing.perf_report( triton.testing.Benchmark( x_names=['size'],#用作绘图x轴的参数名。 x_vals=[2**iforiinrange(12,28,1)],#`x_name`的不同可能值。 x_log=True,#x轴是对数的。 line_arg='provider',#其值对应于图中不同线条的参数名。 line_vals=['triton','torch'],#`line_arg`的可能值。 line_names=['Triton','Torch'],#线条的标签名称。 styles=[('blue','-'),('green','-')],#线条样式。 ylabel='GB/s',#y轴的标签名称。 plot_name='vector-add-performance',#绘图的名称。也用作保存绘图的文件名。 args={},#不在`x_names`和`y_name`中的函数参数的值。 )) defbenchmark(size,provider): x=torch.rand(size,device='cuda',dtype=torch.float32) y=torch.rand(size,device='cuda',dtype=torch.float32) quantiles=[0.5,0.2,0.8] ifprovider=='torch': ms,min_ms,max_ms=triton.testing.do_bench(lambda:x+y,quantiles=quantiles) ifprovider=='triton': ms,min_ms,max_ms=triton.testing.do_bench(lambda:add(x,y),quantiles=quantiles) gbps=lambdams:12*size/ms*1e-6 returngbps(ms),gbps(max_ms),gbps(min_ms)
gbps = lambda ms: 12 * size / ms * 1e-6这里的12表示的是数据读写的bit,因为有x和y以及z的存在,所以是3*4=12bit。现在可以运行上面的装饰函数了。传递 print_data=True 参数来查看性能数据,传递 show_plots=True 参数来绘制图表,和/或传递 save_path='/path/to/results/' 参数来将它们连同原始CSV数据一起保存到磁盘上:
benchmark.run(print_data=True,show_plots=True)
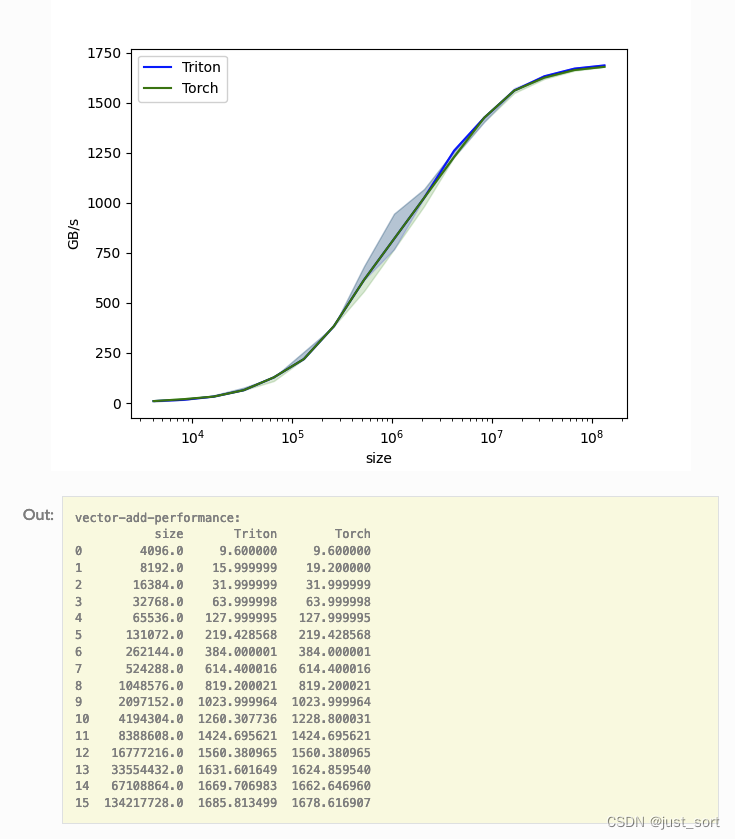
可以看到,对于elementwise任务,Triton的性能几乎和PyTorch持平,但是Triton写起来很简单。
0x3. 教程2 Fused Softmax阅读
在这个教程中,我们将编写一个融合的softmax操作,这个操作对于特定类型的矩阵来说比PyTorch的原生操作要快得多:那些行的大小可以放入GPU的SRAM中的矩阵。
通过这样做,我们将学习到:
kernel融合对于带宽受限操作的好处。
Triton中的reduce操作符。
动机
自定义GPU kernel用于逐元素加法在教育上是有价值的,但在实际应用中可能作用有限。让我们考虑一个简单的(数值稳定的)softmax操作的情况:
importtorch importtriton importtriton.languageastl @torch.jit.script defnaive_softmax(x): """使用原生pytorch计算X的逐行softmax 我们减去最大元素是为了避免溢出。Softmax对这种偏移是不变的。 """ #读取MN个元素;写入M个元素 x_max=x.max(dim=1)[0] #读取MN+M个元素;写入MN个元素 z=x-x_max[:,None] #读取MN个元素;写入MN个元素 numerator=torch.exp(z) #读取MN个元素;写入M个元素 denominator=numerator.sum(dim=1) #读取MN+M个元素;写入MN个元素 ret=numerator/denominator[:,None] #总计:读取5MN+2M个元素;写入3MN+2M个元素 returnret


计算kernel
我们的softmax kernel的工作方式如下:每个程序加载输入矩阵X的一行,对其进行归一化处理,然后将结果写回到输出Y中。需要注意的是,Triton的一个重要限制是每个块必须包含2的幂次方个元素,因此如果我们想处理任何可能的输入形状,我们需要在内部对每行进行“pad”以及对内存访问操作进行保护(也就是防止越界):
@triton.jit
defsoftmax_kernel(output_ptr,input_ptr,input_row_stride,output_row_stride,n_cols,BLOCK_SIZE:tl.constexpr):
#softmax的各行是独立的,所以我们在这些行上进行并行处理
row_idx=tl.program_id(0)
#步长代表我们需要增加多少指针来前进1行
row_start_ptr=input_ptr+row_idx*input_row_stride
#块大小是大于n_cols的下一个2的幂次,因此我们可以将每一行放入单个块中
col_offsets=tl.arange(0,BLOCK_SIZE)
input_ptrs=row_start_ptr+col_offsets
#将行加载到SRAM中,使用掩码因为BLOCK_SIZE可能大于n_cols
row=tl.load(input_ptrs,mask=col_offsets< n_cols, other=-float('inf'))
# 减去最大值以实现数值稳定性
row_minus_max = row - tl.max(row, axis=0)
# 注意在Triton中指数运算快但是近似的(即,类似于CUDA中的__expf)
numerator = tl.exp(row_minus_max)
denominator = tl.sum(numerator, axis=0)
softmax_output = numerator / denominator
# 将输出写回DRAM
output_row_start_ptr = output_ptr + row_idx * output_row_stride
output_ptrs = output_row_start_ptr + col_offsets
tl.store(output_ptrs, softmax_output, mask=col_offsets < n_cols)
解析来创建一个辅助函数,该函数为任何给定的输入张量排队执行kernel并且设置了启动参数。
defsoftmax(x): n_rows,n_cols=x.shape #块大小是大于`x`中列数的最小2的幂 BLOCK_SIZE=triton.next_power_of_2(n_cols) #我们可以使用的另一个技巧是要求编译器通过增加每行分布的warp数(`num_warps`)来使用更多的线程。 #在下一个教程中,你将看到如何以更自然的方式自动调整这个值,这样你就不必自己想出手动启发式方法。 num_warps=4 ifBLOCK_SIZE>=2048: num_warps=8 ifBLOCK_SIZE>=4096: num_warps=16 #分配输出 y=torch.empty_like(x) #排队执行内核。一维启动网格很简单:我们有每行一个内核实例 #输入矩阵 softmax_kernel[(n_rows,)]( y, x, x.stride(0), y.stride(0), n_cols, num_warps=num_warps, BLOCK_SIZE=BLOCK_SIZE, ) returny

这里是验证Triton实现的fuse softmax和PyTorch的naive实现等价,显然他们是等价的。
BenchMark

这里设定矩阵的行数为固定的4096来做benchmark。
@triton.testing.perf_report(
triton.testing.Benchmark(
x_names=['N'],#用作绘图x轴的参数名
x_vals=[128*iforiinrange(2,100)],#`x_name`的不同可能值
line_arg='provider',#其值对应于图中不同线条的参数名
line_vals=[
'triton',
'torch-native',
'torch-jit',
],#`line_arg`的可能值
line_names=[
"Triton",
"Torch(原生)",
"Torch(jit)",
],#线条的标签名称
styles=[('blue','-'),('green','-'),('green','--')],#线条样式
ylabel="GB/s",#y轴的标签名称
plot_name="softmax-performance",#绘图的名称。也用作保存绘图的文件名。
args={'M':4096},#不在`x_names`和`y_name`中的函数参数的值
))
defbenchmark(M,N,provider):
x=torch.randn(M,N,device='cuda',dtype=torch.float32)
quantiles=[0.5,0.2,0.8]
ifprovider=='torch-native':
ms,min_ms,max_ms=triton.testing.do_bench(lambda:torch.softmax(x,axis=-1),quantiles=quantiles)
ifprovider=='triton':
ms,min_ms,max_ms=triton.testing.do_bench(lambda:softmax(x),quantiles=quantiles)
ifprovider=='torch-jit':
ms,min_ms,max_ms=triton.testing.do_bench(lambda:naive_softmax(x),quantiles=quantiles)
gbps=lambdams:2*x.nelement()*x.element_size()*1e-9/(ms*1e-3)
returngbps(ms),gbps(max_ms),gbps(min_ms)
benchmark.run(show_plots=True,print_data=True)
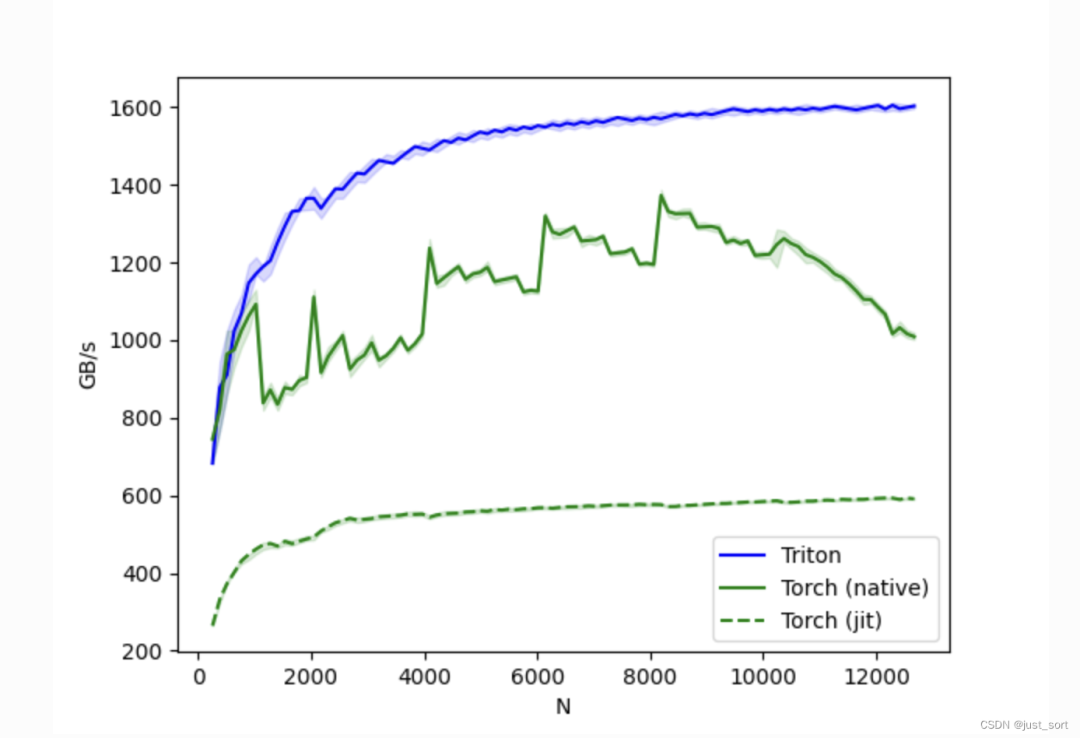
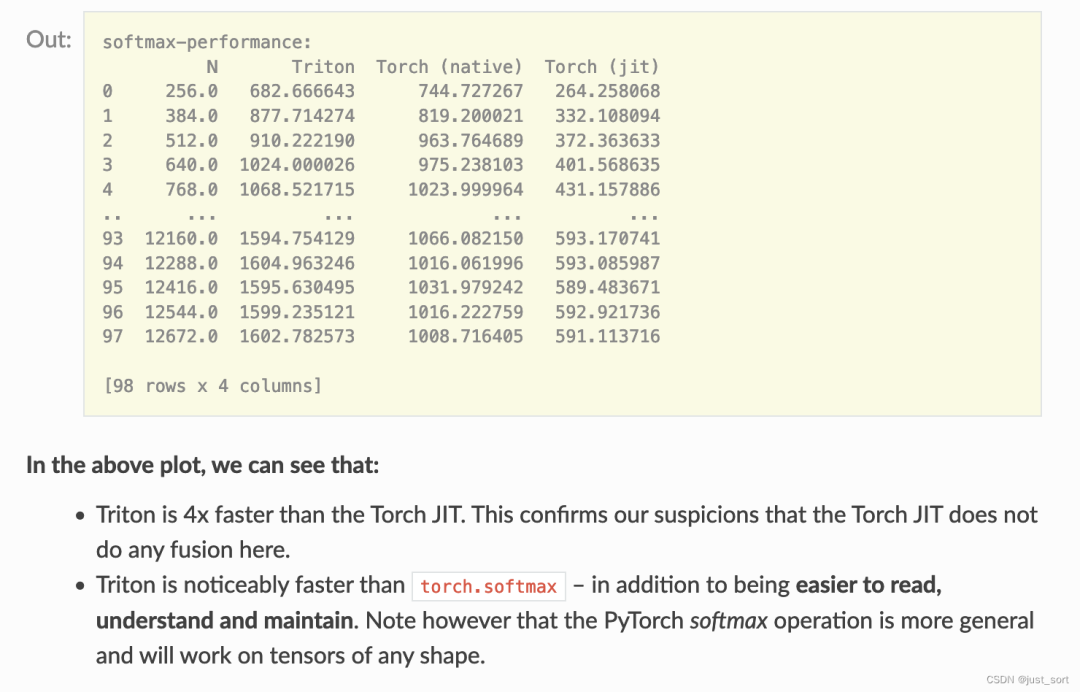
这里提到虽然Triton实现的softmax性能更好并且易于理解和维护,但PyTorch的torch.softmax则更加通用。
0x4. 教程3 Matrix Multiply阅读

首先教程指出这里就是要写一个Block级别的矩阵乘法,然后这里会涉及到多维度的指针操作,程序重排以更好的命中l2 cache以及自动调优。
动机
矩阵乘法是大多数现代高性能计算系统的关键构建块。它们众所周知难以优化,因此它们的实现通常由硬件供应商自己作为所谓的“内核库”(例如,cuBLAS)的一部分来完成。不幸的是,这些库通常是专有的,无法轻易地定制以适应现代深度学习工作负载的需求(例如,融合激活函数)。在这个教程中,你将学习如何使用Triton自己实现高效的矩阵乘法,这种方法易于定制和扩展。
大致来说,我们将要编写的内核将实现以下块级算法来乘以一个 (M, K) 矩阵和一个 (K, N) 矩阵:
#Doinparallel forminrange(0,M,BLOCK_SIZE_M): #Doinparallel forninrange(0,N,BLOCK_SIZE_N): acc=zeros((BLOCK_SIZE_M,BLOCK_SIZE_N),dtype=float32) forkinrange(0,K,BLOCK_SIZE_K): a=A[m:m+BLOCK_SIZE_M,k:k+BLOCK_SIZE_K] b=B[k:k+BLOCK_SIZE_K,n:n+BLOCK_SIZE_N] acc+=dot(a,b) C[m:m+BLOCK_SIZE_M,n:n+BLOCK_SIZE_N]=acc
其中,双重嵌套的for循环的每次迭代都由一个专用的Triton program实例执行。
计算kernel
上述算法实际上在Triton中相当容易实现。主要的难点来自于在内循环中计算必须读取A和B块的内存位置。为此,我们需要多维指针运算。
指针运算
对于一个2D Tensor X,X[i, j]的内存位置为&X[i, j] = X + i*stride_xi + j*stride_xj。因此,对于A[m : m+BLOCK_SIZE_M, k:k+BLOCK_SIZE_K]和B[k : k+BLOCK_SIZE_K, n : n+BLOCK_SIZE_N]的块指针可以用下面的伪代码定义:
&A[m:m+BLOCK_SIZE_M,k:k+BLOCK_SIZE_K]=a_ptr+(m:m+BLOCK_SIZE_M)[:,None]*A.stride(0)+(k:k+BLOCK_SIZE_K)[None,:]*A.stride(1); &B[k:k+BLOCK_SIZE_K,n:n+BLOCK_SIZE_N]=b_ptr+(k:k+BLOCK_SIZE_K)[:,None]*B.stride(0)+(n:n+BLOCK_SIZE_N)[None,:]*B.stride(1);
这意味着A和B块的指针可以在Triton中初始化,比如 k=0 如下代码所示。另外注意,我们需要一个额外的模运算来处理M不是BLOCK_SIZE_M的倍数或N不是BLOCK_SIZE_N的倍数的情况,在这种情况下,我们可以用一些无用的值填充数据,这些值不会对结果产生影响。对于K维度,我们稍后将使用掩码加载语义来处理。
offs_am=(pid_m*BLOCK_SIZE_M+tl.arange(0,BLOCK_SIZE_M))%M offs_bn=(pid_n*BLOCK_SIZE_N+tl.arange(0,BLOCK_SIZE_N))%N offs_k=tl.arange(0,BLOCK_SIZE_K) a_ptrs=a_ptr+(offs_am[:,None]*stride_am+offs_k[None,:]*stride_ak) b_ptrs=b_ptr+(offs_k[:,None]*stride_bk+offs_bn[None,:]*stride_bn)
然后在内循环中按如下方式更新:
a_ptrs+=BLOCK_SIZE_K*stride_ak; b_ptrs+=BLOCK_SIZE_K*stride_bk;
如上所述,每个program实例计算一个 [BLOCK_SIZE_M, BLOCK_SIZE_N] 大小的C矩阵块。重要的是要记住,这些块的计算顺序是很重要的,因为它会影响我们程序的L2缓存命中率,不幸的是,一个简单的行优先顺序是不够的。
pid=triton.program_id(0); grid_m=(M+BLOCK_SIZE_M-1)//BLOCK_SIZE_M; grid_n=(N+BLOCK_SIZE_N-1)//BLOCK_SIZE_N; pid_m=pid/grid_n; pid_n=pid%grid_n;
L2 Cache优化
如上所述,每个程序实例计算一个 [BLOCK_SIZE_M, BLOCK_SIZE_N] 大小的C矩阵块。重要的是要记住,这些块的计算顺序很重要,因为它会影响我们程序的L2缓存命中率,不幸的是,一个简单的行主序排序是不够的。
一个可能的解决方案是以一种促进数据重用的顺序启动块。这可以通过在切换到下一列之前将块在GROUP_M行的super group中分组来实现:
#程序ID pid=tl.program_id(axis=0) #沿M轴的程序ID数量 num_pid_m=tl.cdiv(M,BLOCK_SIZE_M) #沿N轴的程序ID数量 num_pid_n=tl.cdiv(N,BLOCK_SIZE_N) #组中的程序数量 num_pid_in_group=GROUP_SIZE_M*num_pid_n #该程序所在组的ID group_id=pid//num_pid_in_group #组中第一个程序的行ID first_pid_m=group_id*GROUP_SIZE_M #如果`num_pid_m`不能被`GROUP_SIZE_M`整除,最后一个组更小 group_size_m=min(num_pid_m-first_pid_m,GROUP_SIZE_M) #*在组内*,程序按列主序排列 #程序在*启动网格*中的行ID pid_m=first_pid_m+(pid%group_size_m) #程序在*启动网格*中的列ID pid_n=(pid%num_pid_in_group)//group_size_m
例如,在下面的矩阵乘法中,每个矩阵由9个块乘以9个块组成,我们可以看到,如果我们按行主序计算输出,我们需要将90个块加载到SRAM中以计算前9个输出块,但如果我们按grouped ordering进行计算,我们只需要加载54个块。
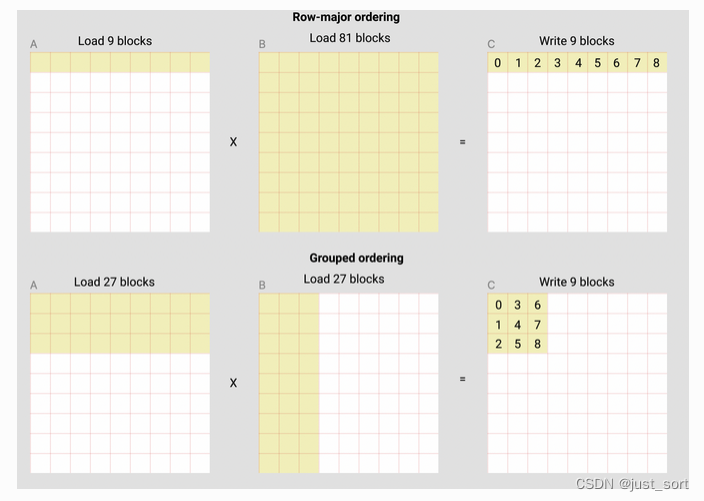
在实际应用中,这可以在某些硬件架构上提高我们矩阵乘法内核的性能超过10%(例如,在A100上从220提升到245 TFLOPS)。
L2 Cache优化原理补充讲解
上面的group oredering的访问代码比较难理解,这里来更详细的解析一下。

#程序ID pid=tl.program_id(axis=0) #沿M轴的程序ID数量 num_pid_m=tl.cdiv(M,BLOCK_SIZE_M) #沿N轴的程序ID数量 num_pid_n=tl.cdiv(N,BLOCK_SIZE_N)
这里的num_pid_m和num_pid_n就是求分别要在M和N方向循环多少次。
然后上面图中的黑色数字其实就可以理解为program id,我们可以看到program id增加的方向其实就代表了遍历的ordering,对于row major来说就是在行方向上顺序遍历,而对于group ordering来说就是按照一个BLOCK_SIZE_M*BLOCK_SIZE_N这么大的一个小组来遍历。其实这段代码就是完成group ordering的遍历:
num_pid_in_group=GROUP_SIZE_M*num_pid_n group_id=pid//num_pid_in_group first_pid_m=group_id*GROUP_SIZE_M group_size_m=min(num_pid_m-first_pid_m,GROUP_SIZE_M) pid_m=first_pid_m+(pid%group_size_m) pid_n=(pid%num_pid_in_group)//group_size_m
以上面图来看,num_pid_m=3,num_pid_n=3,num_pid_in_group=group_id * GROUP_SIZE_M=9*3=27,也就是下面的红色框里面的program个数,从名字也可以看出来这个红色框划分的区域也是一个group。
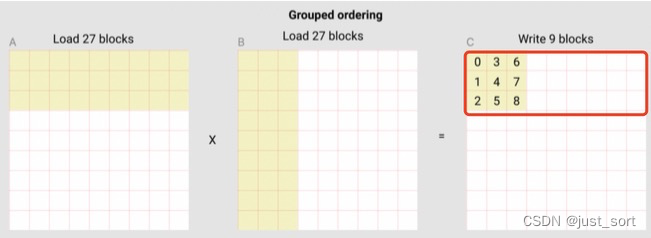
group_id 就表示当前的这次 "循环", 是在第几个红色框里,以program 0为例,这里为group_id = pid // num_pid_in_group=0//27=0。而first_pid_m 代表当前 group 中的第一个黄色program在全局的M维度上是第几个program ,这里为first_pid_m = group_id * GROUP_SIZE_M=0,group_size_m = min(num_pid_m - first_pid_m, GROUP_SIZE_M)这里是考虑到最后一个group可能占不满数据(存在padding),所以就做一个截断处理。
pid_m=first_pid_m+(pid%group_size_m) pid_n=(pid%num_pid_in_group)//group_size_m
这两行代码计算当前的program处理的黄色小块坐标([pid_m, pid_n]),pid_m这行是在行方向上移动,pid_n这行则是保证在上面的红色框里面一定是一列一列来访问的。
作为对比,在Row-major的方法中,访问方式应该是这样的:
pid_m=pid//num_pid_n pid_n=pid%num_pid_n
计算最后的结果
有了上面的铺垫,我们就可以计算最终的结果了,下面的代码展示了完整的Triton 矩阵乘法kernel实现。
#使用`triton.jit`装饰的函数可以通过`triton.autotune`装饰器进行自动调优,该装饰器包括:
#-一系列定义不同配置的`triton.Config`对象,
#这些配置涉及元参数(例如`BLOCK_SIZE_M`)和编译选项(例如`num_warps`)的不同设置
#-一个自动调优*关键字*,其值的变化将触发对所有
#提供的配置的评估
@triton.autotune(
configs=[
#每个Config定义了一组特定的配置参数和编译选项
triton.Config({'BLOCK_SIZE_M':128,'BLOCK_SIZE_N':256,'BLOCK_SIZE_K':64,'GROUP_SIZE_M':8},num_stages=3,
num_warps=8),
triton.Config({'BLOCK_SIZE_M':64,'BLOCK_SIZE_N':256,'BLOCK_SIZE_K':32,'GROUP_SIZE_M':8},num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M':128,'BLOCK_SIZE_N':128,'BLOCK_SIZE_K':32,'GROUP_SIZE_M':8},num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M':128,'BLOCK_SIZE_N':64,'BLOCK_SIZE_K':32,'GROUP_SIZE_M':8},num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M':64,'BLOCK_SIZE_N':128,'BLOCK_SIZE_K':32,'GROUP_SIZE_M':8},num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M':128,'BLOCK_SIZE_N':32,'BLOCK_SIZE_K':32,'GROUP_SIZE_M':8},num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M':64,'BLOCK_SIZE_N':32,'BLOCK_SIZE_K':32,'GROUP_SIZE_M':8},num_stages=5,
num_warps=2),
triton.Config({'BLOCK_SIZE_M':32,'BLOCK_SIZE_N':64,'BLOCK_SIZE_K':32,'GROUP_SIZE_M':8},num_stages=5,
num_warps=2),
],
key=['M','N','K'],#自动调优关键字
)
@triton.jit
defmatmul_kernel(
#指向矩阵的指针
a_ptr,b_ptr,c_ptr,
#矩阵维度
M,N,K,
#步长变量表示在特定维度上移动1个元素时指针增加的量。
#例如`stride_am`是将`a_ptr`增加多少以获取下一行的元素(A有M行)。
stride_am,stride_ak,#A矩阵的步长
stride_bk,stride_bn,#B矩阵的步长
stride_cm,stride_cn,#C矩阵的步长
#元参数
BLOCK_SIZE_M:tl.constexpr,BLOCK_SIZE_N:tl.constexpr,BLOCK_SIZE_K:tl.constexpr,#
GROUP_SIZE_M:tl.constexpr,#
ACTIVATION:tl.constexpr#激活函数
):
"""用于计算矩阵乘法C=AxB的内核。
A的形状为(M,K),B的形状为(K,N),C的形状为(M,N)。
"""
#-----------------------------------------------------------
#将程序ID`pid`映射到它应该计算的C矩阵的块。
#这是以groupedordering完成的,以促进L2数据重用。
#详细解释看一节
pid=tl.program_id(axis=0)
num_pid_m=tl.cdiv(M,BLOCK_SIZE_M)
num_pid_n=tl.cdiv(N,BLOCK_SIZE_N)
num_pid_in_group=GROUP_SIZE_M*num_pid_n
group_id=pid//num_pid_in_group
first_pid_m=group_id*GROUP_SIZE_M
group_size_m=min(num_pid_m-first_pid_m,GROUP_SIZE_M)
pid_m=first_pid_m+(pid%group_size_m)
pid_n=(pid%num_pid_in_group)//group_size_m
#----------------------------------------------------------
#为A和B的第一个块创建指针。
#我们将在K方向移动时推进这个指针并累加
#`a_ptrs`是[BLOCK_SIZE_M,BLOCK_SIZE_K]块的指针
#`b_ptrs`是[BLOCK_SIZE_K,BLOCK_SIZE_N]块的指针
#有关详细信息,请参阅上方“指针算术”部分
offs_am=(pid_m*BLOCK_SIZE_M+tl.arange(0,BLOCK_SIZE_M))%M
offs_bn=(pid_n*BLOCK_SIZE_N+tl.arange(0,BLOCK_SIZE_N))%N
offs_k=tl.arange(0,BLOCK_SIZE_K)
a_ptrs=a_ptr+(offs_am[:,None]*stride_am+offs_k[None,:]*stride_ak)
b_ptrs=b_ptr+(offs_k[:,None]*stride_bk+offs_bn[None,:]*stride_bn)
#-----------------------------------------------------------
#迭代以计算C矩阵的一个块。
#我们将累加到一个`[BLOCK_SIZE_M,BLOCK_SIZE_N]`块
#的fp32值以获得更高的精度。
#`accumulator`在循环后会转换回fp16。
accumulator=tl.zeros((BLOCK_SIZE_M,BLOCK_SIZE_N),dtype=tl.float32)
forkinrange(0,tl.cdiv(K,BLOCK_SIZE_K)):
#LoadthenextblockofAandB,generateamaskbycheckingtheKdimension.
#Ifitisoutofbounds,setitto0.
a=tl.load(a_ptrs,mask=offs_k[None,:]< K - k * BLOCK_SIZE_K, other=0.0)
b = tl.load(b_ptrs, mask=offs_k[:, None] < K - k * BLOCK_SIZE_K, other=0.0)
# We accumulate along the K dimension.
accumulator += tl.dot(a, b)
# Advance the ptrs to the next K block.
a_ptrs += BLOCK_SIZE_K * stride_ak
b_ptrs += BLOCK_SIZE_K * stride_bk
# 当累加器仍然是FP32时,可以融合任意激活函数
if ACTIVATION == "leaky_relu":
accumulator = leaky_relu(accumulator)
c = accumulator.to(tl.float16)
# -----------------------------------------------------------
# 使用掩码将输出矩阵C的块写回。
offs_cm = pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)
offs_cn = pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)
c_ptrs = c_ptr + stride_cm * offs_cm[:, None] + stride_cn * offs_cn[None, :]
c_mask = (offs_cm[:, None] < M) & (offs_cn[None, :] < N)
tl.store(c_ptrs, c, mask=c_mask)
# 我们可以通过将其作为`ACTIVATION`元参数提供给`_matmul`来融合`leaky_relu`。
@triton.jit
def leaky_relu(x):
x = x + 1
return tl.where(x >=0,x,0.01*x)
我们现在可以创建一个方便的封装函数,它只需要两个输入张量,并且会:(1)检查任何形状约束;(2)分配输出;(3)启动上述kernel。
defmatmul(a,b,activation=""): #Checkconstraints. asserta.shape[1]==b.shape[0],"Incompatibledimensions" asserta.is_contiguous(),"MatrixAmustbecontiguous" assertb.is_contiguous(),"MatrixBmustbecontiguous" M,K=a.shape K,N=b.shape #Allocatesoutput. c=torch.empty((M,N),device=a.device,dtype=a.dtype) #1Dlaunchkernelwhereeachblockgetsitsownprogram. grid=lambdaMETA:(triton.cdiv(M,META['BLOCK_SIZE_M'])*triton.cdiv(N,META['BLOCK_SIZE_N']),) matmul_kernel[grid]( a,b,c,# M,N,K,# a.stride(0),a.stride(1),# b.stride(0),b.stride(1),# c.stride(0),c.stride(1),# ACTIVATION=activation# ) returnc
计算过程的补充说明
上面的《L2 Cache优化原理补充讲解》这一节明确了kernel的group ordering的访问方式以及实现,现在来看对于当前的program实例具体是怎么计算的。现在以计算C中的第一个Block的(0, 0)为例子,它需要从A和B分别加载9个黄色的小块数据相乘并累加最后得到C中的(0, 0)位置结果。如下图所示:
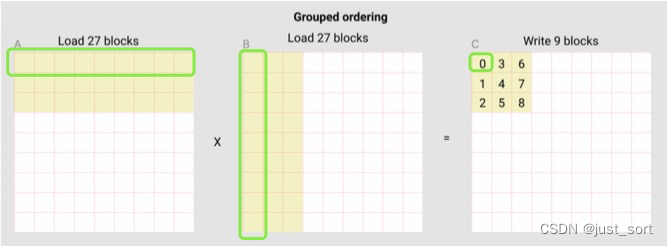
下面的代码先把program实例当前要处理A和B的第一个Block加载上来:
#---------------------------------------------------------- #为A和B的第一个块创建指针。 #我们将在K方向移动时推进这个指针并累加 #`a_ptrs`是[BLOCK_SIZE_M,BLOCK_SIZE_K]块的指针 #`b_ptrs`是[BLOCK_SIZE_K,BLOCK_SIZE_N]块的指针 #有关详细信息,请参阅上方“指针算术”部分 offs_am=(pid_m*BLOCK_SIZE_M+tl.arange(0,BLOCK_SIZE_M))%M offs_bn=(pid_n*BLOCK_SIZE_N+tl.arange(0,BLOCK_SIZE_N))%N offs_k=tl.arange(0,BLOCK_SIZE_K) a_ptrs=a_ptr+(offs_am[:,None]*stride_am+offs_k[None,:]*stride_ak) b_ptrs=b_ptr+(offs_k[:,None]*stride_bk+offs_bn[None,:]*stride_bn)
这里的a_ptr 是整个 A 矩阵第一个元素的地址,offs_am和offs_bn表示当前的program id在M维度和K维度的坐标,这个坐标是一个list,用tl.arange(0, BLOCK_SIZE_K)来获取。
得到 M 维度 和 K 维度的坐标后, 就可以让它们各自和 M 维度 和 K 维度的 stride 相乘, 然后和 a_ptr 相加, 就可以得到 A 矩阵 9 个 block 中第一个 block 中每个元素的地址了。 b_ptr也是同理。
最后一部分就是累加了,这里会在K维度上进行累加,每次计算输出的一个块。
#迭代以计算C矩阵的一个块。 #我们将累加到一个`[BLOCK_SIZE_M,BLOCK_SIZE_N]`块 #的fp32值以获得更高的精度。 #`accumulator`在循环后会转换回fp16。 accumulator=tl.zeros((BLOCK_SIZE_M,BLOCK_SIZE_N),dtype=tl.float32) forkinrange(0,tl.cdiv(K,BLOCK_SIZE_K)): #LoadthenextblockofAandB,generateamaskbycheckingtheKdimension. #Ifitisoutofbounds,setitto0. a=tl.load(a_ptrs,mask=offs_k[None,:]< K - k * BLOCK_SIZE_K, other=0.0) b = tl.load(b_ptrs, mask=offs_k[:, None] < K - k * BLOCK_SIZE_K, other=0.0) # We accumulate along the K dimension. accumulator += tl.dot(a, b) # Advance the ptrs to the next K block. a_ptrs += BLOCK_SIZE_K * stride_ak b_ptrs += BLOCK_SIZE_K * stride_bk
这行代码a = tl.load(a_ptrs, mask=offs_k[None, :] < K - k * BLOCK_SIZE_K, other=0.0)考虑到 K 可能不能被 BLOCK_SIZE_K 整除, 到每一行最后一个 block 的时候, 实际大小是不足 BLOCK_SIZE_K 的,所以需要把超出的那部分元素mask掉。
最后这部分代码是把当前的算子和LeakyReLU激活函数进行融合:
#当累加器仍然是FP32时,可以融合任意激活函数 ifACTIVATION=="leaky_relu": accumulator=leaky_relu(accumulator) c=accumulator.to(tl.float16)
单元测试
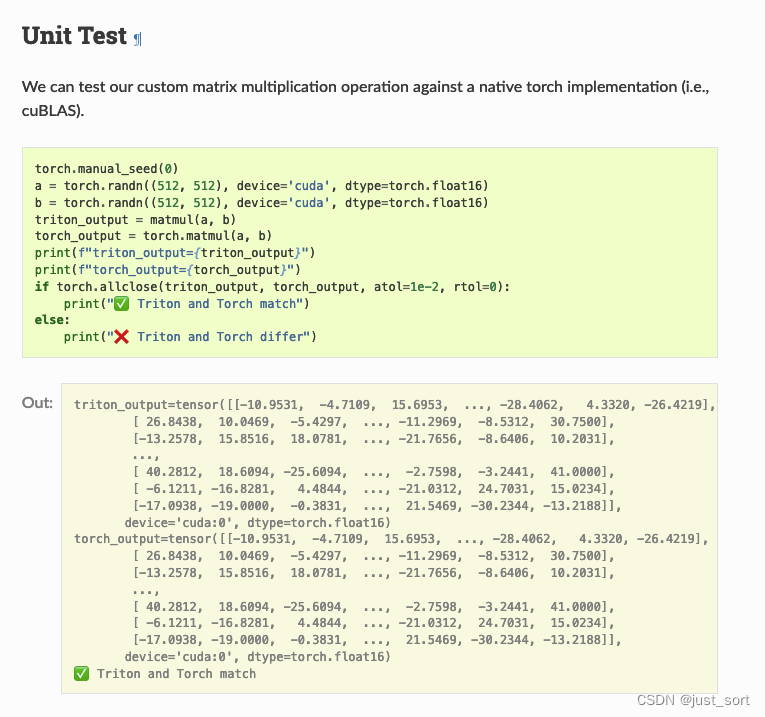
Benchmark
这里使用一个方阵来对比Triton实现的matmul kernel和cublas的matmul kernel的性能。
@triton.testing.perf_report(
triton.testing.Benchmark(
x_names=['M','N','K'],#用作图表x轴的参数名
x_vals=[128*iforiinrange(2,33)],#`x_name`的不同可能值
line_arg='provider',#其值对应于图表中不同线条的参数名
#`line_arg`的可能值
line_vals=['cublas','triton'],
#线条的标签名称
line_names=["cuBLAS","Triton"],
#线条样式
styles=[('green','-'),('blue','-')],
ylabel="TFLOPS",#y轴的标签名称
plot_name="matmul-performance",#图表的名称,也用作保存图表的文件名。
args={},#其他参数
))
defbenchmark(M,N,K,provider):
#初始化张量
a=torch.randn((M,K),device='cuda',dtype=torch.float16)
b=torch.randn((K,N),device='cuda',dtype=torch.float16)
quantiles=[0.5,0.2,0.8]#分位数
#如果提供者是cublas
ifprovider=='cublas':
ms,min_ms,max_ms=triton.testing.do_bench(lambda:torch.matmul(a,b),quantiles=quantiles)
#如果提供者是triton
ifprovider=='triton':
ms,min_ms,max_ms=triton.testing.do_bench(lambda:matmul(a,b),quantiles=quantiles)
#性能计算函数
perf=lambdams:2*M*N*K*1e-12/(ms*1e-3)
returnperf(ms),perf(max_ms),perf(min_ms)
#运行基准测试,展示图表和打印数据
benchmark.run(show_plots=True,print_data=True)
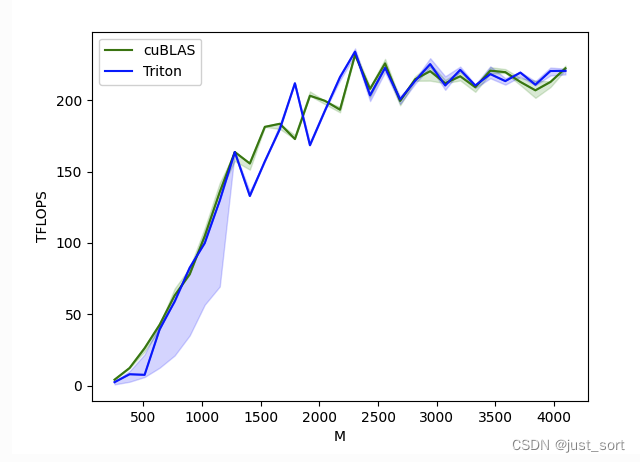
可以看到基于Triton实现的矩阵乘kernel性能大体可以和高度优化的cuBlas持平。
审核编辑:刘清
-
sram
+关注
关注
6文章
765浏览量
114654 -
多处理器
+关注
关注
0文章
22浏览量
8918 -
Cache
+关注
关注
0文章
129浏览量
28320 -
python
+关注
关注
56文章
4785浏览量
84533 -
OpenAI
+关注
关注
9文章
1062浏览量
6442
原文标题:【BBuf的CUDA笔记】十三,OpenAI Triton 入门笔记一
文章出处:【微信号:GiantPandaCV,微信公众号:GiantPandaCV】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐




 【BBuf的CUDA笔记】OpenAI Triton入门笔记一
【BBuf的CUDA笔记】OpenAI Triton入门笔记一














评论