这次的文章,我们来看一看三维空间直角坐标系的平移和旋转变换,尽管这个内容早已见诸文献资料,但自己在看书籍以及期刊论文时,总是遇到让人百思不得其解的事情,就是不同的文献给出的同类型的旋转矩阵居然有不一样的,这让小D对文献中的公式产生了怀疑,也不知道哪个旋转矩阵才是对的。
于是,自己动手,丰衣足食,为了验证公式的正确性,小D把旋转矩阵推了个遍,包括文献中只给出了公式而没有过程的旋转矩阵的推导。
三维空间直角坐标系的平移变换
文章的开头,还是先讲讲坐标系的平移变换,平移变换的过程如下图所示:
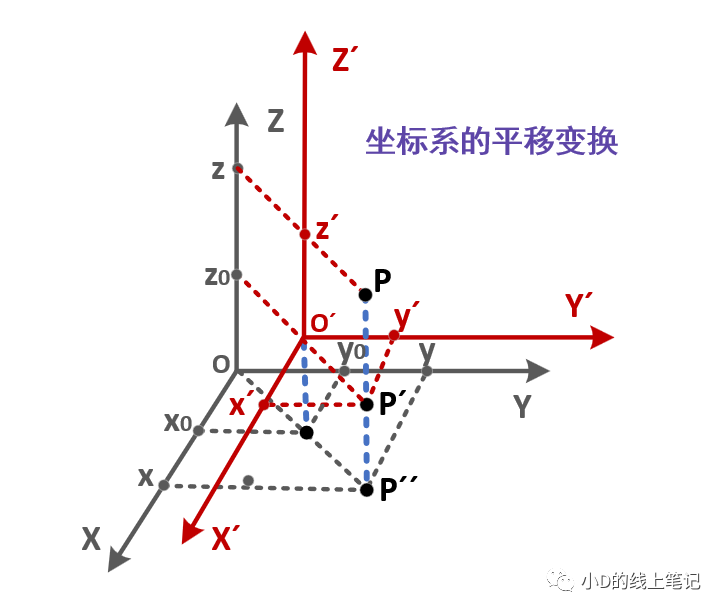
假设点P是空间中的任意一点,其在XYZ坐标系中的坐标为(x, y, z)。现在点P不动,我们将XYZ坐标系做一个平移的操作,把XYZ平移到X´Y´Z´的位置,O´是平移后的坐标的原点,要注意的是,O´在XYZ中的坐标为(x0, y0, z0)。点P在XYZ坐标系中的坐标为(x, y, z),点P在平移后的坐标系X´Y´Z´中的坐标为(x´, y´, z´)。根据上面这个示意图,聪明的你一下就可以发现:
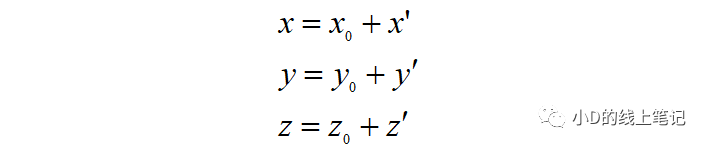
通过上面的式子,我们可以求解出点P在X´Y´Z´坐标系中的坐标为:
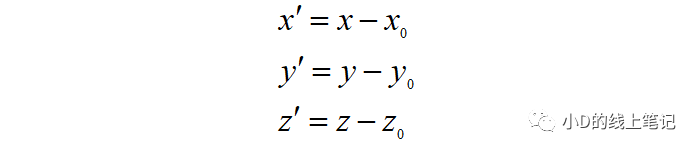
把上面的式子转换成矩阵的形式就是:
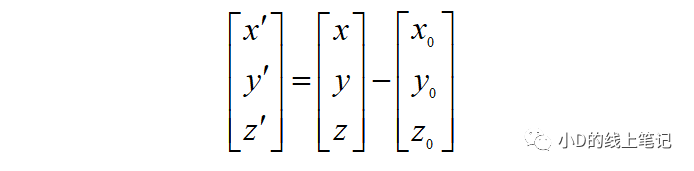
这就是三维空间直角坐标系的平移变换了。
三维空间直角坐标系的旋转变换
下面我们来看看三维空间直角坐标系的旋转变换,小D最开始在研究旋转变换的时候,只推导了右手坐标系的旋转变换。有一次看到了一篇文献,它用的是左手坐标系,但小D对文献中给出的公式的正确性感到怀疑,而我们要在代码中用到相关的坐标转换,这意味着我们需要知道左手坐标系旋转矩阵的正确表达式,所以小D又把左手坐标系的旋转矩阵推导了一遍。
右手坐标系的旋转变换
右手坐标系的旋转过程有三个,分别是绕X,Y,Z轴旋转,右手坐标系在旋转时,通常规定以逆时针旋转方向为正方向。
①XYZ右手坐标系绕X轴逆时针旋转θ角
先来推导右手坐标系绕X轴旋转的旋转矩阵,这个过程可以用下面这个示意图表示:
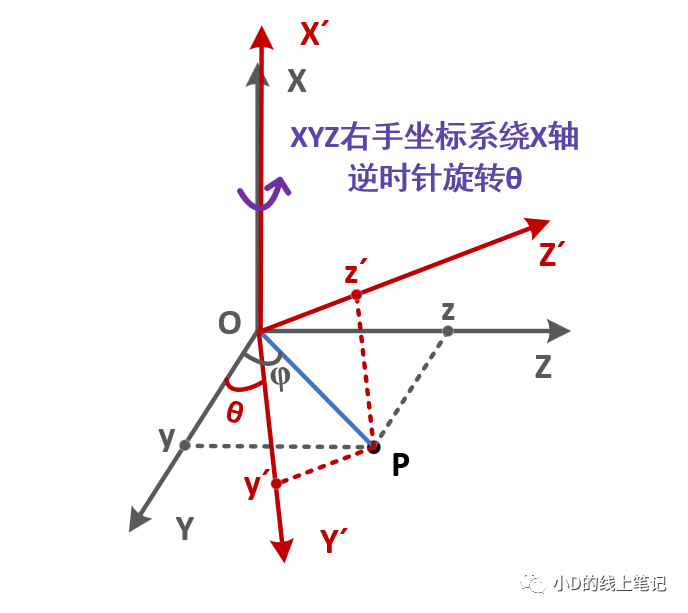
假设P点为空间中任意一点,为了便于观察与推导,我们将P点放在YOZ平面内。P点在空间中保持不动,XYZ坐标系绕X轴逆时针旋转θ形成新的坐标系X´Y´Z´,P点在XYZ中的坐标为(x, y, z),P点在X´Y´Z´中的坐标为(x´, y´, z´),现在我们已知(x, y, z)、旋转角度θ和(x´, y´, z´),求旋转矩阵Rx。在推导的过程中,我们还要假设一个变量,就是点P相对于Y轴正方向逆时针的夹角为φ。
很明显,点P在XYZ坐标系中的Y,Z轴坐标可以表示为:
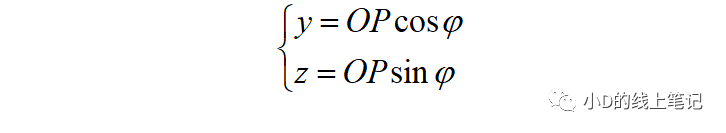
点P在X´Y´Z´坐标系中Y´,Z´轴坐标为:
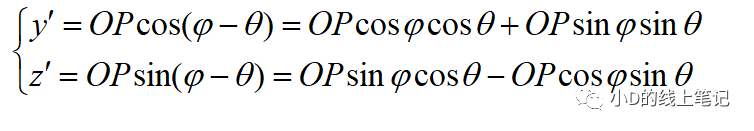
把x,y带入x´,y´中,同时P点在XYZ中X轴坐标与其在X´Y´Z´坐标系中的X´轴坐标是相等的,所以有:
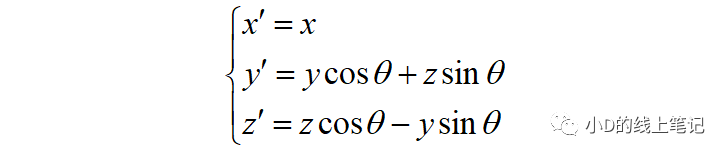
把这个表达式表示成矩阵相乘的形式为:
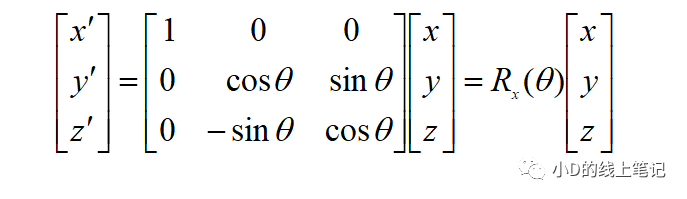
上面的Rx就是XYZ右手坐标系绕X轴逆时针旋转θ角,空间中的点从XYZ坐标系变换到X´Y´Z´坐标系的旋转矩阵,Rx的表达式为:
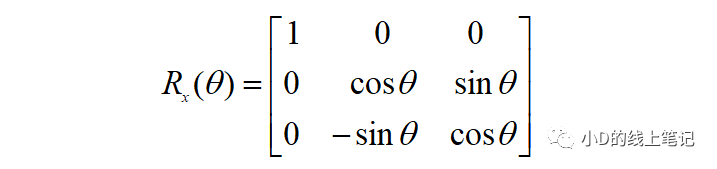
②XYZ右手坐标系绕Y轴逆时针旋转θ角
有了前面的推导过程,XYZ右手坐标系绕Y轴逆时针旋转θ角的旋转矩阵的推导就一葫芦画瓢了。旋转过程如下图所示:
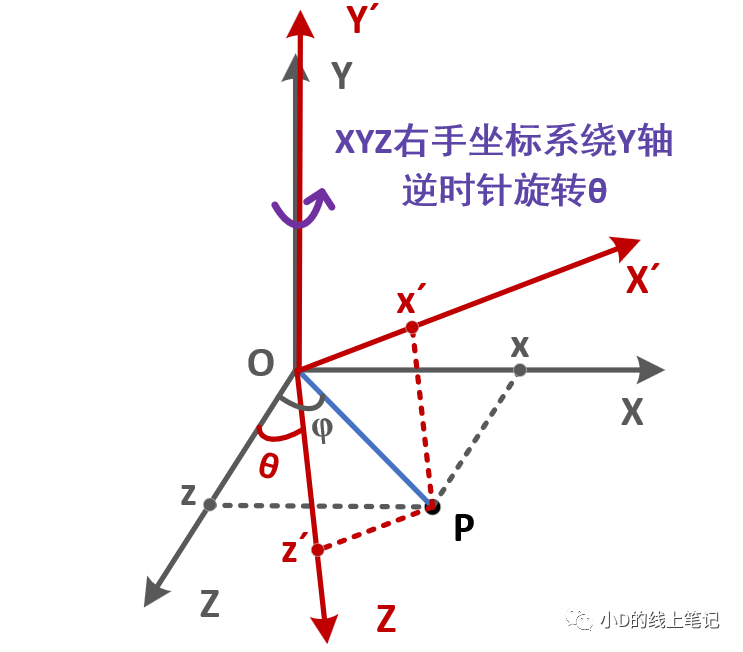
点P在XYZ右手坐标系中的X,Z轴坐标为:
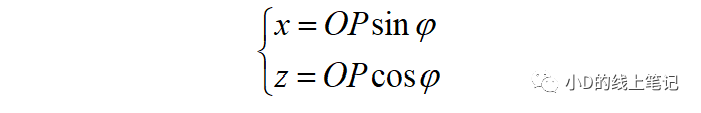
点P在X´Y´Z´坐标系中的X,Z轴坐标为:
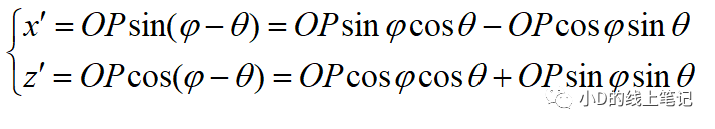
把x,z带入x´,z´中,同时P点在XYZ中的Y轴坐标与X´Y´Z´坐标系中的Y´轴坐标是相等的,所以有:
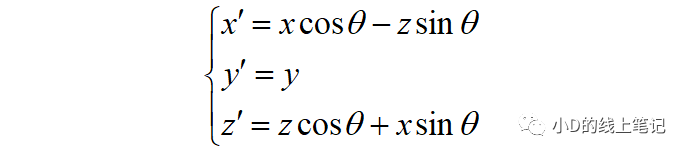
写成矩阵相乘的形式:
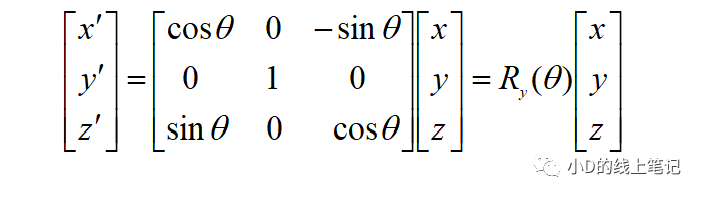
所以,XYZ右手坐标系绕Y轴逆时针旋转θ角的旋转矩阵Ry为:
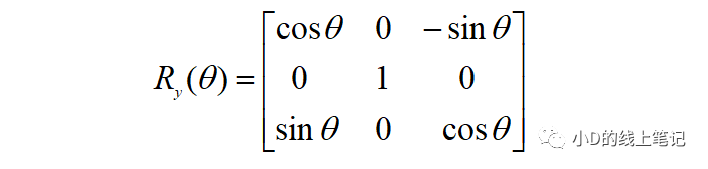
③XYZ右手坐标系绕Z轴逆时针旋转θ角
XYZ右手坐标系绕Z轴逆时针旋转θ的过程如下图所示:
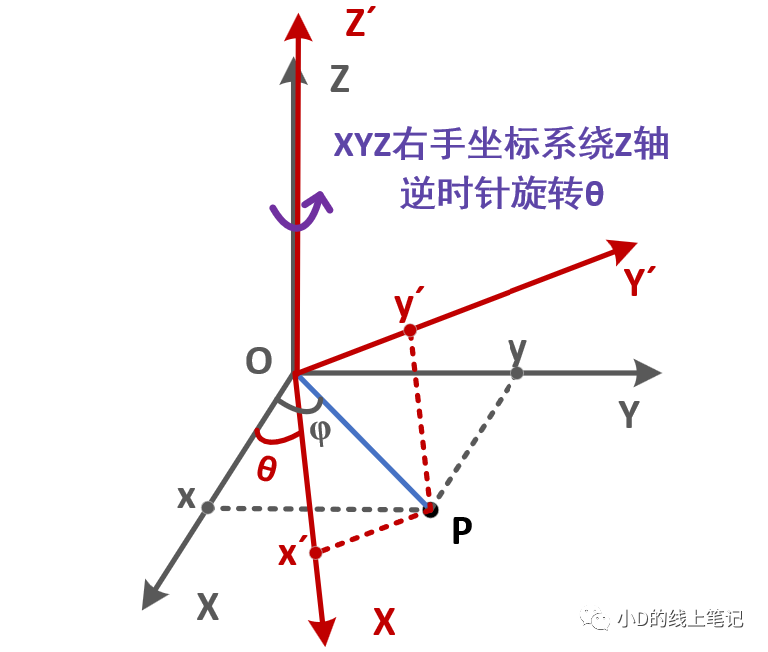
点P在XYZ右手坐标系中的X,Y轴坐标为:
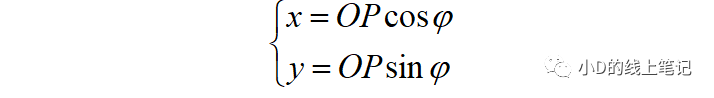
点P在X´Y´Z´坐标系中的x,y坐标为:
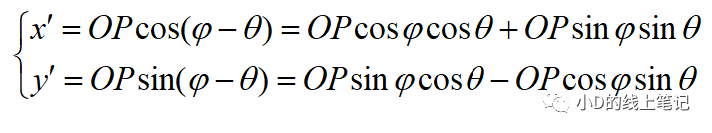
把x,y带入x´,y´中,同时P点在XYZ中的Z轴坐标与其在X´Y´Z´坐标系中的Z´轴坐标是相等的,所以有:
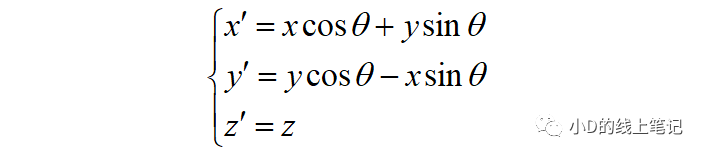
写成矩阵相乘的形式:
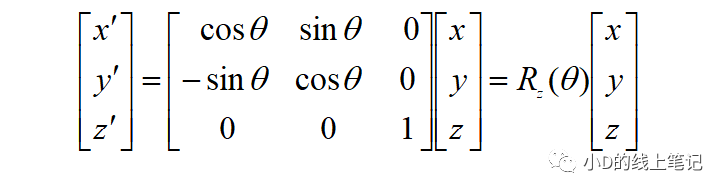
所以,XYZ右手坐标系绕Z轴逆时针旋转θ角的旋转矩阵Rz为:
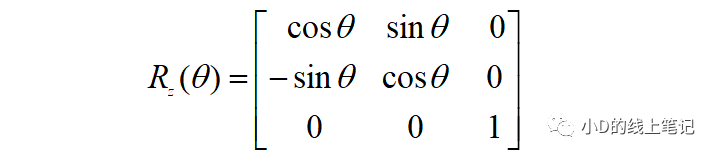
左手坐标系的旋转变换
左手坐标系的旋转过程也是三个,分别是绕X,Y,Z轴旋转,左手坐标系在旋转时,通常规定以顺时针旋转方向为正方向。
①XYZ左手坐标系绕X轴顺时针旋转θ角
XYZ左手坐标系绕X轴顺时针旋转θ角的过程示意图如下所示:
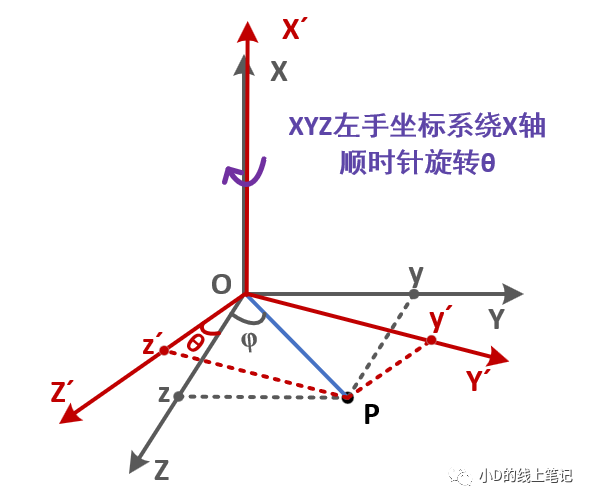
上图中,点P为空间中任意一点,点P保持不动,XYZ左手坐标系绕X轴顺时针旋转θ角形成新的坐标系X´Y´Z´。已知点P在XYZ坐标系中的坐标为(x,y,z),点P在X´Y´Z´中的坐标为(x´,y´,z´),我们要求的是XYZ坐标系变换到X´Y´Z´坐标系这个过程中的旋转矩阵。
从图中可以看出,点P在XYZ坐标系中的Y,Z轴坐标为:
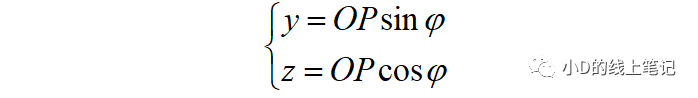
点P在X´Y´Z´坐标系中的Y,Z轴坐标为:
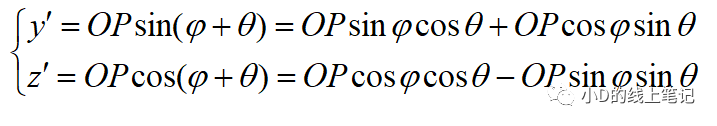
把y,z带入y´,z´中,同时P点在XYZ中的X轴坐标与其在X´Y´Z´中的X´轴坐标是相等的,所以有:
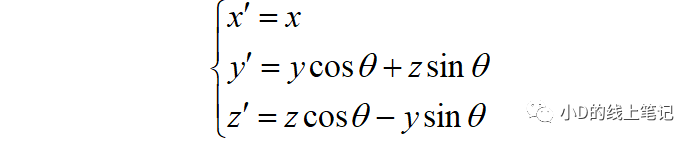
写成矩阵相乘的形式:
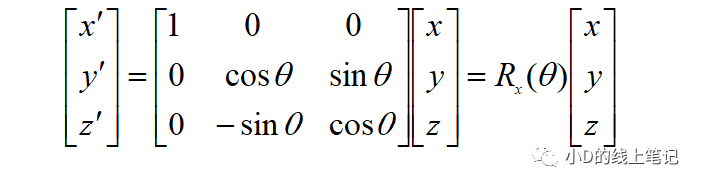
所以,XYZ左手坐标系绕X轴顺时针旋转θ角的旋转矩阵为:
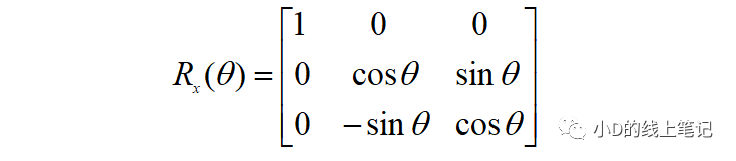
②XYZ左手坐标系绕Y轴顺时针旋转θ角
XYZ左手坐标系绕Y轴顺时针旋转θ角形成X´Y´Z´坐标系,其过程示意图如下所示:
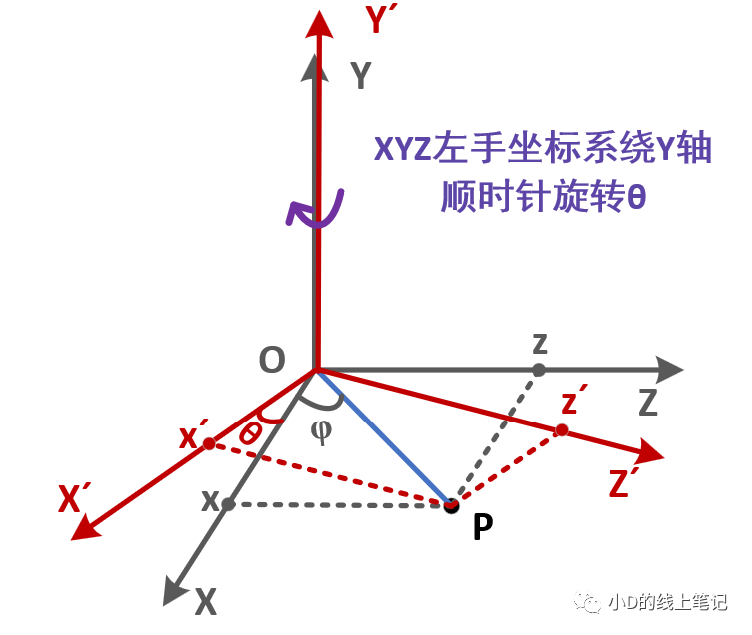
点P在XYZ坐标系中的X,Z轴坐标为:
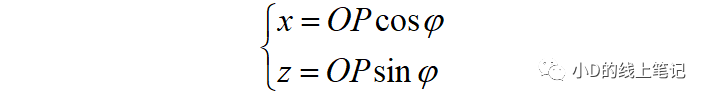
点P在X´Y´Z´坐标系中的X,Z轴坐标为:
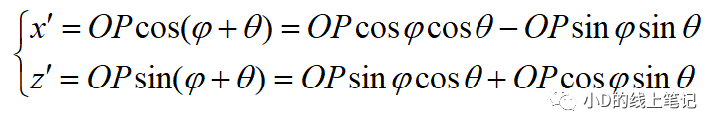
把x,z带入x´,z´中,同时P点在XYZ中的Y轴坐标与其在X´Y´Z´坐标系中的Y´轴坐标是相等的,所以有:
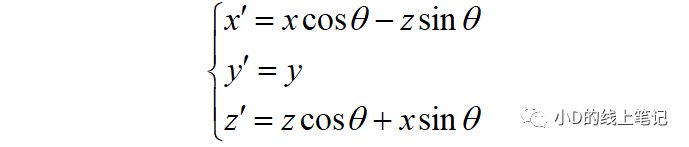
以矩阵形式表示为:
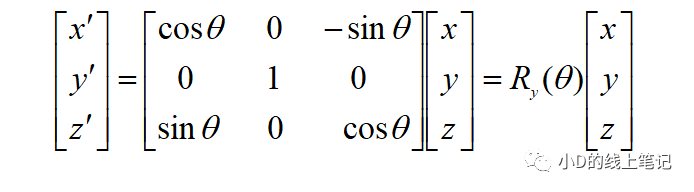
所以,XYZ左手坐标系绕Y轴顺时针旋转θ角的旋转矩阵Ry为:
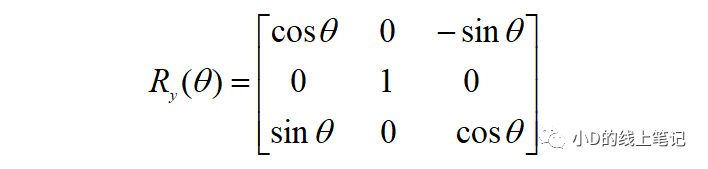
③XYZ左手坐标系绕Z轴顺时针旋转θ角
XYZ左手坐标系绕Z轴顺时针旋转θ角形成X´Y´Z´坐标系的过程示意图如下所示:
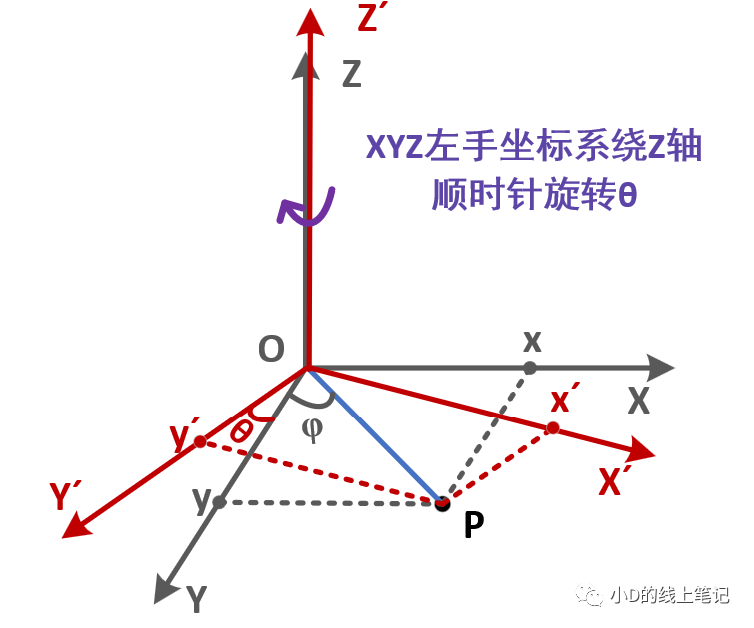
点P在XYZ坐标系中的X,Y轴坐标为:
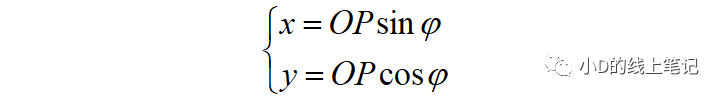
点P在X´Y´Z´坐标系中的X,Y轴坐标为:

把x,y带入x´,y´中,同时P点在XYZ中的Z轴坐标与其在X´Y´Z´坐标系中的Z´轴坐标是相等的,所以有:
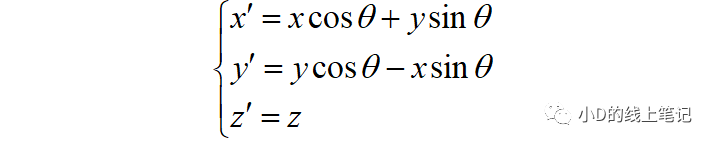
将上式表示成矩阵的形式为:
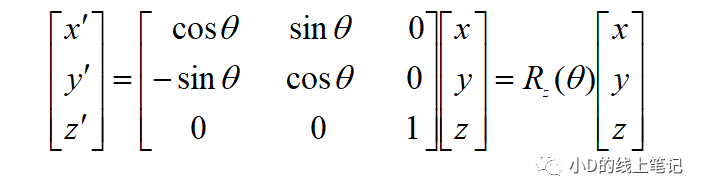
所以,XYZ左手坐标系绕Z轴顺时针旋转θ角的旋转矩阵Rz为:
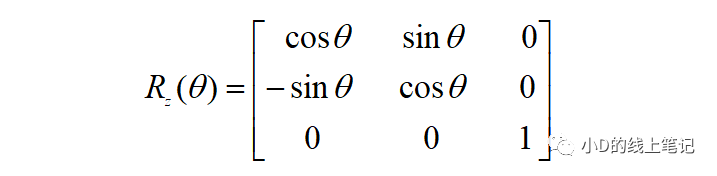
左手坐标系的旋转矩阵到这里就推导完啦。
旋转矩阵的运用
实际中,当我们要推导两个不同的坐标系,比如地心地固坐标系和北东天、北东天坐标系和机体坐标系等坐标系之间的变换关系时,就要用到上面的旋转矩阵。一般的方法是,根据实际的旋转过程,按旋转的先后顺序计算旋转矩阵。
比如对于右手坐标系,如果有一个过程是先绕Y轴逆时针旋转α,再绕X轴顺时针旋转β,最后绕Z轴逆时针旋转γ,那么最终的旋转矩阵的表达就是:
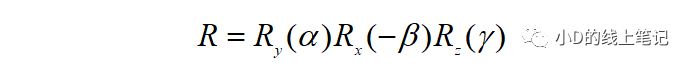
在应用旋转矩阵的过程中,小D还总结了一个经验:不管是左手坐标系还是右手坐标系,假如绕X轴逆时针旋转θ角,相当于绕X轴顺时针旋转2π-θ角,同时也相当于绕X轴顺时针旋转-θ角。
旋转矩阵的验证
推导了这么多公式,那推导结果是否正确呢?我们可以从《雷达数据处理及应用》中找到相关内容:
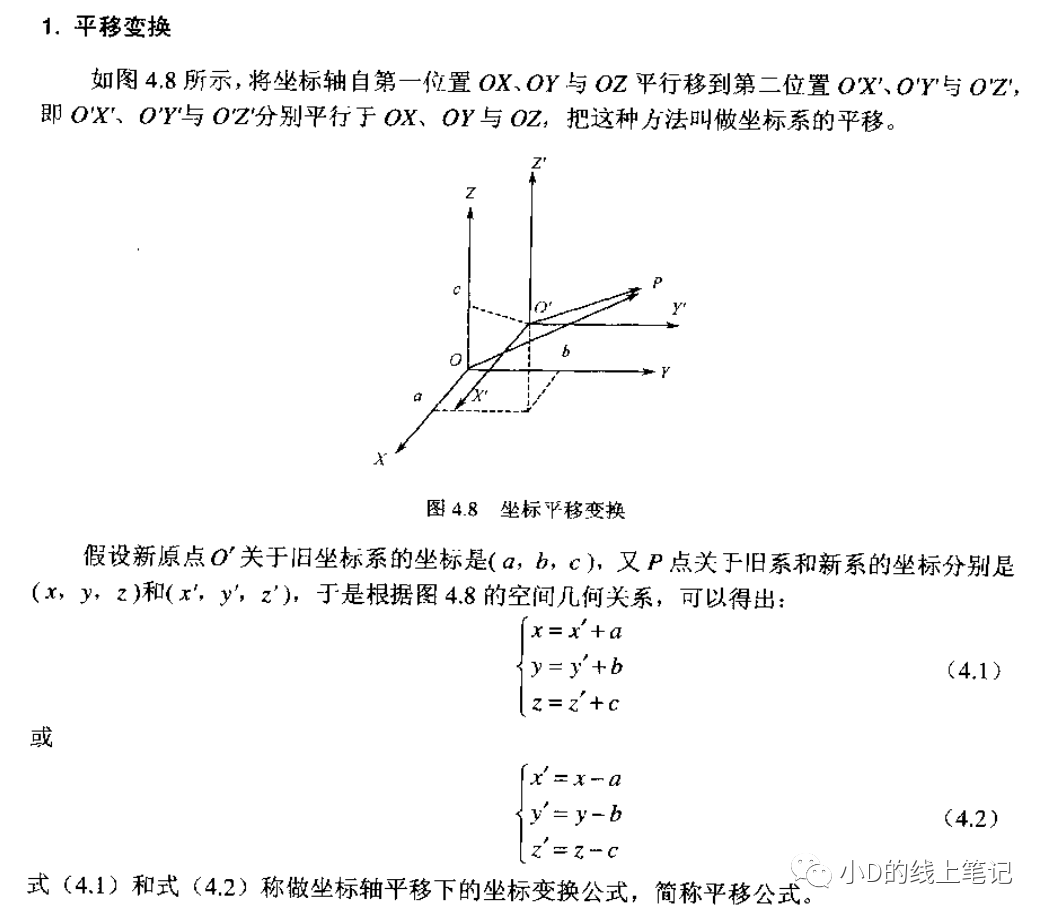


从书中的截图中可以验证,自己推导的平移变换以及右手坐标系的旋转矩阵是没有问题的。但是左手坐标系的推导,小D至今没有找到相关文献,但小D相信肯定是有的。
然后小D向gpt求证,gpt给出的答案是这样的:
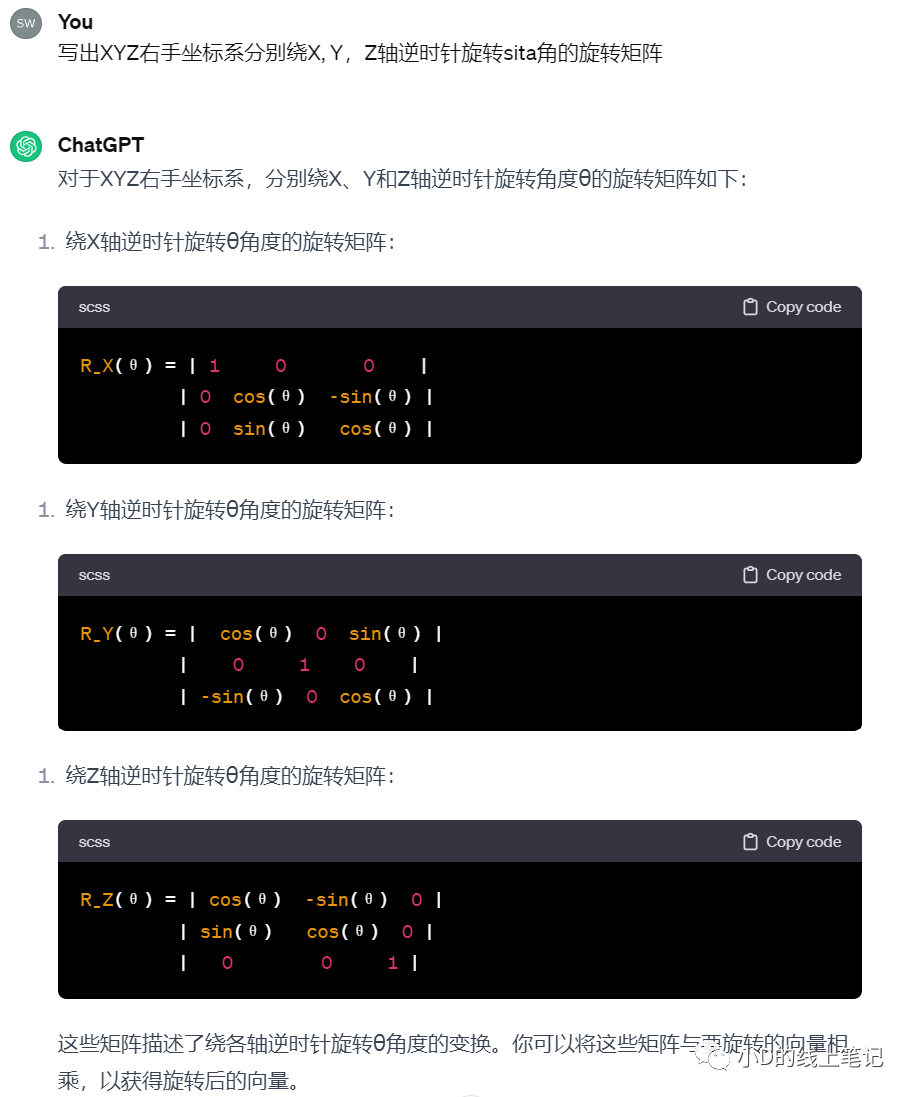
很显然,gpt给出的右手坐标系的旋转矩阵不是小D上面推导的结果,也跟书中的结果不一样。于是小D又去问了gpt4,gpt4的回答是这样的:

gpt4的回答和gpt3.5的回答如出一辙,当时小D心想,gpt脑子估计又瓦特了。直到最近,小D看到了一本英文书籍Geometric Transformations for 3D Modeling_Michael Mortenson,小D才明白,原来gpt是没有正确理解问题,它给出的是坐标系中的点转动,坐标轴不动的情况。这本英文书籍中坐标转换相关的内容是这样的:





这个时候,小D才明白为什么gpt会给出那样的答案,因为旋转分为两种:
①点不动,坐标轴旋转,就是小D推导的公式
②坐标轴不动,点旋转,就是gpt第一次回答的公式
以另一种方式问它,它就回答对了“点不动,坐标轴旋转”的旋转矩阵正确的公式:


到这里,就验证了小D推导的坐标转换的所有公式啦。
审核编辑:汤梓红
-
坐标系
+关注
关注
0文章
29浏览量
7301 -
三维空间
+关注
关注
0文章
17浏览量
7479
原文标题:坐标系的平移、旋转变换——超详细
文章出处:【微信号:FPGA算法工程师,微信公众号:FPGA算法工程师】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
如何使用labview根据XYZ坐标实时绘制三维曲线
电机控制系统中直角坐标系与极坐标系的优势比较,请问TI是否有现成的demo例程?
CAD制图软件新手攻略:坐标系及标注坐标
多电平逆变器三维空间矢量调制
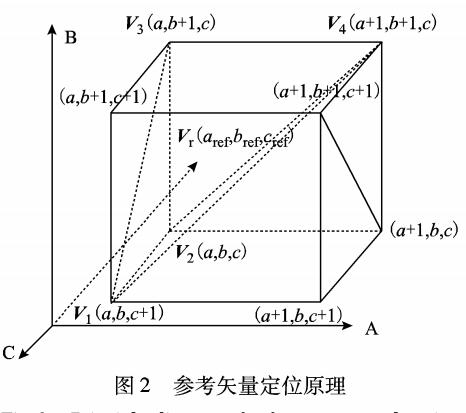
非正交三维坐标系下多电平空间矢量调制策略
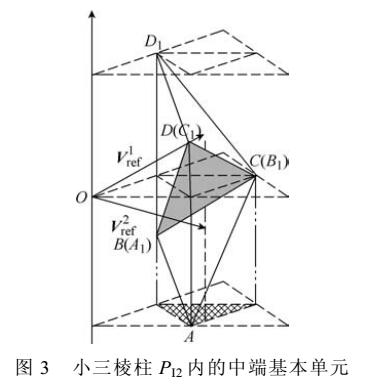
如何使用FPGA实现abc坐标系的三维空间矢量调制算法
立体仓库三维空间路径优化方案的介绍
介绍导航坐标系与载体坐标系之间的姿态旋转矩阵
焊接机器人坐标系有哪几种





 三维空间直角坐标系的平移和旋转变换
三维空间直角坐标系的平移和旋转变换











评论