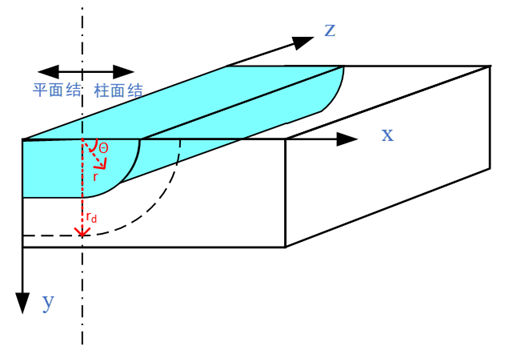
如下图所示为目前国际上最为主流的IGBT芯片俯视图和截面示意图,其中黄色区域代表 型半导体,绿色区域代表
型半导体,绿色区域代表 型半导体。
型半导体。
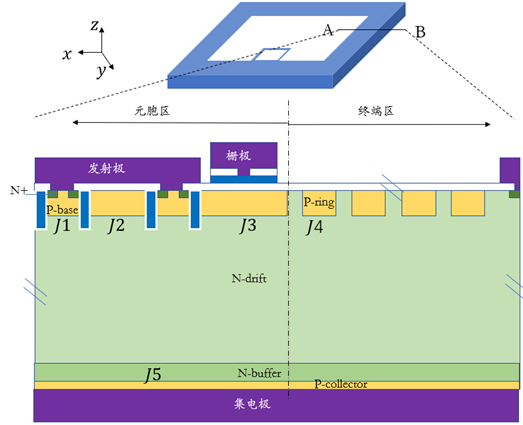
在 平面,IGBT可以划分为元胞区和终端区(后面会详细介绍其作用);z方向又可以划分为芯片正面和芯片背面。
平面,IGBT可以划分为元胞区和终端区(后面会详细介绍其作用);z方向又可以划分为芯片正面和芯片背面。
 平面内可能存在四种类型的PN结,
平面内可能存在四种类型的PN结,
 :处于元胞区,与电极(发射极)相连;
:处于元胞区,与电极(发射极)相连;
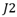 :处于元胞区,与电极不相连;
:处于元胞区,与电极不相连;
 :处于元胞区与终端区的过渡区;
:处于元胞区与终端区的过渡区;
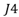 :处于终端区,与电极不相连。
:处于终端区,与电极不相连。
z方向的背面还有一个PN结,
 :处于芯片背面,与电极(集电极)相连。
:处于芯片背面,与电极(集电极)相连。
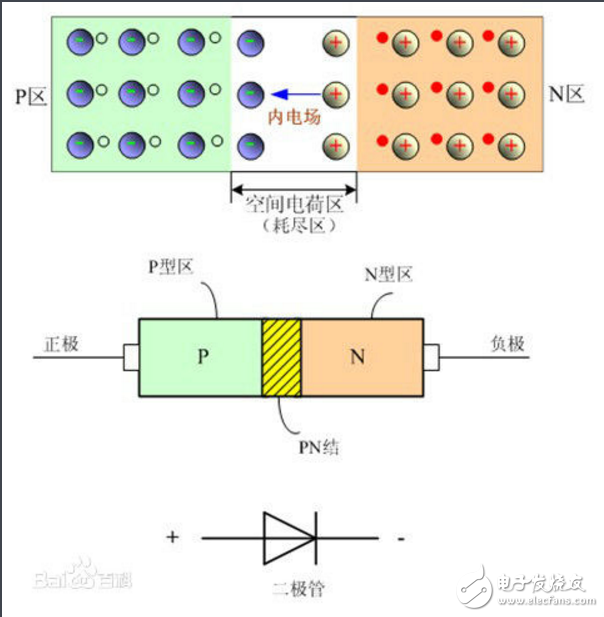
在理解IGBT内部的若干PN结如何协作之前,我们先看单个PN结是如何工作的。第二章中,我们阐述了热平衡状态下的PN结存在一个内部势垒,阻碍PN结两侧的多子(P型中的空穴和N型中的电子)向对方扩散。
显然,若要促进多子能够进一步扩散,就必须克服这个势垒,所采用的办法就是在P区施加一个正向电压,以形成一个与内建电场相反方向的电场;反之,若要进一步阻碍多子扩散,也可以通过在N区施加一个正向电压,从而增加PN结的内部势垒。这两个状态分别对应PN结的导通状态和阻断状态。
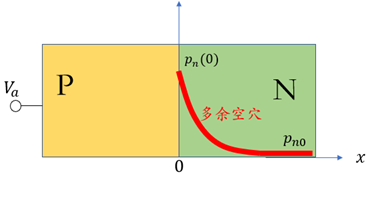
如下图所示的一个PN结,假设P区掺杂浓度为 ,N区掺杂浓度为
,N区掺杂浓度为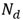 。P区因为部分空穴扩散到N区而有部分区域带负电,其宽度用
。P区因为部分空穴扩散到N区而有部分区域带负电,其宽度用 表示;反之N区因为部分电子扩散到P区而有部分区域带正电,其宽度用
表示;反之N区因为部分电子扩散到P区而有部分区域带正电,其宽度用 表示。
表示。
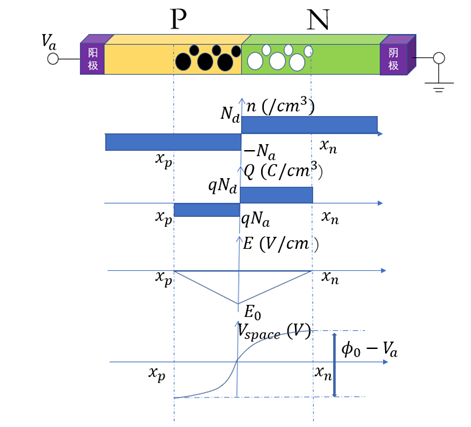
原本都处于电中性的P区和N区,因为多子扩散,在相交的PN结区域分别有部分空间带电了,这个空间被称为“空间电荷区”,又被称为“耗尽区”,其宽度为: (
( 为depletion的缩写)。
为depletion的缩写)。
定义P型半导体所连接电极为阳极,对应的N型半导体所连接电极为阴极。假设阳极施加的外界电压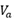 为负,那么感生的电场方向由N型指向P型,显然会增强PN结的内建电场,使得耗尽区边界处的多子在电场作用下漂移至对面,留下更大的空间电荷区;同时增大的内建电场会进一步阻碍多子扩散。这个过程可以用静电学的高斯定律和泊松方程进行描述,
为负,那么感生的电场方向由N型指向P型,显然会增强PN结的内建电场,使得耗尽区边界处的多子在电场作用下漂移至对面,留下更大的空间电荷区;同时增大的内建电场会进一步阻碍多子扩散。这个过程可以用静电学的高斯定律和泊松方程进行描述,

其中, 表示空间电荷密度,
表示空间电荷密度, 表示介电常数,
表示介电常数, 表示电势差。两个方程的物理意义是:有电荷存在的地方,就会存在电场,其方向为正电荷指向负电荷;而电场在空间的积分就是电势。所以,空间电荷区会存在N区(正电)指向P区(负电)的电场。因此当外加电压
表示电势差。两个方程的物理意义是:有电荷存在的地方,就会存在电场,其方向为正电荷指向负电荷;而电场在空间的积分就是电势。所以,空间电荷区会存在N区(正电)指向P区(负电)的电场。因此当外加电压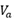 为正,感生与原来向反方向的电场,那么空间电荷区变窄,内建电场减弱,PN结导通;反之,当外加电压
为正,感生与原来向反方向的电场,那么空间电荷区变窄,内建电场减弱,PN结导通;反之,当外加电压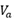 为负,感生与原来相同方向的电场那么空间电荷区变宽,内建电场增强,PN结就可以承受更高的电势,直到电场峰值
为负,感生与原来相同方向的电场那么空间电荷区变宽,内建电场增强,PN结就可以承受更高的电势,直到电场峰值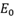 材料的临界击穿电场。这就是IGBT能承受高电压的原因。
材料的临界击穿电场。这就是IGBT能承受高电压的原因。
进一步地,根据高斯定律和泊松方程,电势的梯度正比于电场强度,而电场的梯度正比于空间电荷区的浓度。显然当外加电压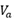 为负,空间电荷区浓度越低,那么电场衰减越慢,相应
为负,空间电荷区浓度越低,那么电场衰减越慢,相应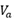 所对应的耗尽区就越宽,达到临界电场强度
所对应的耗尽区就越宽,达到临界电场强度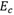 所对应的
所对应的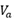 绝对值就越高,也就是可承受电压越高。这就是为何电压等级越高的IGBT,其衬底浓度需要越低的缘故。
绝对值就越高,也就是可承受电压越高。这就是为何电压等级越高的IGBT,其衬底浓度需要越低的缘故。
下面简要推导PN结阻断状态下的峰值电场强度、耗尽区宽度与掺杂浓度以及外加电压之间的关系。
引用高斯定理的积分形式:
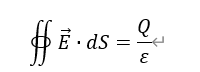
即电场沿闭合空间的积分正比于其内部电荷之和。
如下图所示,将闭合四边形的四边分别标记为,
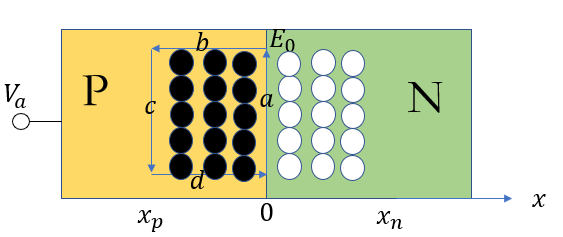
显然,1.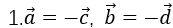 ,因此电场在
,因此电场在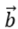 和
和 方向的积分相互抵消;
方向的积分相互抵消;
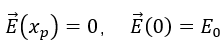 ;
;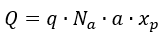 ;
;
因此,
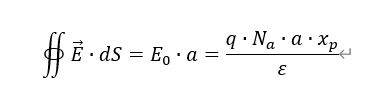
所以,

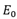 的表达式中利用了平衡态下的电中性原理,即,
的表达式中利用了平衡态下的电中性原理,即,

当半导体为均匀掺杂时(绝大多数都是这种情况,但也有例外,如经扩散而形成的高斯分布掺杂,后面讲到工艺时会进一步分析),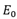 随空间线性变化,其在耗尽区内的积分即为PN结两侧的电势差,即
随空间线性变化,其在耗尽区内的积分即为PN结两侧的电势差,即

其中, 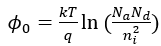 ,内建电势
,内建电势
综上可以推算出P区和N区内耗尽区的宽度分别为:

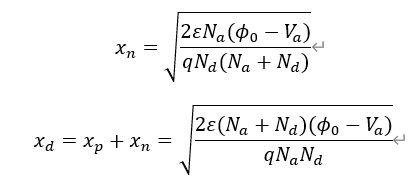
当半导体为非均匀掺杂时,推算过程相同,但稍微繁杂一些。
举例:以Si为例,假设P型掺杂浓度为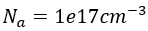 ,N型掺杂浓度为
,N型掺杂浓度为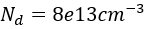 ,
, ,
,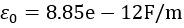 ,
,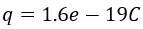 ,计算
,计算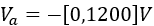 的耗尽区宽度变化趋势。
的耗尽区宽度变化趋势。 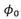 相对
相对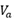 的绝对值是个小量,计算过程中可以忽略掉,或者以0.7V替换。
的绝对值是个小量,计算过程中可以忽略掉,或者以0.7V替换。
计算结果如下图所示。
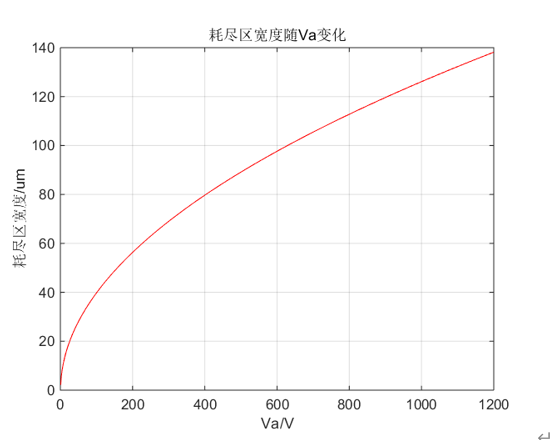
可以看出,承受1200V的电压,大约需要140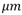 的厚度。
的厚度。
-
半导体
+关注
关注
334文章
27323浏览量
218328 -
IGBT
+关注
关注
1267文章
3790浏览量
248940 -
PN结
+关注
关注
8文章
481浏览量
48720 -
集电极
+关注
关注
4文章
214浏览量
22176 -
igbt芯片
+关注
关注
0文章
32浏览量
5154
发布评论请先 登录
相关推荐
PN结的电容特性
pin结与pn结的特性比较
PN结的原理/特征/伏安特性/电容特性
pn结静电特性
pn结的特性,PN结的击穿特性,PN结的电容特性





 IGBT中都有哪些PN结?PN结的组合会给IGBT带来哪些特性?
IGBT中都有哪些PN结?PN结的组合会给IGBT带来哪些特性?
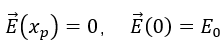 ;
;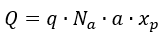 ;
;










评论