根据前面的分析,电子或者空穴产生于导带和价带中是一个统计概率,这个概率符合费米分布规律。
所以虽然前文推导出了在某个能级的电荷浓度准确表达式,但实际上这是一个统计算法,其描述的是一个动态平衡过程。具体到每一个能级及其相应的能态,则是电子在不断的产生和消失的过程中处于平衡状态。
这个过程与环境温度和材料本身的性质相关,教科书中通常将这个过程理解为:由于热运动,电子获得能量而激发到能量更高的能级;但电子彼此碰撞、或者与晶格碰撞等过程失去能量又回到能量更低的能级,这个过程持续往复。
更进一步地,考虑半导体中掺入了某种杂质、或者引入了某种缺陷的情况。杂质或缺陷的引入导致在禁带之中形成了局域的能级,因为这些能级相较导带及价带的能级离费米能级更近,所以电子占有概率更大。同时,因为能态密度较低,占据这些能级的电子是不能自由运动的,表现为电荷减少,被“复合”了。
结合质量守恒定律,有一种理解方式如下:材料自身在单位体积内能够提供的电子数量是一定的,假设一个原子提供一个电子,那么材料可以提供的总电子数量即为


当占据杂质或缺陷能级消耗了一部分电子,那么激发到导带上的电子自然少了,表现为电子被杂质或缺陷能级复合了。
事实上,若要严谨推导半导体中掺杂后的复合现象,还是要从杂质引入所导致的能级变化和能态变化来分析电子占据不能能级的概率,这里不做延展推导。
想要说明的是,类似空穴是人们抽象出来的一个概念一样,“复合”也可以当做人们抽象出来的一个概念,是相对“产生”而言,其本质还是因为某种原因如掺杂、缺陷等,导致能级和/或能态发生变化,导致电子在不同能级进行重新分布。
假如电子进入导带,能级分布密集,能态很多,且基本没有电子占据,那么 电子只需获得很小的能量即可进入另外一个能态,电子占据这些能态后可以自由移动,表现为自由电荷的产生 。
假如进入杂质或缺陷能级,能态很少,电子需获得较大的能量才可进入另外一个能态,那么电子占据这些能态后不能自由移动,表现为自由电荷的复合。
既然引入了复合的概念,那就应该有复合的寿命,定义为τ,这个寿命是如何得来,又是如何变化的,下面简要推导。



显然净复合率U还可表达为

对照U的两个表达式,可以得出电荷寿命

根据这个表达式,随着新增电荷数的增加,电荷寿命会降低,所以 半导体大注入情况下比小注入情况下的寿命要小,IGBT工作通常处于大注入状态。IGBT关断过程中的拖尾电流通常取决于存储的电荷及其寿命。
对于本征半导体,∆n=∆p=0,n 0 =p 0 =n i ,定义其载流子寿命为

对于p型掺杂半导体,p 0 >>n 0 ,这个浓度显然是 仅与温度相关的常数,不随时间变化, 因为∆n=∆p,所以

两边对时间求导,且dp 0 /dt=dn 0 /dt=0

显然上式成立的条件是τ p <<τ n ,即空穴寿命远小于电子寿命。所以对于p型掺杂半导体可以仅考虑少子电子,其寿命为

同理,对于n型掺杂半导体,空穴为少子,其寿命为

显然掺杂后的少子寿命都是要小于本征半导体的载流子寿命的。
-
半导体
+关注
关注
334文章
27183浏览量
217710 -
IGBT
+关注
关注
1265文章
3783浏览量
248691 -
电荷
+关注
关注
1文章
622浏览量
36127 -
载流子
+关注
关注
0文章
134浏览量
7649
发布评论请先 登录
相关推荐
[专]电荷为何自发产生——第一弹
一种新型低电荷共享电荷泵电路
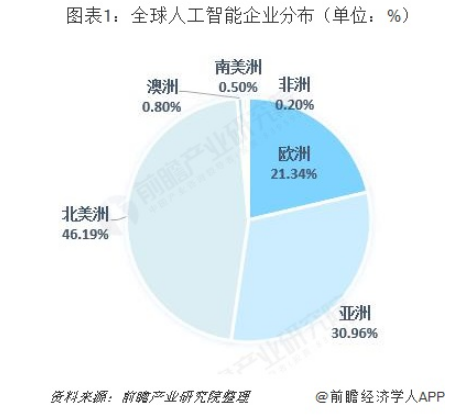
一文带你解读全球人工智能产业发展现状
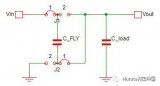
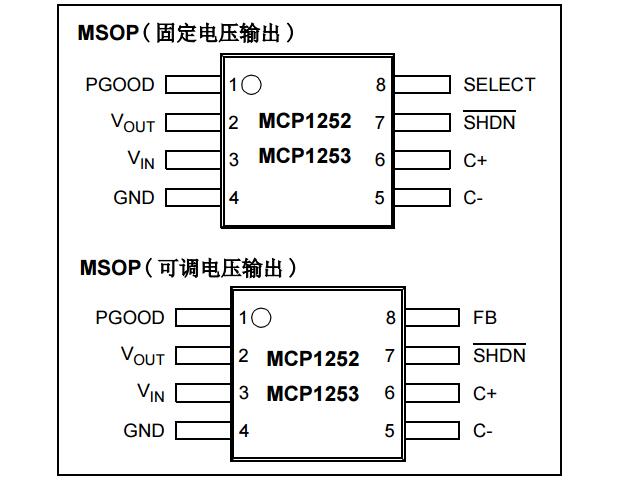
一文解析什么是电荷泵电源
电容器存储电荷的原理是怎样的(一)
一文解读FPGA设计者的5项基本功及设计流程资料下载





 一文解读电荷的复合
一文解读电荷的复合











评论