堆的实现思路
什么是堆？
- 堆是一种 基于树结构的数据结构，它是一棵二叉树 ，具有以下两个特点：
- 堆是一个完全二叉树，即除了最后一层，其他层都是满的，最后一层从左到右填满。
- 堆中每个节点都满足堆的特性，即父节点的值要么等于或者大于（小于）子节点的值。
1.1 堆的分类
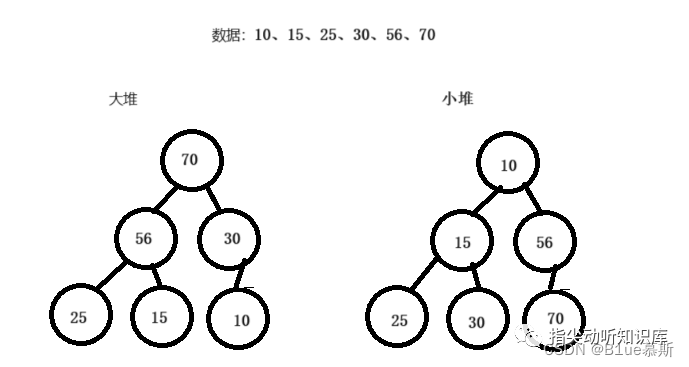
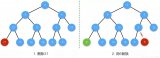
堆一般分为两类： 大堆和小堆 。
- 大堆中，父节点的值大于或等于子节点的值，
- 小堆中，父节点的值小于或等于子节点的值。
堆的主要应用是在排序和优先队列中。
以下分别为两个堆（左大堆，右小堆）：
Part2 堆的实现思路
2.1 使用什么实现？
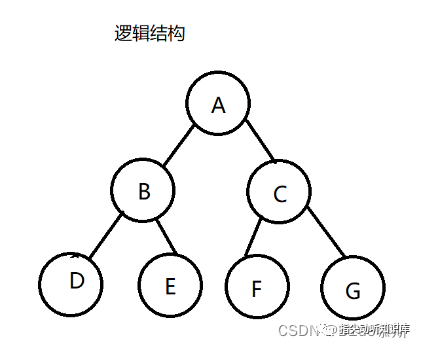
逻辑结构如上， 然而这仅仅是我们想像出来的而已，而实际上的堆的物理结构是一个完全二叉树 ， 通常是 用数组实现的 。如下：
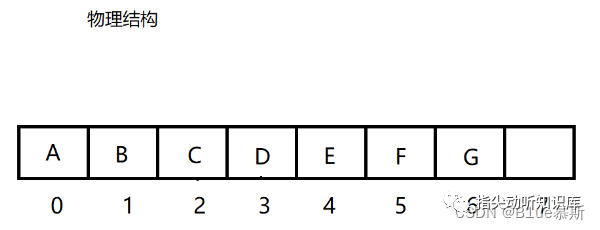
对此，这就要引申出一个问题？我们该如何分辨父节点以及子节点呢？如下：
2.2 怎么分辨父节点以及子节点？
通常我们的数组下标为“0”处即为根节点，也就是说我们一定知道一个父节点！并且我们也有“计算公式”来计算父节点以及子节点。（先记住，后面实现有用！！！）也就是说我们也可以通过公式从每一个位置计算父节点以及子节点！如下：
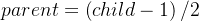
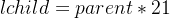
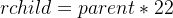
2.3 总体实现思路
先建立一个结构体，由于堆的结构实际上是一颗完全二叉树，因此我们的 结构跟二叉树一样即可！ 接着，想想我们的堆需要实现的功能？ 构建、销毁、插入、删除、取堆顶的数据、取数据个数、判空 。(⊙o⊙)…基本的就这些吧哈~
接着按照 定义函数接口->实现各个函数功能->测试测试->收工(-_^) o( ￣▽￣ )ブ
Part3** 堆的实现**
3.1 结构体以及接口的实现
typedefint HPDataType;
typedefstruct Heap
{
HPDataType* _a;
int _size;
int _capacity;
}Heap;
// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);
3.2 堆的两种建堆方式
在实现以上的接口之前，我们必须要知道堆的两种建堆方式！！！
并且仅仅通过调整建堆方式的<和>符号，我们就可以轻易控制大小堆，具体看代码注释！
建堆有两种方式，分别是 自底向上建堆以及自顶向下建堆。 具体简介如下：
- 自底向上建堆：自底向上建堆是指按照原始数组顺序依次插入元素，然后对每个插入的元素执行向上调整的操作，使得堆的性质保持不变。这种方法需要对每个元素都进行调整操作，时间复杂度为 O(nlogn)。
- 自顶向下建堆：自顶向下建堆是指从堆顶开始，对每个节点执行向下调整操作，使得堆的性质保持不变。这种方法需要从根节点开始递归向下调整，时间复杂度为 O(n)。因此，自顶向下建堆的效率比自底向上建堆要高。
以上两种建堆方式，实际上是基于两种调整方法，接下来将详细介绍：
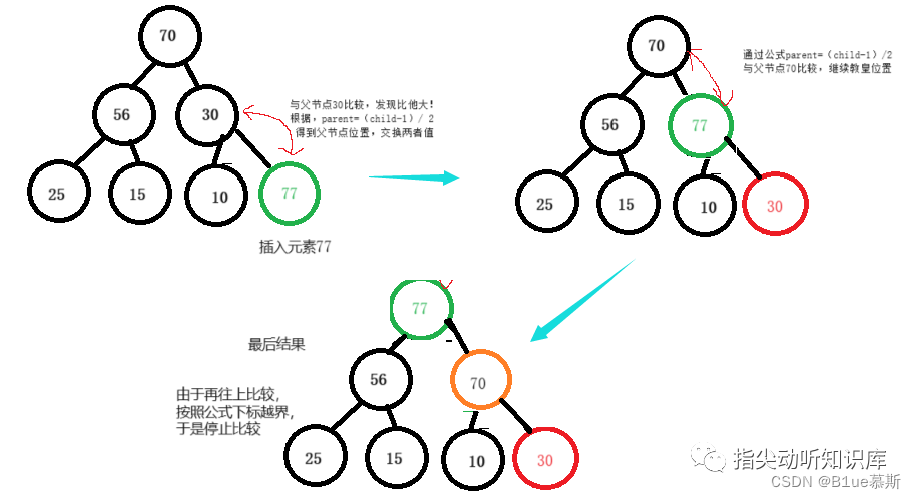
向上调整方法
堆的向上调整方法将新插入的节点从下往上逐层比较，如果当前节点比其父节点大（或小，根据是大根堆还是小根堆），则交换这两个节点。一直向上比较，直到不需要交换为止。这样可以保证堆的性质不变。
具体步骤如下：
- 将新插入的节点插入到堆的最后一位。
- 获取该节点的父节点的位置，比较该节点与其父节点的大小关系。
- 如果该节点比其父节点大（或小，根据是大根堆还是小根堆），则交换这两个节点。
- 重复步骤2-3，直到不需要交换为止，堆的向上调整完成。
- 堆的向上调整的时间复杂度为O(logn)，其中n为堆的大小。
一图让你了解~：
实现如下：
void swap(HPDataType* s1, HPDataType* s2)
{
HPDataType temp = *s1;
*s1 = *s2;
*s2 = temp;
}
void Adjustup(HPDataType* a, int child)//向上调整
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] > a[parent])//建大堆，小堆则<
{
swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
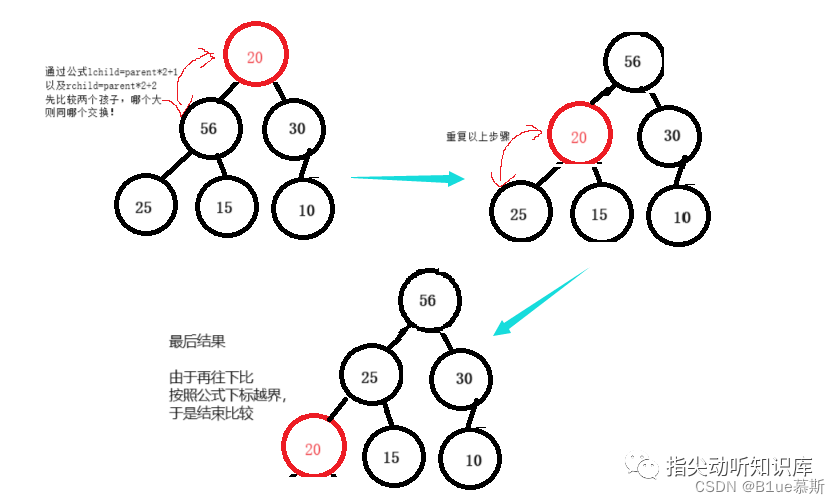
向下调整方法
堆的向下调整方法是指将某个节点的值下放至其子节点中，以维护堆的性质的过程。
假设当前节点为 i，其左子节点为 2i+1，右子节点为 2i+2，堆的大小为 n
则向下调整的步骤如下：
- 从当前节点 i 开始，将其与其左右子节点中较小或较大的节点比较，找出其中最小或最大的节点 j。
- 如果节点 i 小于等于（或大于等于，取决于是最小堆还是最大堆）节点 j，则说明它已经满足堆的性质，调整结束；否则，将节点 i 与节点 j 交换位置，并将当前节点 i 更新为 j。
- 重复执行步骤 1 和步骤 2，直到节点 i 没有子节点或已经满足堆的性质。
一图让你了解~：
实现如下：
void swap(HPDataType* s1, HPDataType* s2)
{
HPDataType temp = *s1;
*s1 = *s2;
*s2 = temp;
}
void Adjustdown(HPDataType* a, int n, int parent)//向下调整
{
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && a[child + 1] > a[child])//找出两个孩子中较大的那个，此为大堆，如果要实现小堆则 改 >
{
++child;
}
if (a[child] > a[parent])//此为大堆，如果要实现小堆则 改 >
{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
3.3 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n)
{
assert(hp);
assert(a);
hp- >_a = (HPDataType*)malloc(sizeof(HPDataType) * n);
if (!hp- >_a)
{
perror("malloc fail");
exit(-1);
}
hp- >_capacity = hp- >_size = n;
//将a中的元素全部转移到堆中
memcpy(hp- >_a, a, sizeof(HPDataType) * n);
//建堆
for (int i = 1; i < n; i++)
{
Adjustup(hp- >_a, i);//按向上调整，此建立大堆
}
}
本文的构建方法是 通过传递一个数组以及传递一个数组大小来构建的 ，里面包括了堆结构体的初始化操作，基本的建堆方式则是通过向上调整方法建堆。
3.4 堆的销毁
void HeapDestory(Heap* hp)
{
assert(hp);
free(hp- >_a);
hp- >_a = NULL;
hp- >_capacity = hp- >_size = 0;
}
就正常的销毁操作？大家应该都懂（确信） (o°ω°o)
3.5 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{
assert(hp);
if (hp- >_capacity == hp- >_size)//扩容
{
int newcapacity = hp- >_capacity == 0 ? 4 : hp- >_capacity * 2;
HPDataType* new = (HPDataType*)realloc(hp- >_a, sizeof(HPDataType) * newcapacity);
if (!new)
{
perror("realloc fail");
exit(-1);
}
hp- >_a = new;
hp- >_capacity = newcapacity;
}
hp- >_a[hp- >_size++] = x;
Adjustup(hp- >_a, hp- >_size - 1);
}
实现是对于堆的空间进行判断，不够则是扩容操作，当然也有初始化的意思，接着是通过向上调整的方式插入操作。
3.6 堆的删除（较重要）
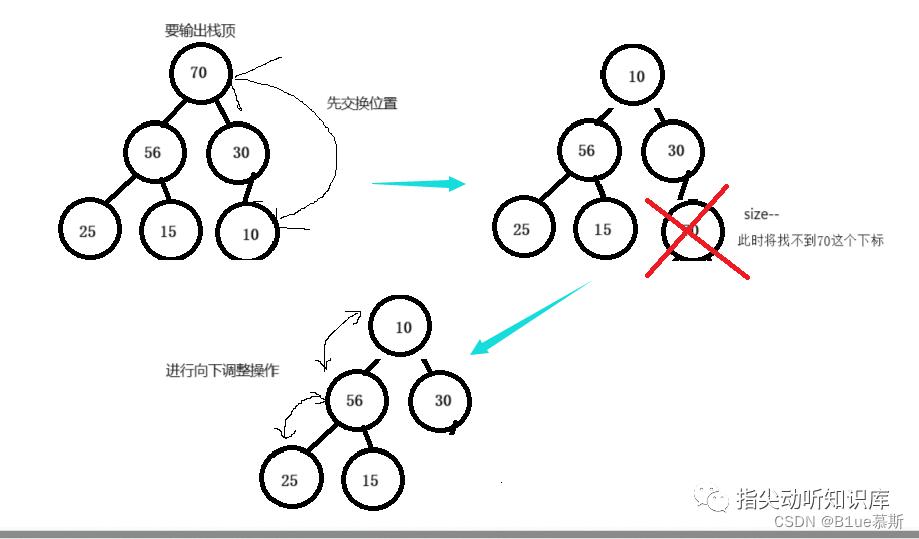
void HeapPop(Heap* hp)//先将最后一个数与堆顶交换，然后再让size--，再进行向下调整
{
assert(hp);
swap(&hp- >_a[0], &hp- >_a[hp- >_size - 1]);
hp- >_size--;
Adjustdown(hp- >_a, hp- >_size, 0);
}
进行删除操作，我们当然是删除堆顶啦，这个删除操作先将最后一个数与堆顶交换，然后再让size--，再进行向下调整。
一图让你了解~：
3.7 取堆顶的数据
HPDataType HeapTop(Heap* hp)//取堆顶
{
assert(hp);
assert(hp- >_size > 0);
return hp- >_a[0];
}
3.8 堆的数据个数
int HeapSize(Heap* hp)//堆大小
{
assert(hp);
return hp- >_size;
}
3.9 堆的判空
int HeapEmpty(Heap* hp)//判堆空
{
assert(hp);
return hp- >_size==0;
}
Part4 总体代码
4.1pile.h
#pragma once
#define _CRT_SECURE_NO_WARNINGS 01
#include< stdio.h >
#include< stdlib.h >
#include< string.h >
#include< assert.h >
typedefint HPDataType;
typedefstruct Heap
{
HPDataType* _a;
int _size;
int _capacity;
}Heap;
// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);
4.2pile.c
#include"pile.h"
void swap(HPDataType* s1, HPDataType* s2)
{
HPDataType temp = *s1;
*s1 = *s2;
*s2 = temp;
}
void Adjustup(HPDataType* a, int child)//向上调整
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] > a[parent])//建大堆，小堆则<
{
swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void Adjustdown(HPDataType* a, int n, int parent)//向下调整
{
int child = parent * 2 + 1;
while (child < n)
{
if (child + 1 < n && a[child + 1] > a[child])//找出两个孩子中较大的那个，此为大堆，如果要实现小堆则 改 >
{
++child;
}
if (a[child] > a[parent])//此为大堆，如果要实现小堆则 改 >
{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void HeapCreate(Heap* hp, HPDataType* a, int n)
{
assert(hp);
assert(a);
hp- >_a = (HPDataType*)malloc(sizeof(HPDataType) * n);
if (!hp- >_a)
{
perror("malloc fail");
exit(-1);
}
hp- >_capacity = hp- >_size = n;
//将a中的元素全部转移到堆中
memcpy(hp- >_a, a, sizeof(HPDataType) * n);
//建堆
for (int i = 1; i < n; i++)
{
Adjustup(hp- >_a, i);//按向上调整，此建立大堆
}
}
void HeapDestory(Heap* hp)
{
assert(hp);
free(hp- >_a);
hp- >_a = NULL;
hp- >_capacity = hp- >_size = 0;
}
void HeapPush(Heap* hp, HPDataType x)
{
assert(hp);
if (hp- >_capacity == hp- >_size)//扩容
{
int newcapacity = hp- >_capacity == 0 ? 4 : hp- >_capacity * 2;
HPDataType* new = (HPDataType*)realloc(hp- >_a, sizeof(HPDataType) * newcapacity);
if (!new)
{
perror("realloc fail");
exit(-1);
}
hp- >_a = new;
hp- >_capacity = newcapacity;
}
hp- >_a[hp- >_size++] = x;
Adjustup(hp- >_a, hp- >_size - 1);
}
void HeapPop(Heap* hp)//先将最后一个数与堆顶交换，然后再让size--，再进行向下调整
{
assert(hp);
swap(&hp- >_a[0], &hp- >_a[hp- >_size - 1]);
hp- >_size--;
Adjustdown(hp- >_a, hp- >_size, 0);
}
HPDataType HeapTop(Heap* hp)//取堆顶
{
assert(hp);
assert(hp- >_size > 0);
return hp- >_a[0];
}
int HeapSize(Heap* hp)//堆大小
{
assert(hp);
return hp- >_size;
}
int HeapEmpty(Heap* hp)//判堆空
{
assert(hp);
return hp- >_size==0;
}
4.3test.c
#include"pile.h"
void test()
{
Heap hp;
int arr[] = { 1,6,2,3,4,7,5 };
HeapCreate(&hp, arr, sizeof(arr) / sizeof(arr[0]));
//HeapPush(&hp, 10);
printf("%dn", HeapSize(&hp));
while (!HeapEmpty(&hp))
{
printf("%d %d n", HeapTop(&hp), HeapSize(&hp));
HeapPop(&hp);
}
printf("%dn", HeapSize(&hp));
HeapDestory(&hp);
HeapSort(arr, sizeof(arr) / sizeof(arr[0]));
printf("n");
}
int main()
{
test();
return0;
}
4.4 测试结果
声明：本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人，不代表电子发烧友网立场。文章及其配图仅供工程师学习之用，如有内容侵权或者其他违规问题，请联系本站处理。
举报投诉
-
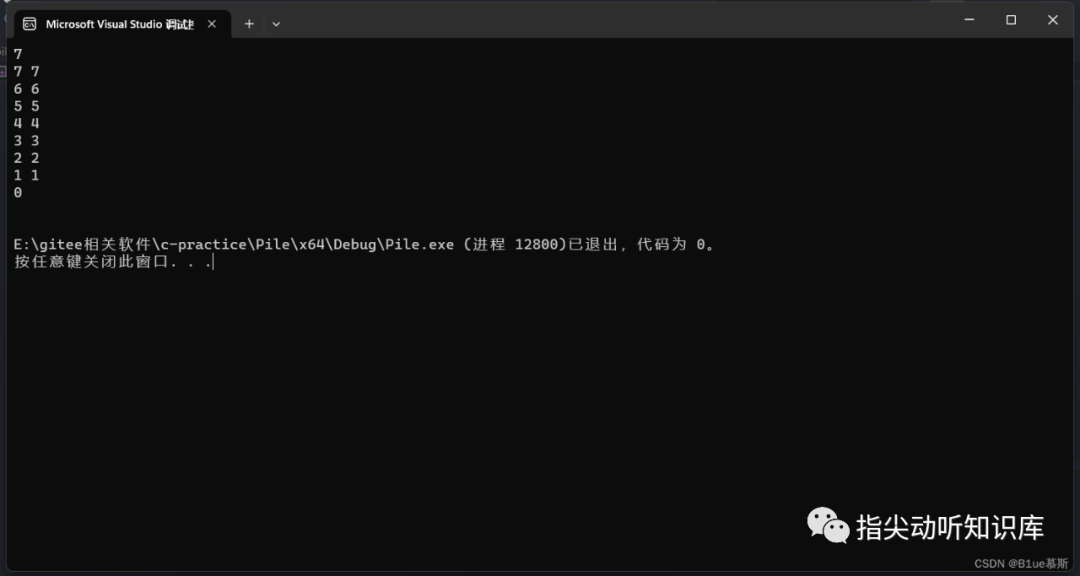
接口
+关注
关注
33文章
8580浏览量
151047 -
数据结构
+关注
关注
3文章
573浏览量
40124 -
元素
+关注
关注
0文章
47浏览量
8429 -
二叉树
+关注
关注
0文章
74浏览量
12324
发布评论请先 登录
相关推荐
堆煤传感器的工作原理是什么？
堆煤传感器正常时煤位传感器输出端“堆煤”输出高电平，当煤位增高推移传感器偏转一定角度时，其内万向接点导通， “堆煤”输出低电平，“满煤”指示灯亮，经短暂延时，主机执行继电器释放，实现
发表于 03-31 09:00
如何使用链接脚本删除堆分配？
的 heap_symbol），这对我来说会更好，因为否则这个符号会得到它的地址，并且可以使用它的地址覆盖内存。我的问题是，当我只是丢弃它时，我得到了期望此引用的 gcc 文件 (_cr_sbrk.c) 的引用错误。我想寻求帮助来实现我的目标，即安全地从链接器中删除堆分配
发表于 03-23 07:05
整流堆,什么是整流堆
整流堆,什么是整流堆
桥堆的检测
1. 全桥的检测 大多数的整流全桥上，均标注有“+”、“-”、“~”符号（其中“+”为整流后输出电压
发表于 02-27 10:46
•2142次阅读
串口WiFi模块实现远程控制电饭煲的设计思路分享.pdf
分享一个串口WiFi模块实现远程控制电饭煲的设计思路，通过串口wifi模块可以在手机app上远程操控电饭煲，相比定时的效果更好！
发表于 04-26 16:57
•76次下载
什么是堆内存？堆内存是如何分配的？
在一般的编译系统中，堆内存的分配方向和栈内存是相反的。当栈内存从高地址向低地址增长的时候，堆内存从低地址向高地址分配。
实现完全 MCU 分区隔离：堆
曾几何时，嵌入式系统非常简单以至于很少使用堆。然而，从那时起，复杂性增长得如此之快，以至于大多数嵌入式系统，甚至是实时操作系统，现在都使用堆。如果只有一个堆在使用，堆效率就不是什么大问
发表于 11-26 15:21
•20次下载
桥堆的作用是什么？桥堆整流后电压是多少?
桥堆的作用及工作原理解读 桥堆的作用是什么？桥堆整流后电压是多少? 桥堆是一种常用的电路，广泛应用于电力电子系统中。桥堆是一种全波整流电路
UVC bulk传输实现思路
前段时间有个读者咨询UVC bulk 传输实现，接着这个机会重新梳理一遍UVC bulk 传输实现思路,同时对比ISO 与 Bulk 实现不同。
如何使用SystemView的堆监控功能
SystemView能够监视应用程序如何使用动态存储。这意味着，如果应用程序中使用了C或C++堆、自定义堆或RTOS提供的内存池对象，我们可以跟踪这些对象的使用情况。SystemView可以在一个
工商网监
评论