机器人在执行期望目标任务时,我们希望机器人能精确地达到人类所预设的目标,那么我们就来理解下什么是最优控制和逆最优控制。
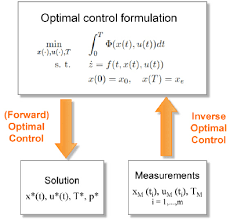
因此,最优控制是期望最小化或者最大化目标。
很显然最优控制和逆最优控制是一种相反的关系:
最优控制理论是数学优化的一个分支,它处理在一段时间内为一个动态系统找到一个控制,使目标函数得到优化。目标是找到目标控制律,使得优化目标函数。
而逆最优控制作为将生物运动传递给机器人的有前途的方法。逆最优控制有助于(a)理解和识别基于测量的生物运动的潜在最优标准,以及(b)建立可用于控制机器人运动的最优控制模型。
逆最优控制问题的目的是确定——对于给定的动态过程和观察到的解——产生解的优化准则。从数学的角度来看,逆最优控制问题是困难的,因为它们需要解决最优控制问题中的参数识别问题。
在最优控制中,总的来看,其本质就是让系统以某种最小的代价来让系统运行,当这个代价被定义为二次泛函,且系统是线性的话,那么这个问题就称为线性二次问题,设计的控制器(即问题的解)可以称为LQR(Linear Quadratic Regulator)线性二次调节器。
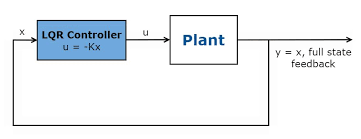
若被动系统是线性化表示,成本函数描述为二次泛函,那么这种问题就可以被认为是线性二次问题,求解此问题,即可以成为LQR问题!
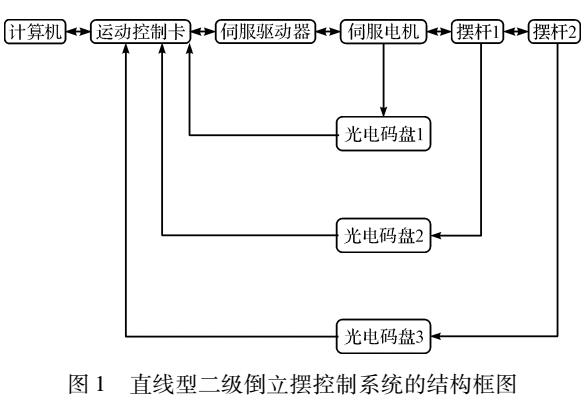
常见的模型为倒立摆模型:
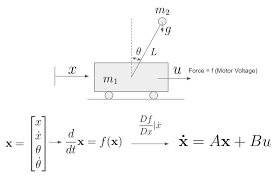
寻找模型的最佳参数的问题被转化为一个 LQR 问题,该问题最大限度地减少了人力并优化了闭环行为。
LQR 控制器的系统具有良好的稳定性,并且在某个性能指标方面是最佳的。然而,当系统高度不确定时,LQR 控制不能保证鲁棒稳定性。
-
控制器
+关注
关注
112文章
16339浏览量
177860 -
机器人
+关注
关注
211文章
28390浏览量
206959 -
调节器
+关注
关注
5文章
847浏览量
46412
发布评论请先 登录
相关推荐
主动队列管理建模及最优控制策略
0038《最优控制理论》科学出版社-2003.pdf(5M)
主动队列管理建模及最优控制策略
大纯滞后对象的最优控制
状态时滞系统的输入多采样最优控制
最优控制在直流调速系统中的应用
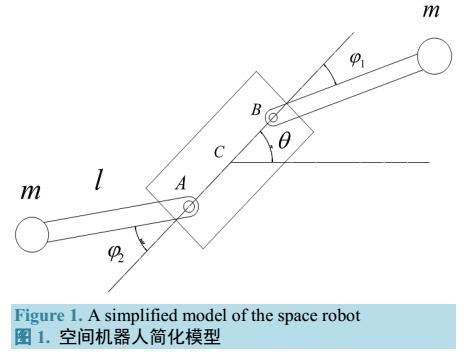
基于Legendre伪谱法的空间机器人姿态运动的最优控制
直线二级倒立摆系统的H∞鲁棒最优控制




 什么是机器人最优控制和逆最优控制
什么是机器人最优控制和逆最优控制
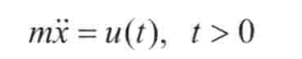










评论