电流源的串联—支路电流分析法案例

在电路中，任何支路上流过的电流都只能是单值的。针对图1中a点的情况可以发现，流出该点的电流比流入的电流大，实际上这是不可能的。因此，不同量值的电流源是不能串联连接的，就像不同量值的电压源不能并联一样。

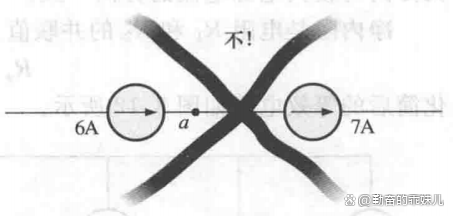
图1

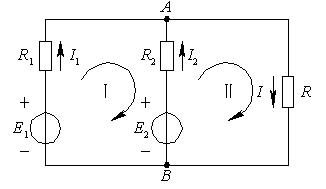
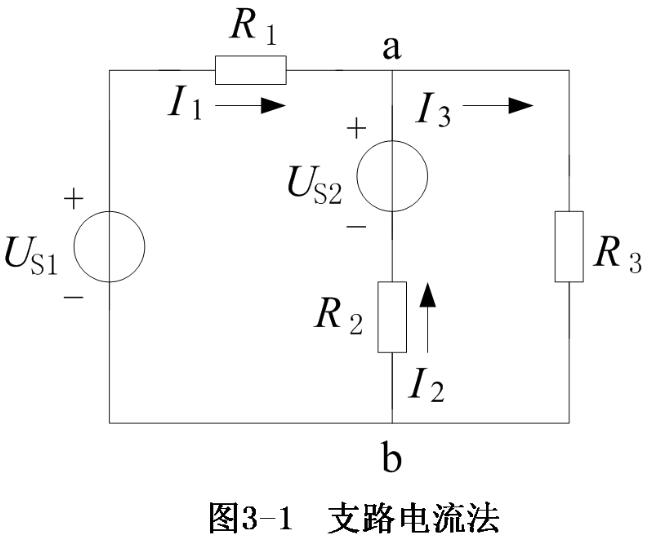
在详细讨论第一个重要的分析方法之前，让我们一起来分析图2中的电路，从而更好地理解为什么需要这些特殊的方法来分析电路。

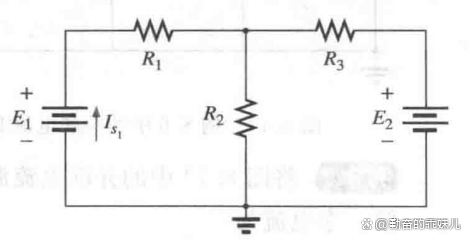
图2

初看上去，我们可以使用化简和反推法向电源E1方向化简，并计算出电源电流Is~~1 。然而串联元件R3和E2是不同类型的元件，所以不能合并。进一步观察可以发现，这个电路没有两个同类元件是串联或并联的。因此不能对元件进行合并，这就明显指出，必须使用另外的方法来求解这个电路。

必须指出，如果我们将每个电压源转换为电流源，然后合并它们，那么就可以求解出图2所示的电路。然而，如果要求解原电路中的某个具体的值，那么就需要利用从电源变换中求得的量往回计算出待求的量。

本次介绍的方法称为支路电流法或支路分析法，这是因为我们将要定义和求解电路中每条支路的电流。介绍这个方法并让大家理解它的应用的最好办法就是总结出一系列的步骤，每个步骤都是精心给出的。下面例子的求解就遵循了这些步骤。

支路电流法分析步骤

1)给电路中的每条支路都标上一个电流，电流的方向任意。

2)根据假定的电流方向，标出每个电阻电压的极性。

3)对电路中每个独立的闭合回路应用基尔霍夫电压定律。

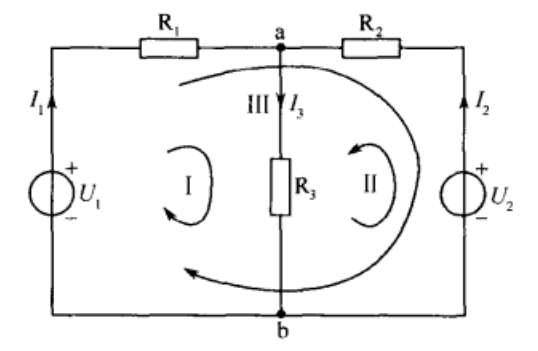
确定需要应用多少次基尔霍夫电压定律的最好方法就是先确定电路中“窗口”(或网孔)的数量。例1中的电路和图2a的结构非常相似，都是两窗口。结果就需要应用基尔霍夫电压定律两次。对于有三个窗的电路，如图2b，则需要应用基尔霍夫电压定律三次，依此类推。

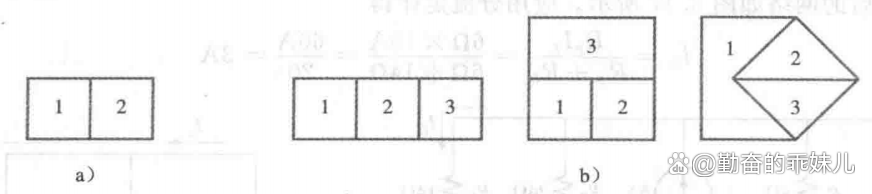
图2

4)在最少个数的节点处应用基尔霍夫电流定律，并且包含网络的所有支路电流。

最少个数就是电路中总节点的个数减1。为了进行说明，规定一个节点就是两个或多个支路的交叉点，其中的支路可以是任意串联元件的组合。图3中给出了图2的每个结构需要应用基尔霍夫电流定律的次数。

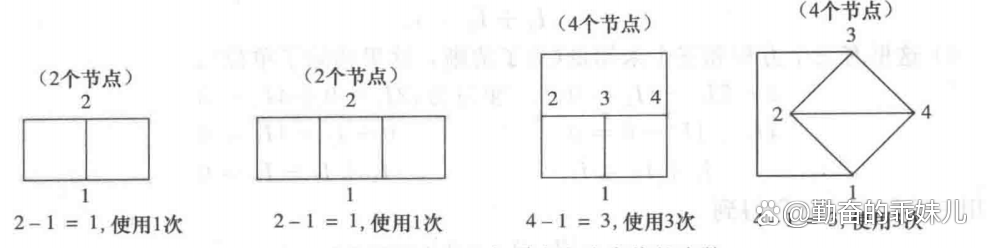
图3

5)根据得到的联立线性方程组，求解假定的支路电流。

假定求解电流I1、I2和I3时使用的行列式方法大家都能理解，并且在数学课中已经学习了这部分内容。使用计算器和计算机软件包，例如MATLAB和Mathcad，可以快速准确地计算出结果。

例1.利用支路电流法求解图4中的电路。

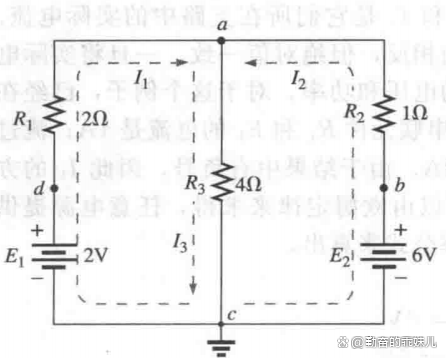
图4

解.

1)由于有三个不同的支路(cda，cba，ca),因此选择了三个任意方向的电流(I 1 、I 2 ，I 3 )，如图4所示。选择电流I1和I2的方向，使其分别与电源E1和E2的电动势方向相同。由于I1和I2都流入节点a，因此将I3标注为流出节点。

2)画出每个电阻上电压的极性，使其与假定的电流方向一致，如图5所示。

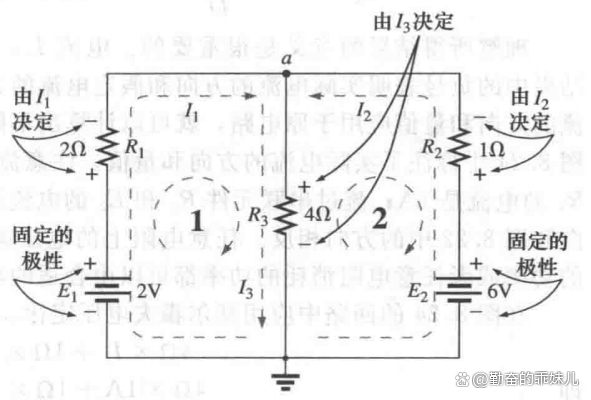
图5

4)在节点a应用基尔霍夫电流定律(在两节点电路中，只需在其中一个节点处应用这个定律)得

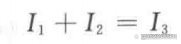
5)这里有三个方程和三个未知量(为了清晰，这里移除了单位):

使用三阶行列式我们得到

负号只是表示实际电流的方向和假定电流的方向相反。

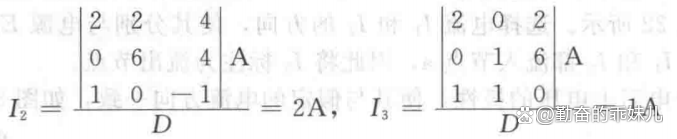
理解所得结果的意义是很重要的。电流I 1， I2和I3 是它们所在支路中的实际电流。结果中的负号表明实际电流的方向和假定电流的方向相反，但绝对值一致。一旦将实际电流的方向和量值应用于原电路，就可以计算出不同的电压和功率。

对于这个例子，已经在图6中标注了实际电流的方向和量值。注意流过串联元件R1和E1的电流是1A；流过R3的电流是1A；流过串联元件R2和E2的电流是2A。由于结果中有负号，因此I1的方向和图4中的方向相反。任意电阻上的电压都可以由欧姆定律来求得，任意电源提供的功率或者任意电阻消耗的功率都可以由合适的功率公式来算出。

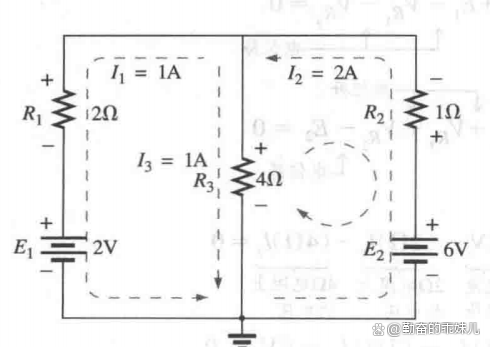
图6

在图6的回路中应用基尔霍夫电压定律，得

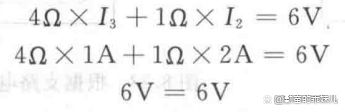
这就验证了结果的正确性。