关于贝叶斯概念进行形式化的建模和推理

来源 | 《趣学贝叶斯统计：橡皮鸭、乐高和星球大战中的统计学》 作者 | [美] 威尔·库尔特（Will Kurt） 译者 |王凌云

本章将概述贝叶斯推理。所谓贝叶斯推理，是指我们在观察到一些数据后，更新自己对这个世界的信念的过程。我们将通过一个场景来探讨如何将日常经验映射到贝叶斯推理中。

好消息是，在拿起本书之前，你就已经是一个贝叶斯主义者了！贝叶斯统计其实与人们如何自然地利用数据创造新的信念、如何进行日常问题的推理密切相关。坏消息是，将这种自然的思维过程分解为严谨的数学过程很难。

在统计学中，我们通过使用特定的计算和模型来更准确地量化概率。不过，本章不会使用任何数学计算或模型，我们只需要熟悉基本概念，并利用直觉来确定概率。我们才会精确地计算概率。在本书的剩余部分，你将学习如何使用严格的数学方法对本章涉及的概念进行形式化的建模和推理。

1 对奇怪经历的推理

一天晚上，你突然被窗外的一道亮光惊醒。你从床上跳起来，向外望去，发现天空中有一个碟形的庞然大物。你从来都不相信会遇见外星人，但现在你完全被外面的景象迷惑了。你发现自己在想：这难道是不明飞行物（unidentified flying object，UFO）吗？！

贝叶斯推理就是这样一种思维过程：在遇到一种情况时，你会做出概率假设，然后根据这些假设更新你对这个世界的信念。在UFO这个情景中，你已经经历了一个完整的贝叶斯分析过程，因为你：

(1) 观察到了数据；

(2) 做出了一个假设；

(3) 根据观察到的数据更新了自己的信念。

这种推理往往发生得太快，以至于你没有时间分析自己的思维过程。你在没有任何质疑的情况下建立了一个新的信念：之前你不相信UFO的存在，在事件发生之后你更新了自己的信念，你认为自己看到了UFO。

本章主要关注信念的产生及其构建过程，这样你就可以更规范地研究它。此外，后面的章节还将研究如何量化这个过程。

让我们从观察数据开始，依次分析这个推理过程的每一个步骤。

（1）观察数据

将信念建立在数据上，是贝叶斯推理的一个关键组成部分。在对场景得出任何结论之前（比如说你声称自己看到了UFO），你需要理解所观察到的数据。在这个例子中，数据是：

窗外的一道亮光；

一个碟形物体在空中盘旋。

根据经验，你会把窗外的景象描述为“令人惊讶的场景”，用概率的术语表示，可以将它写为：

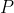(窗外出现亮光, 天空中有碟形物体)  很小

其中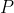 表示概率，括号内列出的是两条数据。你可以将这个等式理解为“窗外出现亮光且天空中有碟形物体的概率很小”。在概率论中，当要表示多个事件的联合概率（combined probability）时，用逗号分隔事件。请注意，这两条数据并不包含任何关于UFO的具体内容，它只由你的观察结果组成——这一点在后面会很重要。

也可以考查单个事件的概率，并将其写为：

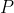(下雨)  很可能

这个等式的意思是，“下雨的概率比较大”。

对刚才提到的UFO场景，我们要确定的是两个事件一起发生的概率。这与两个事件单独发生的概率完全不同。例如，单独出现亮光很容易，一辆路过的汽车就会发出亮光，所以就出现亮光这个事件而言，它发生的概率要远远大于它和碟形物体同时出现的概率（不过碟形物体单独出现也同样让人惊讶）。

如何确定这个概率呢？现在，我们使用的是直觉，也就是自我感觉到的这件事发生的可能性。第2章将介绍如何得出概率的精确数值。

（2）先验信念和条件概率

早晨醒来，煮杯咖啡喝，然后开车去上班。在这个过程中，你不需要做很多分析，这是因为你对这个世界如何运转有着先验信念（prior belief）。先验信念是我们根据一生的经验（也就是观察到的数据）建立起来的信念集合。你相信太阳会升起，因为自你出生以来太阳每天都会升起（当然，在阴雨天，你看不见太阳升起）。如果没有先验信念，我们每天晚上睡觉时都会害怕明天的太阳可能不会升起。

先验信念表示，在看到窗外有明亮灯光的同时看到一个碟形物体，这在地球上很少见。但如果你生活在一个遥远的星球上，那里有大量的飞碟且经常有星际访客，那么在天空中同时看到亮光和碟形物体的概率就会大很多。

在公式中，先验信念写在数据后面并用“|”与数据隔开，就像下面这样：

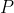(窗外出现亮光，天空中有碟形物体 | 地球上的经验)  很小

这个等式可以理解为：“根据我们在地球上的经验，在天空中同时看到亮光和碟形物体的概率很小。”

这个概率结果被称为条件概率（conditional probability），因为计算某一个事件发生的概率时，以另一个事件的存在为条件。在这种情况下，我们会根据经验来调整观察到的事件的概率。

正如用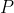 表示概率一样，我们通常用另外的变量来表示事件和条件，这样更简洁。如果你不太熟悉等式，一开始可能觉得它们显得过于简洁。但过一段时间你就会发现，简洁的变量名既有助于提高可读性，也有助于你了解等式如何推广到更大的问题类别上。我们将把所有的数据赋给一个变量 ：

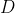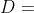 窗外出现亮光，天空中有碟形物体

所以从现在开始，当提到这组数据集的概率时，我们会直接用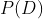 来表示。

同样，我们会用变量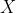 来表示先验信念，像下面这样：

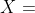 地球上的经验

现在可以将上文中等式的左边写为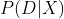。这样写更为简单且意思保持不变。

以多重信念为条件

如果有一个以上的变量会显著影响概率，那么我们可以添加一个以上的先验信念。假设今天是特定节日，根据经验，你知道在这天放烟花很常见。根据你在地球上的经验和今天是特殊的日子，在天空中看到亮光的概率不是完全没有，甚至那个碟形物体也可能与某个烟花表演有关。因此，你可以将这个等式改写为：

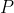(窗外出现亮光, 天空中有碟形物体 | 特定节日, 地球上的经验)  小

对比这两种情况可以发现，条件概率从“很小”变成了“小”。

在实践中假设存在先验信念

在统计学中，通常不会明确地为所有的现有经验附加条件，因为它是可以假设的。出于这个原因，在本书中，我们不会在这种情况下单独增加变量。然而在贝叶斯分析中，我们必须记住，我们对这个世界的理解总是以自己在这个世界上的经验为条件的。本章的其余部分会保留“地球上的经验”这个变量以提醒这一点。

（3）形成假设

到目前为止，我们已经有了数据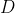（看到了一道亮光和一个碟形物体）和先验信念 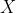。为了解释所看到的情况，我们需要形成某种假设（hypothesis），即形成一个关于世界如何运作的模型，从而做出预测。假设可以有多种形式，我们对这个世界的所有基本信念都可以是假设。

如果相信地球自转，那么你就可以预测太阳会在某个时间升起和落下。

如果认为你最喜欢的棒球队是最好的，那么你就可以预测他们会比其他球队赢得更多。

假设也可以更正式、更复杂。

科学家可能会假设某种治疗方法能减缓癌症恶化。

金融领域的定量分析师会构建市场行为模型。

深度神经网络可以预测哪些图像展示的是动物，哪些图像展示的是植物。

所有这些例子都是假设，因为它们都包含对这个世界的某种理解，并利用这种理解来预测世界将如何运作。当提到贝叶斯统计中的假设时，通常关注的是它对我们观察到的数据的预测能力。

当看到数据并认为自己看到了UFO时，你就在形成一个假设。UFO的假设很可能是基于你以前看过的电影和电视节目。将第一个假设定义为：

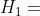 在我家的后院里有一个UFO！

但这个假设预测的又是什么呢？如果将问题倒过来想，我们可能会问：“如果在你家的后院里有一个UFO，那么你预期会看到什么呢？”你可能会回答：“亮光和碟形物体。”因为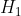 预测了数据 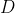，所以当我们在给定的假设下观察到数据时，数据的概率就会增加。这样的结果可以规范地表示为：

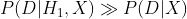
这个式子的意思是：“如果相信这是UFO并根据经验，在天空中看到亮光和碟形物体的概率要远远大于只看到亮光和碟形物体而无法解释的概率（这里用两个大于号 表示远远大于）。”这里用概率的语言证明了我们的假设可以解释数据。

（4）在日常语言中发现假设

很容易看出，日常语言和概率之间有着某种关系。例如，说某事“令人惊讶”，其实就等于说，根据我们的经验，它发生的概率比较小；而说某件事“很合理”，其实是说，基于经验，它发生的概率比较大。一旦指出，这种关系似乎就变得很明显了，但概率推理的关键在于仔细思考如何解释数据、形成假设并改变你自己的信念，即使面对的是一个普通的日常场景。如果没有假设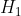，那么你就会感到疑惑，因为你无法解释所观察到的数据。

2 收集更多的数据以更新信念

现在你有了数据和假设，然而由于之前你一直对UFO事件持怀疑态度，因此这个假设看起来还是很离谱。为了进一步提高知识水平以得出更可靠的结论，你需要收集更多的数据。这是统计推理的下一个步骤，也是直觉思维的下一个步骤。

为了收集更多的数据，需要进行更多的观察。具体到UFO这个场景，你需要向窗外看看还能观察到什么。

当去看外面的亮光时，你注意到这个区域还有更多的灯光，还看到那个巨大的碟形物体用电线吊着，并留意到一个摄像人员。你听到一声巨响，有人喊了一声“停”。

你很有可能会瞬间改变对这个场景中所发生事情的看法。之前，你的推断是自己可能看到了一个UFO，现在有了一些新数据，你意识到这看起来更像是有人在附近拍电影。

在这一思维过程中，你的大脑又一次瞬间完成了一次复杂的贝叶斯分析！为了更仔细地分析这一事件，下面来分解这一思维过程。

最初，你的假设是：

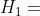 有UFO着陆！

根据你的经验，这个假设单独发生的可能性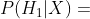非常小：

 非常小

这是在现有数据下，你能想到的唯一可能的解释。但是，当观察到更多的数据后，你立刻意识到还有一个可能的假设——附近有人正在拍摄电影：

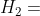 有人正在窗外拍摄电影

这个假设单独发生的概率从直觉上来说也很小（除非你碰巧住在电影制片厂附近）：

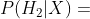 很小

请注意，这里将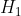 的概率设为“非常小”，并将  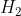的概率设为“很小”。这与我们的直觉相符。假设在没有任何数据的情况下有人走过来询问：“你认为哪一种可能性更大——是UFO夜间出现在你家附近，还是刚好有电影在你家附近拍摄？”你会回答拍摄电影的可能性要比出现UFO的可能性更大。

当改变信念时，我们需要用一种方法将新得到的数据考虑进去。

3 对比假设

最开始，尽管不太相信，但你接受了出现UFO的假设，因为除此之外你想不出任何其他解释。然而现在出现了另一种可能的解释——正在拍摄电影，由此产生了备择假设（alternative hypothesis）。思考备择假设的过程，就是利用你所掌握的数据对多种假设进行比较的过程。

当看到电线、电影摄制组和额外的灯光时，你所掌握的数据就发生了变化。更新后的数据是：

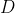更新后  亮光, 碟形物体, 电线, 摄制组, 其他灯光等

在观察到这些额外的数据后，你改变了对所发生事情的结论。下面将这个过程分解成贝叶斯推理过程。第一种假设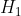 给了一种解释数据的方法，让你不再困惑；然而随着观察的进一步深入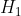， 已经不能很恰当地解释数据了。用概率的方法表示就是：

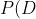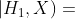更新后  非常小

现在你有了一种新的假设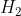，它可以更恰当地解释数据，用概率的方法表示就是：

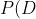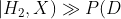更新后 更新后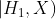 

这里的关键是，要理解我们是在比较这些假设对观测数据的解释程度。当说“在第二种假设中，数据的出现概率要远远大于第一种假设”时，我们的意思是，第二种假设可以更恰当地解释所观察到的数据。由此，我们就触及了贝叶斯分析的真正核心：检验信念的标准是它们解释世界的能力。我们说一种信念要比另一种信念更准确，是因为它能更恰当地解释我们所观察到的世界。

数学上用这两种概率的比值来表达这个想法：

当这个比值是一个很大的数时，比如1000，它意味着“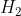 对数据的解释要比  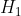恰当1000倍”。因为  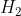对数据的解释要比  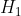好很多，所以我们将信念从  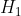改变为 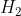。这正是当你改变对所观察情况的看法时所发生的事情。现在你之所以相信自己看到的是窗外正在拍摄电影，是因为它更能解释你所观察到的所有数据。

4 数据影响信念，信念不应该影响数据

最后值得强调的一点是，所有这些示例中唯一不变的是数据。你的假设可以改变，你在这个世界上的经验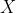 也可以与别人不同，但是数据  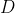则是所有人共享的。

思考下面这两个公式。第一个已经在本章中多次使用：

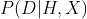
它可以理解为“根据给定的假设和我的经验所得出的数据概率”，或者更直白地说，“我的信念对所观察到的数据解释得如何”。

但在日常思维中，有一种反过来的情况，那就是：

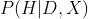
它可以理解为“根据数据和在这个世界上的经验，我的信念的概率”，或者“我观察到的情况对我的信念的支持程度”。

在第一种情况下，我们会根据所收集到的数据和对世界的观察来改变自己的信念，从而更恰当地描述这个世界。在第二种情况下，我们收集数据来支持自己当前的信念。贝叶斯思维就是改变你的想法，更新你对世界的理解。我们观察到的数据都是真实的，所以我们的信念终归需要转变，直到与数据一致。

在生活中，你的信念也应该是始终可变的。

当摄制组收工时，你注意到所有的面包车上都有同一个徽章图案。你隐约听到有人说：“嗯，这应该骗过了所有看到这一场景的人……真是好主意。”

有了这些新数据后，你的信念可能会再次改变！

5 小结

下面来回顾一下本章所介绍的内容。你根据现有的经验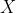 形成了最初的信念。而观察到的数据 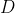，要么与你的经验一致，即  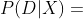很大；要么让你感到惊讶，即  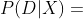很小。为了理解这个世界，你信赖根据观察所形成的信念，或者说假设 。很多时候，一种新的假设可以解释让你感到惊讶的数据，用概率的语言表示就是 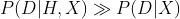。当收集到新的数据或产生新的想法时，你可以形成更多的假设，如 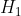、、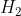 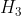等。当一种新的假设要比旧的假设更能解释收集到的数据时，即当出现下面这种情况时，你会改变自己的信念。

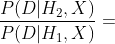 较大数值

最后，你应该更关注那些改变你的信念的数据，而不是确保数据支持你的信念，即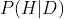 的值。

有了这些基础，就可以往其中添加数值了。你将用数学方法interwetten与威廉的赔率体系 自己的信念，从而精确地决定你应该如何以及何时改变自己的信念。

6 练习

试着回答以下问题，检验一下你对贝叶斯推理的理解程度。

(1) 使用本章介绍的数学符号，将下列表述改写为数学表达式：

下雨的概率较小；

在阴天，下雨的概率较大；

下雨时，你带伞的概率要远远大于通常情况下带伞的概率。

(2) 使用本章介绍的方法，将你在下述场景中观察到的数据整理为数学表达式，然后提出假设来解释这些数据。

你下班回到家，看到正门是开着的且侧窗坏了。走进门后，你很快发现自己的笔记本计算机不见了。

(3) 下述场景在第2题的基础上增加了一些数据。使用本章介绍的数学符号演示这些新信息如何改变你的信念，并提出第2个假设来解释这些数据。

邻居家的孩子跑过来向你道歉，他不小心将石头扔到你家的窗户上，打碎了玻璃。同时他还说，他看见了你的笔记本计算机，因为不想让它被偷，所以他打开正门将它拿回了家。现在你的笔记本计算机在他家，很安全。

编辑：黄飞