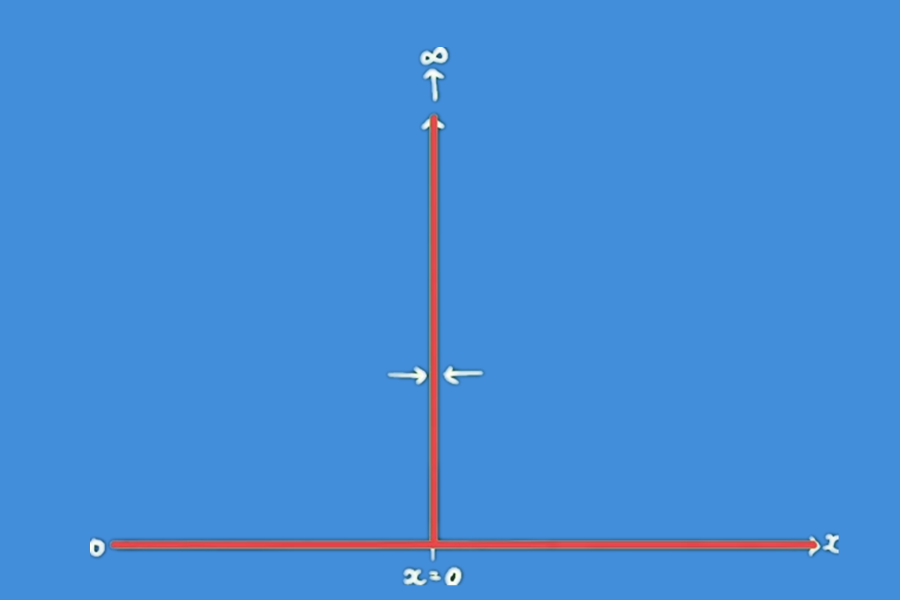
在这篇文章中,我想谈一个在物理研究中非常重要的想法,它实际上是一个数学函数,称为狄拉克δ函数。在x等于0时,δ函数的值非常大,它是无限大。而在x不等于0的其他地方,δ函数的值恒等于0。换句话说,δ函数是一个无限薄且无限大的尖峰。在我们讨论δ函数在物理学中的用途之前,我们要先看看δ函数的一些数学特性。
回想一下,对于一般函数,我们是如何求解它的函数图像与x轴之间的面积的?大多数函数不是由简单的形状组成的,但我们可以想象将这个区域分成许多小块,通过将其视为矩形或梯形来找到每个小块的面积,然后将它们全部相加得到总的面积,这就是我们对函数进行积分的意思。
考虑到x等于0时,δ函数的宽度为零,它的下方没有任何面积。但它的高度是无限的,所以我们给了它一个定义,这个函数下的面积最终是有限的,它的面积为1。
δ函数实际上不需要专门在x等于0时处于尖峰,我们实际上可以将尖峰移动到不同的位置。如果我们取因变量x,然后从中减去一些量(假设是 a),则δ(x-a)的函数图像将移动相同的量a,然后这个函数在x等于a就处于峰值。
这个性质很要的原因是,我们现在可以采用另一个函数,比如说正弦函数sin(x),然后将它与δ(x-a)想成,最后再对其进行积分,那么我们最终得到的是函数的值sin(a):。换句话说,当以这种方式使用δ函数时,可以用来挑选任何函数的特定值。
关于δ函数的数学属性已经足够了,那么它在物理学中是如何被使用的?尽管这些无穷大并没有真正出现在现实生活中,但理论物理学中却充满了它们的身影。例如,为了简单起见,我们经常将粒子视为一个点。这意味着,我们假设像电子这样的小粒子的质量,集中在粒子正中心的一个点上,这个点被称为质心。
以类似的方式,我们说该电荷集中在一个非常小的点上。事实上,无限小是为了使我们所有的计算变得更容易,而不是必须处理分布在一个小但有限的空间上的电荷。所以在这里,我们就可以使用δ函数对这样的想法进行数学编码。
首先,我们考虑的不是粒子的电荷q,而应该是电荷密度ρ。电荷密度是我们在每单位体积中找到的电荷量ρ=q/v,用更正确的方式来说,它实际上是电荷变化dq相对于体积dv的变化率:ρ=dq/dv。现在,我们可以通过这个逆过程,来找到粒子的电荷:q=∫ρdv。
对此的物理解释是,粒子的电荷可以通过找出空间区域中每个微小体积有多少电荷来给出。我们将电荷密度乘以每个微小体积,得到在此体积中的电荷,然后我们将所有这些电荷相加得到总电荷:q=dq₁+dq₂+……
但请记住,对于一个简单的粒子,我们假设电荷实际上根本没有分布,而是全部在一个点上找到,所以电荷密度用上述所说的定义是不太方便的。事实上,我们可以用δ函数来定义,比如在x=a处:ρ=qδ(x-a)。为什么要这样做呢,让我们将其代回积分方程看看会发生什么。
前面我们已经介绍过δ函数的属性,在这种情况下积分时,δ函数会选出与其相乘的函数的值,所以q=∫ρdv=∫qδ(x-a)dv=q(a)。从数学上讲,我们只是用δ函数对q进行编码。但从物理上来讲,δ函数可以帮助我们在带电粒子实际所在的空间点上找出它。
总结一下,当我们处理带电粒子时,它们与我们通常习惯的尺度相比是如此之小。当我们必须进行详细的计算时,我们假设粒子可能无限小并且仅定位于空间中的一个点。在大多数情况下,我们直接使用δ函数是非常合适的,它会使得事情变得更简单。
δ函数在物理学中还有很多应用,举一个生活中比较常见的例子。踢足球的时候,我们的脚在会在短时间内对物体进行作用。这时候,我们就可以使用δ函数。只不过,这次不像粒子那样在空间中定位电荷,而是在时间上定位某个属性。
-
函数
+关注
关注
3文章
4331浏览量
62604 -
函数图像
+关注
关注
0文章
2浏览量
1530
原文标题:理论物理学中的一个重要数学函数
文章出处:【微信号:bdtdsj,微信公众号:中科院半导体所】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
2024年诺贝尔物理学奖为何要颁给机器学习?
超导现象的应用与影响 超导体在量子计算中的作用
无所不能的MATLAB|证明曲速引擎的物理学原理

光电效应在半导体中的应用
光电效应与电子伏特效应的区别
机械振动的三个基本要素
神经网络中的激活函数有哪些
傅里叶变换的应用 傅里叶变换的性质公式
量子半导体实现拓扑趋肤效应可用于制造微型高精度传感器和放大器
差示扫描量热仪 紫薯抗性淀粉的制备工艺及物理学特性研究





 理论物理学中的一个重要数学函数
理论物理学中的一个重要数学函数














评论