怎么增加差分对的线性范围?
差分算法是一种常用的计算机算法,用于解决序列上的差的问题。差分对的线性范围是指一段序列中存在的差分对的数量的线性增长范围。在本文中,我们将探讨如何增加差分对的线性范围。
差分算法的基本原理是将一个序列中的相邻元素的差值存储在另一个数组中。这个数组称为差分数组,它的长度比原序列少1。通过这种方法,我们可以在O(1)的时间复杂度内对序列进行更改操作,而不必重新计算整个序列的值。
差分算法的应用非常广泛,它可以用于解决排序问题、数组区间修改问题、连通性问题等。其中,最常见的应用场景是数组区间修改问题。例如,给定一个长度为n的数组A和一个包含m个修改操作的序列,每个操作包含一个左端点l和右端点r以及一个修正值v。我们需要对数组A进行m次修改操作后,计算A中任意一段区间的和。
假设我们有一个差分数组D,它的第i个元素是A[i]-A[i-1],即原数组的相邻元素之差。那么,区间[l,r]的和就可以通过下面的公式计算得出:
sum[l,r] = A[l] + D[l+1] + D[l+2] + ... + D[r]
通过这种方法,我们只需要修改差分数组D就可以对原数组进行区间修改操作,并且时间复杂度是O(1)。
现在我们来考虑如何增加差分对的线性范围。首先,我们需要了解差分对的定义。一个差分对是指数组D中相邻元素之差为正数的一对位置。例如,对于差分数组D=[1, 2, -3, -1, 4],它包含两个差分对(1,2)和(4,5)。
增加差分对的线性范围的方法有很多种,下面我们将介绍其中的两种方法。
方法一:增加原序列中的冗余元素
要增加差分对的线性范围,我们可以将原序列中的冗余元素添加到末尾。例如,假设原序列为A=[3, 1, 4, 6, 7],我们可以将它扩展为A'=[3, 1, 4, 6, 7, 0, 0, 0, ...],然后对它进行差分运算得到差分数组D=[3, -2, 3, 2, -7, 0, 0, 0, ...]。这个差分数组包含了更多的正数和负数,因此它的线性范围更大。
由于我们需要将冗余元素添加到末尾,因此这种方法的时间复杂度是O(n)。实现时需要注意,扩展后的数组长度必须是2的幂次方,可以通过在数组末尾添加一些值为0的元素来实现这一点。
方法二:应用四边形不等式
四边形不等式是一个重要的算法原理,它可以用于优化区间加法操作的时间复杂度。在差分算法中,我们也可以应用这个原理来增加差分对的线性范围。
假设我们需要对原序列进行n次修改操作,并且每个操作的修改值都相同。我们可以将这些操作分为若干个块,每个块包含k个连续的操作。通过计算差分数组D中每个块的偏差,我们可以将序列的修改操作转换为每个块的加法操作。例如,对于原序列A=[3, 1, 4, 6, 7],差分数组D=[3, -2, 3, 2, -7],我们可以将它分为两个块,每个块包含3个操作。第一个块对应的偏差为D[1]+D[2]+D[3]=-2,因此我们可以将它转换为A[2],A[3],A[4]的加法操作,即A[2]+=v,A[3]+=v,A[4]+=v。第二个块对应的偏差为D[4]+D[5]=-7,因此我们可以将它转换为A[5],A[6],A[7]的加法操作,即A[5]+=v,A[6]+=v,A[7]+=v。
通过应用四边形不等式,我们可以将每个块的加法操作转换为两个加法操作,在这个过程中引入一些冗余元素。例如,对于上面的例子,我们可以将第一个块的加法操作转换为A[2]+=v,A[3]+=v,A[4]+=v,A[5]-=v,A[6]-=v,A[7]-=v,这样可以增加两个差分对(2,3)和(5,6)。通过这种方法,我们可以将差分对的线性范围增加到O(n/log n)。
总结
在本文中,我们探讨了如何增加差分对的线性范围。通过增加原序列中的冗余元素和应用四边形不等式,我们可以在不增加时间复杂度的情况下增加差分对的数量。这些方法在实际应用中非常有用,可以帮助我们更快地解决实际问题。
-
差分对
+关注
关注
0文章
9浏览量
6850
发布评论请先 登录
相关推荐
前端的audio codec输出信号为R/L/GND, 如何变成差分对信号输入TPA3113D2?
霍尔效应中uh和im的线性范围
THS4524的差分输入范围是多少?
4芯M8接口的线性范围是多少

LED汽车大灯-线性方案
如何对PCB进行差分对的走线操作呢?
差示扫描量热仪测试范围和工作原理

低压差线性稳压器电路图分享
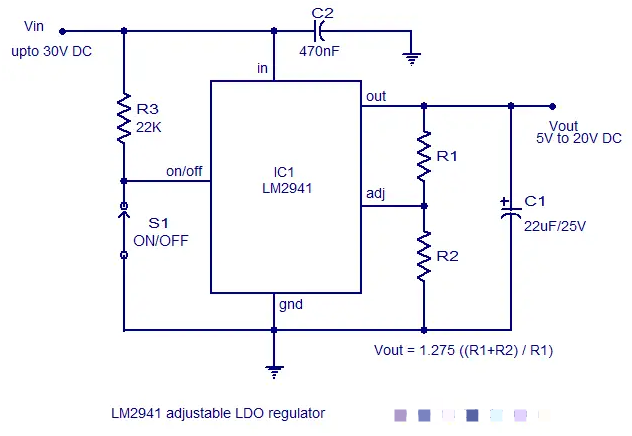
低压差线性稳压器的特点有哪些




 怎么增加差分对的线性范围?
怎么增加差分对的线性范围?












评论