拉普拉斯变换公式
拉普拉斯变换公式是数学中极其重要的一种变换方式,它的应用领域非常广泛,包括在信号处理、控制论、微分方程、电路分析和量子力学等领域中都有着广泛的应用。本文将详细介绍拉普拉斯变换公式的定义、性质、应用和相关计算方法。
定义:
拉普拉斯变换是一种线性变换,它将一个时间域函数 f(t) 转换为一个复平面上的函数 F(s),满足以下公式:
F(s) = L[f(t)] = ∫(0,∞) e^(-st) * f(t) dt
其中 L[f(t)] 表示将函数 f(t) 进行拉普拉斯变换得到的函数 F(s),s 是复平面上的参数,被称为拉普拉斯变量。
性质:
拉普拉斯变换有许多重要的性质,以下是最为重要的几个性质:
1、线性性质:对于任意实数 a 和 b ,有 L[af(t)+bg(t)] = aL[f(t)] + bL[g(t)]
2、平移定理:若 h(t)=f(t-a),则 L[h(t)] = e^(-as) * L[f(t)]
3、尺度定理:若 h(t) = f(at),则 L[h(t)] = (1/a) * F(s/a)
4、卷积定理:L[f(t)*g(t)] = F(s)G(s)
5、初始值定理:lim t→0+ f(t) = lim s→∞ sF(s)
6、终值定理:lim t→∞ f(t) = lim s→0 sF(s)
应用:
拉普拉斯变换在实际应用中有着广泛的应用,以下列举其中几个典型应用:
1、信号处理:在数字信号处理中,拉普拉斯变换可以被用来将信号从时间域转换到频域,由此得到信号的频率特性。
2、微分方程:拉普拉斯变换可以被用来解决各种不同类型的微分方程,例如线性常系数微分方程。
3、控制论:拉普拉斯变换在控制论中被广泛利用,它可以帮助控制系统的设计、分析和优化。
4、电路分析:在电路分析中,拉普拉斯变换可用来表示电路的幅频响应和阶跃响应。
计算方法:
计算复杂的拉普拉斯变换可能需要进行计算技巧的运用,以下列举几种常用的计算方法:
1、部分分式分解:当被转换的函数不符合任何已知运算公式时,可以使用部分分式分解法将其分解成若干个比较简单的函数,这样就可以利用已知的运算公式进行计算。
2、结合卷积定理:当被转换的函数可以表示为两个已知函数的卷积时,可以使用卷积定理将其转换为两个已知函数的拉普拉斯变换相乘的形式,简化计算。
3、利用初始值定理和终值定理:在某些情况下,可以利用初始值定理和终值定理来避免繁琐的积分计算。
结语:
拉普拉斯变换是一种非常强大的数学工具,它可以被用来解决许多应用问题。本文简单介绍了该变换的定义、性质、应用和常用计算方法,希望能对读者有所帮助。在实际应用中,我们需要熟练掌握其基本理论和方法,灵活运用,才能在实际问题中得到应有的解决方案。
-
控制器
+关注
关注
112文章
16339浏览量
177854 -
信号处理器
+关注
关注
1文章
254浏览量
25272 -
拉普拉斯
+关注
关注
0文章
35浏览量
9651
发布评论请先 登录
相关推荐
傅立叶变换与拉普拉斯变换的区别
先进产能设备提供商拉普拉斯科创板上市
拉普拉斯变换的作用及意义
数字信号处理三大变换关系包括什么
如果SPI启动失败,如何创建可通过USB启动的两阶段启动加载程序?
降本增效取得新进展,拉普拉斯申请晶圆图形化工艺专利
CY7C65215A作为从站,在主站写入时响应NAK是怎么回事?
Intersolar 2024丨慕尼黑,拉普拉斯来了!
拉普拉斯IPO:科技与产业深度融合,实现业务领域延展
证监会同意拉普拉斯上交所科创板IPO注册
拉普拉斯科创板IPO过会
傅里叶变换和拉普拉斯变换的关系是什么
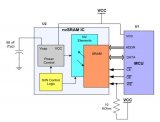
赛普拉斯的NV-SRAM接口解决方案




 拉普拉斯变换公式
拉普拉斯变换公式










评论