介绍
当直流电源电压施加到电容器上时,电容器缓慢充电,最后到达完全充电位置。此时,电容器的充电电压等于电源电压。
在这里,只要施加电压,电容器就充当能量源。电容器在充满电后不允许电流 (i) 通过它们。流过电路的电流取决于电容器极板中的电荷量,并且电流与施加到电路的电压变化率成正比。即 i = dQ/dt = C dV(t)/dt。
如果将交流电源电压施加到电容器电路,则电容器根据电源电压的频率速率连续充电和放电。交流电路中电容器的电容取决于施加在其上的电源电压的频率。在交流电路中,当电源电压相对于时间连续变化时,电容器允许电流。
交流电容器电路
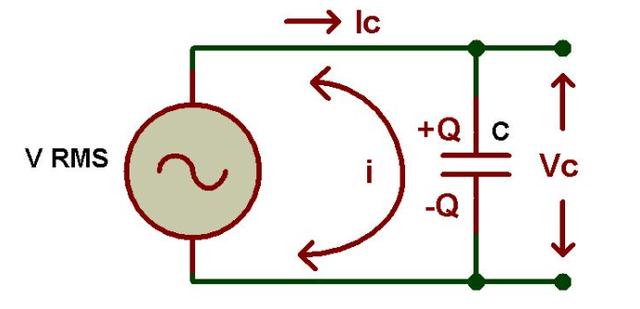
在上面的电路中,我们观察到电容器直接连接到交流电源电压。在这里,电容器根据电源电压的变化不断充电和放电,因为交流电源电压值不断增加和减少。我们都知道,流过电路的电流与施加电压的变化率成正比。
在这里,如果电源电压从正半周期越过其值到负半周期,则充电电流具有高值,反之亦然。即在 00和 1800在正弦波信号中。当正弦波中的电源电压越过其最大或最小峰值(Vm)时,流过电容器的电流具有其最小值。因此,我们可以说流过电路的充电电流是最大或最小,具体取决于正弦波中的电源电压电平。
交流电容相量图

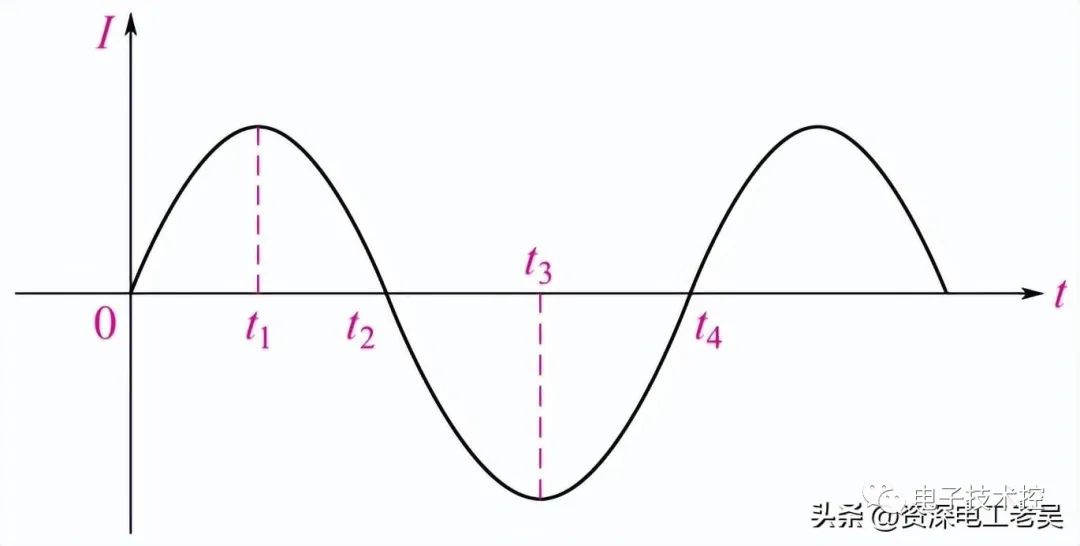
交流电容器的相量图如上图所示,这里的电压和电流以正弦波形式表示。在上图中,我们观察到在 00充电电流处于最大值,因为电压在正方向上缓慢增加。90岁时0没有电流流过电容器,因为此时电源电压处于其最大峰值。
在 1800点电压缓慢降至零,电流在负方向上处于最大值。充电再次达到360的最大值0,因为此时电源电压处于最小值。
从上图中的波形可以看出,电流领先电压900.因此,我们可以说,在理想的电容器电路中,交流电压滞后电流900.
容抗
我们知道,流过电容器的电流与施加电压的变化率成正比,但电容器也提供某种形式的电阻,与电阻器一样。交流电路中电容器的这种电阻称为容抗或通常称为电抗。电容电抗是电容器的特性,它反对交流电路中的电流流动。它用符号Xc表示,并以欧姆为单位测量,与类似电阻相同。
我们需要一些额外的能量来超过容抗来为电路中的电容器充电。该值与电容值和电源电压频率成反比。
Xc∝ 1/c 和 Xc∝ 1/f。
容抗方程和影响它们的参数将在下面讨论。
容抗,
XC = 1/2πfC = 1/ωC
这里
XC = 电容器的电抗
f = 频率(以赫兹为单位)
C = 电容器的电容,单位为法拉
Ω (欧米茄) = 2πf
从上式中我们了解到,当频率和电容值较低时,容抗很高,在此阶段,电容器充当完美的电阻器。如果电源电压的频率高,则电容器的电抗值较低,并且在此阶段电容器充当良导体。从上式可以清楚地看出,如果频率为无穷大,则电抗为零,而当频率为零时,电抗值为无穷大。
容抗频率

上图显示了电源电压的容抗、电流和频率之间的关系。在这里,我们观察到,如果频率低,则电抗很高。充电电流随着频率的增加而增加,因为电压的变化率随着时间的推移而增加。电抗在频率为零时处于无穷大值,反之亦然。
交流电容示例No1
求出流过具有连接到 3V 和 660Hz 电源的 40uF 电容器的电路的电流的均方根值。
XC = 1/2πfC
f = 40HZ
C = 3uF
Vrms = 660V
现在
XC = 1/(2 × 3.14 × 40HZ × 3 × 10-6) = 1326Ω
IRMS = Vrms/XC = 660V/1326Ω = 497mA
交流电容示例No2
求出流过具有连接到 5V 和 880Hz 电源的 50uF 电容器的电路的电流的均方根值。
f = 50HZ
C = 5uF
Vrms = 880V
XC = 1/(2 × 3.14 × 50HZ × 5 × 10-6) = 636Ω
Irms = Vrms/XC = 880V/636Ω = 1.38 A
从上述两个例子中,我们观察到电容器的电抗取决于电源电压的频率,并且呈成反比关系。在示例1中,电抗为1326HZ的频率为40Ω,但当频率增加到636HZ时,电抗值降低到50Ω,如示例2所示。
-
电容器
+关注
关注
64文章
6222浏览量
99626 -
正弦波
+关注
关注
11文章
643浏览量
55398 -
电源电压
+关注
关注
2文章
989浏览量
23984 -
电容充电
+关注
关注
0文章
68浏览量
8600 -
充电电流
+关注
关注
2文章
54浏览量
10494
发布评论请先 登录
相关推荐
交流电路中电容和阻抗之间的关系,如何计算电容器的阻抗?




 交流电路中的电容简析
交流电路中的电容简析











评论