在二维中,我们可以在平面上放置一个网格,然后每个点都用一对数字来表示。
这种结构并不特定于二维,我们还可以添加第三维度。
但是,我们不能再为第四个维度的空间绘制网格了,不过依然可以写下四维向量,它们只是一行四个数字。
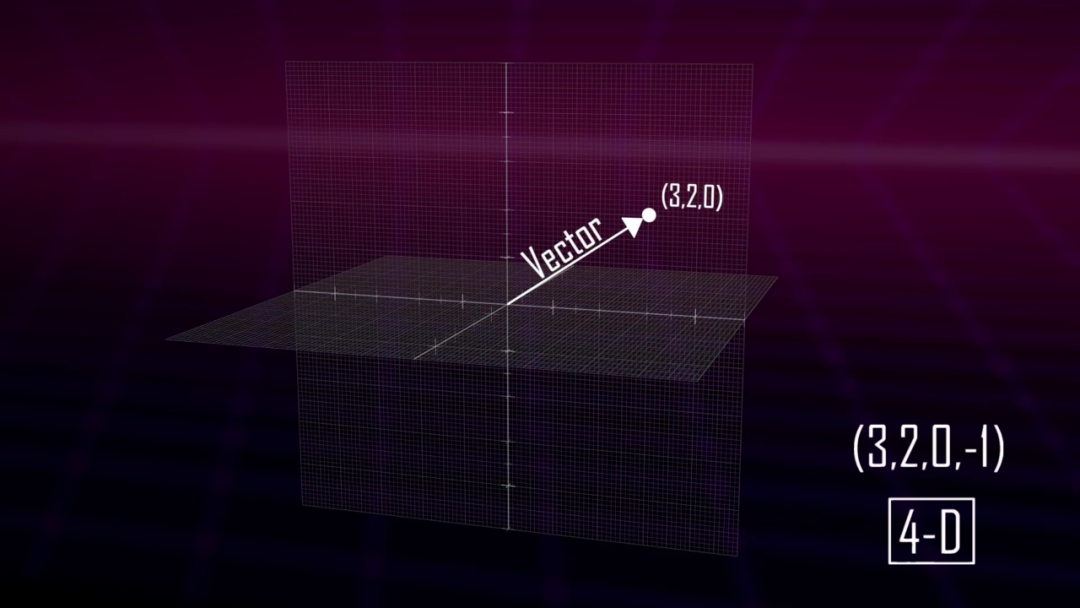
实际上,我们可以构建任何维数的向量。有了更高维度的向量,我们就可以用它们来研究几何学,例如构建更高维度的平面或立方体。
虽然我们不能直接绘制这些高维对象,但我们可以将它们的投影绘制到低维中。
高维几何听起来很天真,但这是朝着数学抽象思维迈出的一大步。
它标志着现在所谓的“纯数学”的开始,即为数学本身而追求的数学,不一定是因为它有应用。
然而,抽象的数学概念往往对物理学有用。
这些高维几何对物理学家来说真的很方便,因为在物理学中,我们通常不仅要处理位于特定位置的事物,还要处理也会沿特定方向移动的事物。
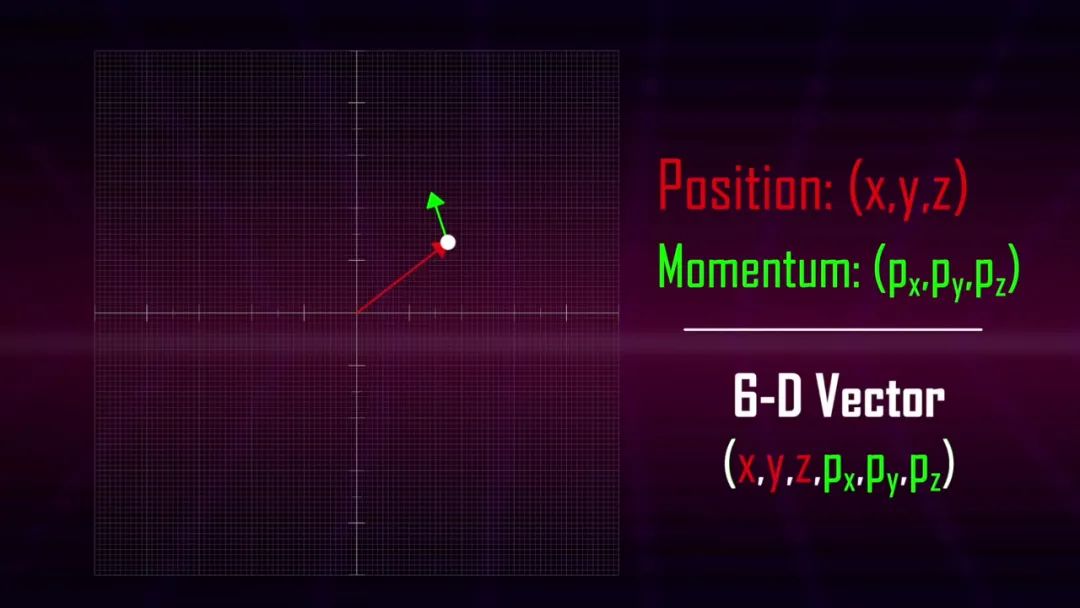
例如,如果我们有一个粒子要描述它的作用,我们分别需要位置和动量的三维信息,因此实际上每个粒子都由一个六维空间中的向量来描述。
这个六维空间称为相空间,通过处理相空间,物理学家变得习惯于处理更高维度的几何形状。
自然而然,他们开始怀疑我们所居住的实际空间是否可以拥有更多的维度。
卡鲁扎-克莱因理论
这个想法最初是由芬兰物理学家贡纳尔·努德斯特伦提出的,他在1914年尝试使用空间的第四维度来描述引力,但没有成功。
弄清楚引力如何工作的是爱因斯坦,他告诉我们引力不需要额外的空间维度。
空间的三个维度就足够了,只是你必须添加一个时间维度,并让所有这些维度都弯曲。
但是,如果你不需要额外的引力维度,那么我们可以将它用于其他用途。
1921年,西奥多·卡鲁扎写了一篇论文,其中他试图使用空间的第四维度来描述电磁力,但却没有解释第四维度在哪里。
几年后,奥斯卡·克莱因解决了这个问题,他认为空间的第四维度必须蜷缩得很小。
这样一来,我们就很难发现它存在,也就符合我们的现实感受。
这种认为电磁力是由空间的第四维卷曲引起的想法现在被称为卡鲁扎-克莱因理论。

这种需要额外维度的想法非常有效,它完全用几何方式解释了力。
可能正因为如此,爱因斯坦晚年才相信几何是物理学基础统一理论的关键。但至少到目前为止,还没有人成功给出大一统理论。
理论缺陷
我们实际上并没有使用卡鲁扎-克莱因理论来替代电磁学,这是因为该理论存在一些严重的问题。
第一个问题是,虽然附加维度的几何形状正确地为我们提供了电场和磁场,但它并没有为我们提供带电粒子,例如电子。
第二个问题是额外维度的半径不稳定,如果我们扰动它,半径可能会开始增加,并产生我们应该看到却没有看到的可观察后果。
第三个问题是理论没有量子化,没有人想出如何量子化几何而不遇到问题。
但是,我们却可以毫无问题地量子化普通电磁学。
当然,我们今天也知道电磁力实际上与弱力相结合成所谓的电弱力。
有趣的是,这种结合对卡鲁扎-克莱因理论来说不是问题。
事实上,在1960年代,物理学家理查德·克纳表明,人们不仅可以用卡鲁扎-克莱因理论做电磁学,还可以为弱力和强力应用卡鲁扎-克莱因理论,我们只需要添加更多维度就行。
对于弱力,我们需要另外两个空间维度。而对于强力,我们需要另外四个空间维度。
所以总的来说,我们现在有1个时间维度,3个引力维度,1个电磁力维度,2个弱力维度,4个强力维度,总共有11个维度。
巧合的是,1981年爱德华·威滕注意到11维恰好也是M理论需要的维数。
审核编辑:刘清
-
处理器
+关注
关注
68文章
19281浏览量
229775 -
向量机
+关注
关注
0文章
166浏览量
20875 -
电磁场
+关注
关注
0文章
791浏览量
47264
原文标题:用几何描绘物理学的统一理论:卡鲁扎-克莱因理论
文章出处:【微信号:bdtdsj,微信公众号:中科院半导体所】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐




 浅析用几何描绘物理学的统一理论
浅析用几何描绘物理学的统一理论










评论