前言
今天在网上看笔试题发现有个设计浮点累加器的题目,看了下题目说明感觉不太清楚,恰好记得之前做过浮点数的加法运算的设计,索性就改了下题目需求,作为一个小练习在重新设计一遍。具体设计要求如下:
设计需求
设计一个32bit浮点的加法器,out = A + B,假设AB均为无符号位,或者换个说法都为正数。
clk为系统时钟;rst_n为系统复位,低有效;en信号控制数据输入;busy指示模块工作状态,busy拉高时,输入无效;aIn和bIn是数据输入,out_vld,指示输出数据有效。
设计的信号列表如下:
module float_adder(
input clk,
input rst_n,
input en,
input [31:0] aIn,
input [31:0] bIn,
output reg busy,
output reg out_vld,
output reg [31:0] out
);
32bit的浮点格式
EE标准754规定了三种浮点数格式:单精度、双精度、扩展精度。前两者正好对应C语言里头的float、double或者FORTRAN里头的real、double精度类型。本文设计实现的为单精度。
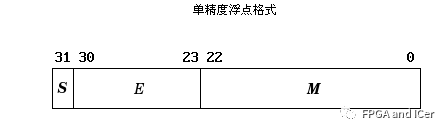 单精度格式
单精度格式单精度:N共32位,其中S占1位,E占8位,M占23位。
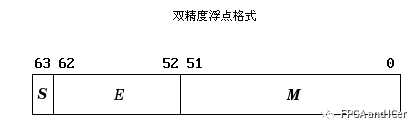 双精度格式
双精度格式双精度:N共64位,其中S占1位,E占11位,M占52位。
浮点数的加法过程
运算过程:对阶、尾数求和、规格化、舍入、溢出判断
对阶:
和定点数不相同的是,浮点数的指数量级不一定是一样的,所以这也就意味着,尾数直接进行加法运算时会存在问题,也就需要首先对阶数进行处理。该过程有点像科学计数法的加法处理,把科学计数法的指数化为一致,求出来指数相差多少,然后移位处理后再进行加法减法。所以这里处理也要先求阶差。
如果把阶码大的向阶码小的看齐,就要把阶码大的数的尾数部分左移,阶码减小。这个操作有可能在移位过程中把尾数的高位部分移掉,这样就引发了数据的错误,所以,尾数左移在计算机运算中不可取。
如果把阶码小的向阶码大的看齐,在移位过程中如果发生数据丢失,也是最右边的数据位发生丢失,最右边的数据位丢失,只会影响数据的精度,不会影响数据的大小。
尾数求和:
这里就是常规的补码加法。
规格化:
右规(尾数的绝对值太大时,右规)尾数右移一位,阶码加1。当尾数溢出( >1 )时,需要右规。是否溢出,可以通过两位的符号位得出:即尾数出现01.xx…xx或10.xx…xx(两位符号位不同)
提高浮点数的表示精度,这里设计考虑比较简单,我只考虑了同号数据相加的情况,所以这里只设计了右规的情况,不考虑符号位。
舍入判断:
这里直接用截断处理的方式,针对数据相加上溢的情况,规定了运算后上溢后将数据规定为最大值。
实现代码
module float_adder(
input clk,
input rst_n,
input en,
input [31:0] aIn,
input [31:0] bIn,
output reg busy,
output reg out_vld,
output reg [31:0] out
);
//运算过程:对阶、尾数求和、规格化、舍入、溢出判断
//分离阶数、尾数
wire signal_bit = aIn[31];
wire [7:0] pow_a = aIn[30:23];
wire [7:0] pow_b = bIn[30:23];
wire [22:0] val_a = aIn[22:0];
wire [22:0] val_b = bIn[22:0];
//找到输入指数阶数较大,和阶数差
//对阶:在计算机中,采用小阶向大阶看齐的方法,实现对阶。即右移
reg [22:0] pow_max ;
reg [23:0] pow_dif ;
reg [22:0] val_max ;
reg [22:0] val_min ;
reg en_dly0;
always @(posedge clk or negedge rst_n) begin
if(rst_n==0)begin
pow_max <= 'd0;
val_max <= 'd0;
val_min <= 'd0;
pow_dif <= 'd0;
en_dly0 <= 'd0;
end
else if( en == 1 && busy == 0)begin
if(pow_a >= pow_b)begin
pow_max <= pow_a;
val_max <= val_a;
val_min <= val_b;
en_dly0 <= 'd1;
if ( pow_a - pow_b > 'd23) begin
pow_dif <= 'd23;
end
else begin
pow_dif <= pow_a - pow_b;
end
end
else begin
pow_max <= pow_b;
val_max <= val_b;
val_min <= val_a;
en_dly0 <= 'd1;
if ( pow_b - pow_a > 'd23) begin
pow_dif <= 'd23;
end
else begin
pow_dif <= pow_b - pow_a;
end
end
end
else begin
pow_max <= pow_max;
val_max <= val_max;
val_min <= val_min;
pow_dif <= pow_dif;
en_dly0 <= 'd0;
end
end
//移位忙指示信号
reg shift_busy;
reg [4:0] shift_cnt;
always @(posedge clk or negedge rst_n) begin
if (rst_n==0) begin
shift_busy<='d0;
end
else if(en_dly0 == 1 )begin
shift_busy <='d1;
end
else if(shift_cnt == pow_dif)begin
shift_busy <= 0;
end
end
//移位计数
always @(posedge clk or negedge rst_n) begin
if(rst_n == 0)begin
shift_cnt <= 'd0;
end
else if (shift_busy ==1) begin
if (shift_cnt == pow_dif) begin
shift_cnt <= shift_cnt;
end
else begin
shift_cnt <= shift_cnt + 1'b1;
end
end
else begin
shift_cnt <= 'd0;
end
end
reg [22:0] val_shift;
always @(posedge clk or negedge rst_n) begin
if(rst_n == 0)begin
val_shift <= 'd0;
end
else if (en_dly0==1'b1) begin
val_shift <= val_min;
end
else if (shift_busy == 1) begin
val_shift <= {1'b0,val_shift[22:1]};
end
else begin
val_shift <= val_shift;
end
end
//尾数求和
wire val_add_flag = (shift_cnt == pow_dif)&&(shift_busy ==1);
reg [23:0] val_sum;
reg val_sum_vld;
always @(posedge clk or negedge rst_n) begin
if (rst_n==0) begin
val_sum<='d0;
val_sum_vld<='d0;
end
else if(val_add_flag == 1)begin
val_sum <= val_max + val_shift;
val_sum_vld<='d1;
end
else begin
val_sum <= val_sum;
val_sum_vld<='d0;
end
end
//规范
always @(posedge clk or negedge rst_n) begin
if (rst_n==0) begin
out<='d0;
out_vld<='d0;
end
else if(val_sum_vld == 1)begin
//尾数求和有溢出
out_vld<='d1;
out[31]<= signal_bit;
if(val_sum[23] == 1 && out[30:23] == 8'hFF)begin
out[30:23]<= 8'hFF;
out[22:0] <= 23'h7F_FFFF;
end
else if(val_sum[23] == 1)begin
out[30:23]<= pow_max + 1;
out[22:0] <= val_sum[23:1];
end
else begin
out[30:23]<= pow_max;
out[22:0] <= val_sum[22:0];
end
end
else begin
out <= out;
out_vld<='d0;
end
end
//运算忙指示
always @(posedge clk or negedge rst_n) begin
if (rst_n==0) begin
busy<='d0;
end
else if(en == 1 && busy == 0)begin
busy<='d1;
end
else if(out_vld == 1 )begin
busy<='d0;
end
else begin
busy <= busy;
end
end
endmodule
仿真代码
这里简单测试了下代码的功能,interwetten与威廉的赔率体系 了连续输入多个数据,核查是否数据会影响正常计算过程。
`timescale 1ns/1ps
module float_adder_tb;
// Parameters
// Ports
reg clk = 1;
reg rst_n = 0;
reg en = 0;
reg [31:0] aIn;
reg [31:0] bIn;
wire busy;
wire out_vld;
wire [31:0] out;
float_adder float_adder_dut (
.clk (clk ),
.rst_n (rst_n ),
.en (en ),
.aIn (aIn ),
.bIn (bIn ),
.busy (busy ),
.out_vld (out_vld ),
.out ( out)
);
always
#5 clk = ! clk ;
initial begin
rst_n = 0;
#100;
rst_n = 1;
#100;
aIn = {1'b0,8'd2,23'd7};
bIn = {1'b0,8'd2,23'd8};
en = 1 ;
#10;
aIn = {1'b0,8'd0,23'd7};
bIn = {1'b0,8'd2,23'd8};
en = 1 ;
#1000;
$finish;
end
endmodule
仿真测试
从仿真测试中可以看出,当输入信号连续输入两个浮点数时,在busy拉高状态下,第二次输入的数据无效,数据使能信号常为1,也不会影响正常模块运算过程,只有在该次运算完成busy拉低后数据可重新加载。
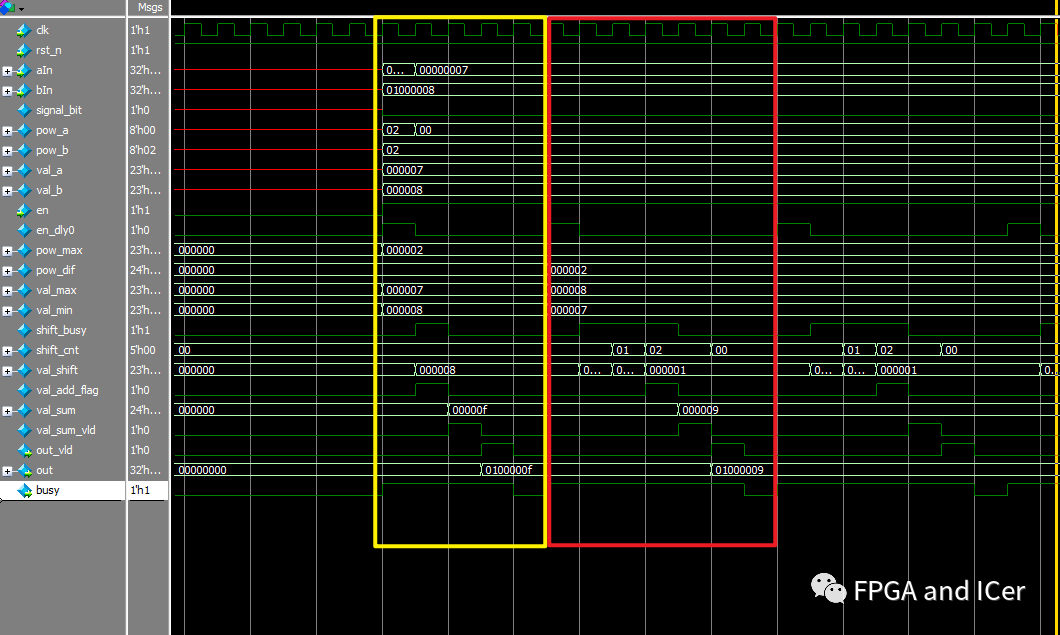 仿真截图
仿真截图小结
本文的设计方法对于对阶移位的操作需要循环操作,也即当阶数相差较小时,结果输出延迟较小,在极端情况下,比如阶数差大于10,输出延时会比阶数差为0时,多10个周期,上限为23。如在实际使用时,对延时要求较小的情况,可针对移位操作部分,使用更多的资源来换取性能的提升。可使用case语句对具体情况进行遍历。
针对原始题目中的累加操作,可将任意一个输入和输出相接,即可实现累加操作。此外,如果要实现异号加法情况,则需要仔细考虑对阶,规格化等情况进行进一步设计。
-
模块
+关注
关注
7文章
2696浏览量
47437 -
数据
+关注
关注
8文章
7006浏览量
88951 -
加法器
+关注
关注
6文章
183浏览量
30116
原文标题:小结
文章出处:【微信号:处芯积律,微信公众号:处芯积律】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
McASP采集这样的时序,是按照16bit采集,还是32bit采集?从Linux用户空间看,采集进来的数据是16bit还是32bit?
32bit MCU与16bit MCU的区别是什么
华邦针对SiP市场推出32bit SDR/DDR利基型内存
淘汰32bit不只iOS 11 明年开始扩展至Mac 32bit应用程序
32bit MCU 与 16bit MCU 的 区别

单片机里面“”32bit地址“”与所指向的“8bit数据“的关系

8bit 8051/32bit Cortex-M0 Flash单片机产品选型手册

RABPS 32bit by 3dmaniack 3dtoday (ARM BluePill Shield)已修复

使用STM32C0轻松实现从8bit到32bit的平台升级





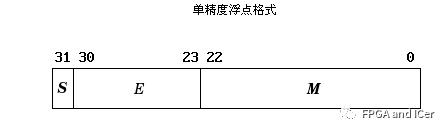
 32bit的浮点格式
32bit的浮点格式










评论