作者:John Dunn(EDN专栏作者) 编译:Anthea Chuang,EDN Taiwan 责编:Luffy Liu 本文来源EDN电子威廉希尔官方网站 设计
本文作者从他所知的高斯概率分布数学公式做出精彩的分析,最后导引到作为数学新手所经历的问题…许多人都是被教导如何使用数学大师们的努力成果,但是高斯如何得到他理论的结果?甚至其他大师们又是如何推论出伟大的定理?
这个interwetten与威廉的赔率体系
世界中的各种物理过程都表现出一定程度的随机性,例如,请想想噪声。高斯概率分布(Gaussian probability distributions)描述了许多噪声过程,我们应该看看它的数学公式。
从一个非常简单的公式开始,考虑高斯概率分布的“钟形曲线(bell curve)”公式: 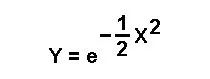
无需绘制图片,我们知道公式1所描述的曲线在x值为零时具有y值,并且我们进一步知道随着x值朝向任一值,y值都变为零,负无穷大或正无穷大。
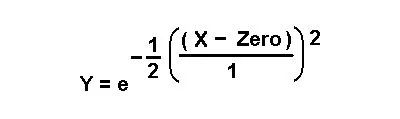
接下来,依照上面的公式添加“零”和数字“ 1”,这实际上并没有改变任何内容,但是会引导我们进行下一步。下面的公式3引入了平均值和标准偏差。
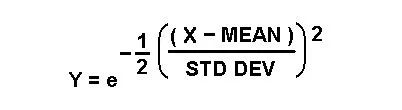
本文的“平均值”是一个新的中心值,围绕它的x值更改将影响y值。现在,当x值等于平均值时,y值将变为1,其中平均值可以为零,也可以为任何非零值。“标准偏差(standard deviation)”将影响随着x值偏离均值,y值向零下降的速度有多快。
标准偏差的较大值将要求x值与平均值相差很大,从而明显降低y值。另一方面,当标准偏差较小时,x值与均值的微小偏差将使y值更快地变为零。
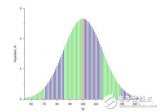
现在,绘制几张图片,以图形方式查看均值和标准偏差如何完成各自的工作(图1)。
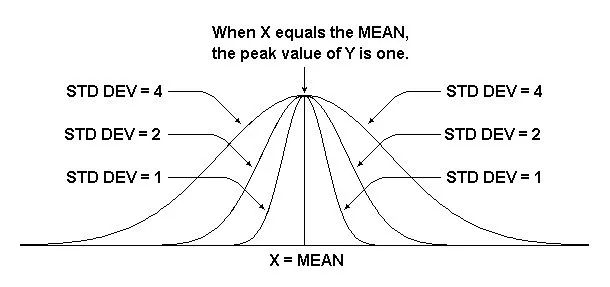
图1 显示平均值和标准偏差的影响。
接下来,透过标准偏差的倒数来缩放y值。请不要担心为何我们要这样做,请继续往下看。
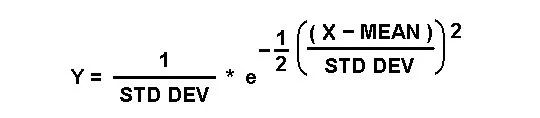
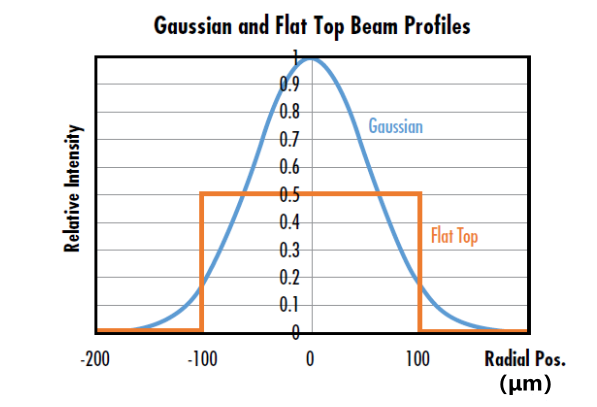
如果再仔细看一下图片,会看到标准偏差的附加影响(图2)。
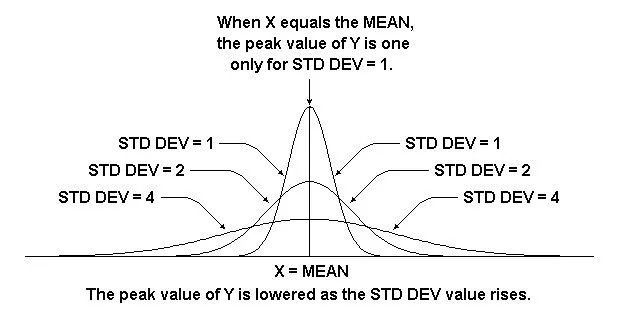
图2 显示标准偏差的附加影响。
接下来,输入另一个比例因子,即2 *π的平方根的倒数。再度呼吁,不用担心为什么,只要继续看下去。
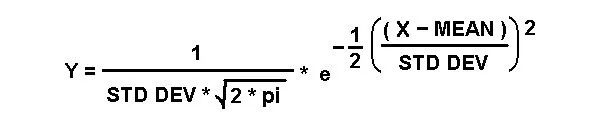
现在,导入一个称为“方差(variance)”的新术语。方差只是标准偏差的平方。可以将公式重写为: 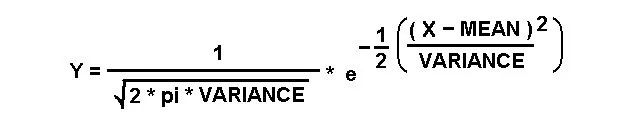
至此,我们已经完成了。如图2所示,如果针对从负无穷大到正无穷大的x值范围内的y值整合这最后两个公式中的任何一个并进行积分,则曲线下的面积等于1或等于1。使用我们进行的看似任意缩放,最后两个公式中的任何一个将产生一个积分结果。
无论你选择的是平均值、标准偏差还是方差,积分总是为1,这就是高斯概率分布,可以随意选择。
现在,我想谈谈作为数学新手所经历的一个问题。我试着理解卡尔·弗里德里希·高斯(Carl Friedrich Gauss)等如此伟大大师的作品。然而高斯工作时,纯粹是行动上的智慧。
他推断出上述公式中需要2 *π的平方根,但是高斯如何得出他的结果?我从未见过任何关于这方面的解释,也从未见过关于罗必达(l’Hospital)如何得出他寻找极限规则的任何解释,也没有见过关于帕普斯(Pappus)理论中寻找环形物体积或其他定理的任何解释。我只是被教导了这些天才努力的最终结果,以及如何应用其结果,仅此而已。 不知何故,由于缺乏更深层的解释,因此我觉得被哄骗。
审核编辑:刘清
-
积分器
+关注
关注
4文章
100浏览量
28447
原文标题:聊聊高斯概率分布的数学公式
文章出处:【微信号:光电读书,微信公众号:光电读书】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
紧急求教:高斯拟合如何求函数中心
一文了解高斯滤波器,附原理及实现过程
高斯过程回归GPR和多任务高斯过程MTGP
FOC有哪些数学公式
LTspice中使用蒙特卡罗和高斯分布进行容差分析和最差情况分析的方法
基于多高斯分布的背景生成算法
正态分布和高斯分布的作用_高斯分布的定义_误差服从高斯分布
多用户调度的高斯传输信道优化算法
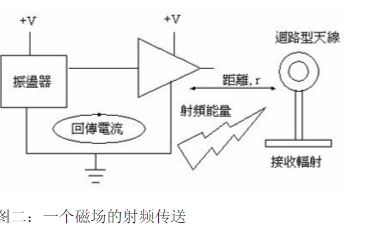
由数学公式和电磁理论分析PCB产品的特性和原理
图像高斯滤波的原理及FPGA实现思路





 高斯如何得到他理论的结果?聊聊高斯概率分布的数学公式
高斯如何得到他理论的结果?聊聊高斯概率分布的数学公式











评论