遗传算法是一种搜索算法,通过interwetten与威廉的赔率体系 自然界生物进化过程中遗传和适应性的机制,从多个解中寻找最优解。在置换流水车间调度问题中,可以使用遗传算法来求解最优解。
基于matlab实现遗传算法求解置换流水车间调度问题的步骤如下:
1.表示个体:将每个调度方案视为一个个体,用一个0~9的排列(即置换)表示工件的加工顺序;
2.初始群体:随机生成一定数量的个体作为初始群体;
3.适应度函数:定义一个适应度函数,该函数的输入是一个调度方案,输出是该方案的加工时间(即完成整个生产线加工的最短时间);
4.选择操作:通过轮盘赌等方式,从当前群体中选出一定数量的个体进入下一代群体;
5.交叉操作:对已选出的个体进行交叉,生成新的子代个体;
6.变异操作:对子代个体进行变异,以增加遗传多样性;
7.替换操作:将父代和子代个体合并,通过选择策略将一部分个体留下,另外的淘汰掉,留下的个体形成下一代群体,回到第4步进行下一轮演化。
在matlab中,可以使用遗传算法工具箱来实现上述步骤,详细操作可参考matlab官方文档或相关教材。需要注意的是,在编写适应度函数时,应考虑到生产线上的所有约束条件,如工序顺序、机器加工能力等,以确保求解出的调度方案符合实际生产需要。
遗传算法的数学公式原理
遗传算法是一种基于生物进化方法的优化算法,它通过模拟“基因、染色体、适应度、进化”等生物学概念,来解决各种优化问题。
在求解置换流水车间调度问题时,可以将每个工件看作是染色体的一个基因,每个工件的处理顺序表示染色体的排列方式,通过不断地交叉、变异和选择操作,逐步优化染色体的排列顺序,最终得到一个全局最优解。
具体地,遗传算法的数学公式原理如下:
初始化种群
在置换流水车间调度问题中,我们需要将工件以随机顺序分配给各个机器,这样生成的随机序列就是初始种群。
计算适应度
适应度函数用于评价染色体的优劣程度,通常指被优化的目标函数。对于置换流水车间调度问题,我们可以使用最后一个工件在最后一台机器上的完成时间作为适应度值。
选择操作
选择操作根据各个染色体的适应度值,按照一定的概率选择优秀的染色体作为下一代的父代染色体。常见的选择策略有轮盘赌选择、锦标赛选择等。
交叉操作
交叉操作模拟自然界的基因重组过程,通过随机选择两个父代染色体,按照一定的概率进行交叉操作,将两个染色体中的一部分基因进行交换,生成新的子代染色体。
变异操作
变异操作模拟自然界的基因突变过程,通过随机选择一个染色体,按照一定的概率对某一个基因进行随机变换,以增加搜索空间的广度。
更新种群
通过选择、交叉和变异操作,更新当前种群,进入下一代的迭代过程。
终止条件
当达到预定的迭代次数或者找到满足要求的最优解时,算法停止迭代。最后输出最优解和适应度值。
以上就是遗传算法求解置换流水车间调度问题的数学公式原理。其中,适应度函数、选择策略、交叉操作、变异操作等具体实现方法需要根据具体问题进行修改和优化。
代码实现
下面是基于 Matlab 实现遗传算法求解置换流水车间调度问题的简单代码实现。注意:本代码仅供参考,实际应用需要根据具体问题进行修改和优化。
clc clear %% 读取输入数据 job_num = 4; % 工件数 machine_num = 3; % 机器数 processing_time = [2 3 4; 3 1 6; 5 4 2; 1 3 4]; % 加工时间,矩阵第 i 行第 j 列表示第 i 个工件在第 j 台机器上的加工时间 %% 遗传算法参数设置 pop_size = 10; % 种群大小 max_gen = 100; % 最大迭代次数 pc = 0.8; % 交叉概率 pm = 0.2; % 变异概率 %% 初始化种群 pop = zeros(pop_size, job_num); for i = 1:pop_size pop(i,:) = randperm(job_num); end %% 开始迭代 for gen = 1:max_gen % 计算适应度 fitness = zeros(pop_size,1); for i = 1:pop_size fitness(i) = calc_fitness(pop(i,:), processing_time, machine_num); end % 选择操作 new_pop = zeros(pop_size, job_num); for i = 1:pop_size parent1 = select(pop, fitness); parent2 = select(pop, fitness); child = crossover(parent1, parent2, pc); new_pop(i,:) = child; end % 变异操作 for i = 1:pop_size new_pop(i,:) = mutate(new_pop(i,:), pm); end % 更新种群 pop = new_pop; end %% 输出结果 best_idx = find(fitness==min(fitness)); best_ind = pop(best_idx,:); best_fitness = fitness(best_idx); disp(['Best individual: ', num2str(best_ind)]); disp(['Best fitness: ', num2str(best_fitness)]); %% 计算适应度函数 function [fitness] = calc_fitness(chromosome, processing_time, machine_num) job_num = size(chromosome,2); T = zeros(job_num, machine_num); % 记录每个工件在每台机器上的完成时间 T(1,:) = processing_time(chromosome(1),:); for i = 2:job_num T(i,1) = T(i-1,1) + processing_time(chromosome(i),1); end for j = 2:machine_num T(1,j) = T(1,j-1) + processing_time(chromosome(1),j); end for i = 2:job_num for j = 2:machine_num T(i,j) = max(T(i-1,j), T(i,j-1)) + processing_time(chromosome(i),j); end end fitness = max(T(job_num,:)); % 最后一个工件在最后一台机器上的完成时间即为适应度 end %% 选择操作 function [parent] = select(pop, fitness) N = size(pop,1); idx1 = randi([1,N]); idx2 = randi([1,N]); if fitness(idx1) < fitness(idx2) parent = pop(idx1,:); else parent = pop(idx2,:); end end %% 交叉操作 function [child] = crossover(parent1, parent2, pc) job_num = size(parent1,2); child = zeros(1, job_num); if rand() < pc pos = randi([1,job_num-1]); % 随机选择交叉点 child(1:pos) = parent1(1:pos); for i = pos+1:job_num if ~ismember(parent2(i), child) % 确保每个工件只会被选取一次 child(i) = parent2(i); else j = 1; while true if ~ismember(parent2(j), child) child(i) = parent2(j); break end j = j + 1; end end end else child = parent1; end end %% 变异操作 function [mutant] = mutate(individual, pm) job_num = size(individual,2); mutant = individual; if rand() < pm pos1 = randi([1,job_num]); pos2 = randi([1,job_num]); mutant([pos1,pos2]) = mutant([pos2,pos1]); % 交换两个位置上的工件 end end
在这段代码中,calc_fitness 函数用于计算染色体的适应度值,select 函数用于选择父代染色体,crossover 函数用于进行交叉操作,mutate 函数用于进行变异操作。具体实现方法和参数设置可以参考注释部分。
-
matlab
+关注
关注
185文章
2974浏览量
230405 -
算法
+关注
关注
23文章
4608浏览量
92844 -
函数
+关注
关注
3文章
4329浏览量
62575
原文标题:【车间调度】基于matlab遗传算法求解置换流水车间调度问题
文章出处:【微信号:嵌入式职场,微信公众号:嵌入式职场】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
遗传算法置换流水车间调度目标函数建模问题(跪求!)
一种求解单件车间调度问题的单亲遗传算法
基于遗传算法的PID 控制及其MATLAB 仿真
资源限制混合流水车间调度的启发式算法
基于模拟退火遗传算法的多项目调度问题研究
基于遗传算法的战时备件配送车辆调度
车间作业调度问题遗传算法Matlab源码程序
求解DEC-POMDP问题的改进遗传算法

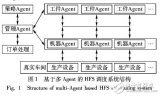
基于Agent的混合流水车间动态调度系统




 基于matlab遗传算法求解置换流水车间调度问题
基于matlab遗传算法求解置换流水车间调度问题










评论